R语言

随着大数据的概念变得越来越流行，对数据的探索、分析和挖掘已经成为大数据分析领域的基本技能之一。作为探索和分析数据的基本理论和工具，利用科学的数据挖掘技术进行数据预处理和借助成熟的数据挖掘算法进行模型拟合成为时下的热门技术之一。R语言作为功能强大并且免费的数据挖掘工具，在数据挖掘领域获得了越来越多用户的青睐。近几年，中国R语言大会在越来越多的城市举行，参会人数也呈现爆发式增长，尤其是业界人士占据了相当大的比例，R语言已成为企业界做数据分析挖掘必备的利器之一。

邓一硕写过一篇文章“R语言书籍的学习路线图”，很有参考意义，初级入门、高级入门、绘图与可视化、计量经济学、时间序列分析与金融等内容，涉及到30多本R语言书籍和小册子，但大部分都是英文的。
引用CSDN前辈的地址：https://blog.csdn.net/faith_binyang/article/details/79584655

CSDN上有两集免费的短介绍视频，其中推荐了一些学习方法：
中文书籍推荐：

R语言社区

R语言博客

操作：
养成好的习惯，首先更改目录。getwd()获得当前目录，setwd(" ")设定新的目录。
注释符号：#。
语句后面加分号（；）和MATLAB里面一样，是不显示该执行结果的意思。向上光标也是找回上一命令的意思。R中用（NA）表示缺失值。R中区分大小写，变量命名是用（字母、数字、句点）。寻求帮助用（？+函数名称）。
调用程序包：library(MASS以MASS为例)。
R中的与运算是（&）、或运算是（|）、非运算是（！）。
常见统计函数如下：

矩阵与数组：矩阵是特殊的数组。
矩阵：matrix；数组：array。
访问向量：x[i]；访问矩阵A[i,j]。
函数matrix( )用来创建矩阵。默认按列排列。矩阵的±*/^都是对其中各个元素。
函数array（）用来创建数组。

数据的读写
read.table（）：读表格形式的文件。
scan（）读纯文本格式文件。
绘图
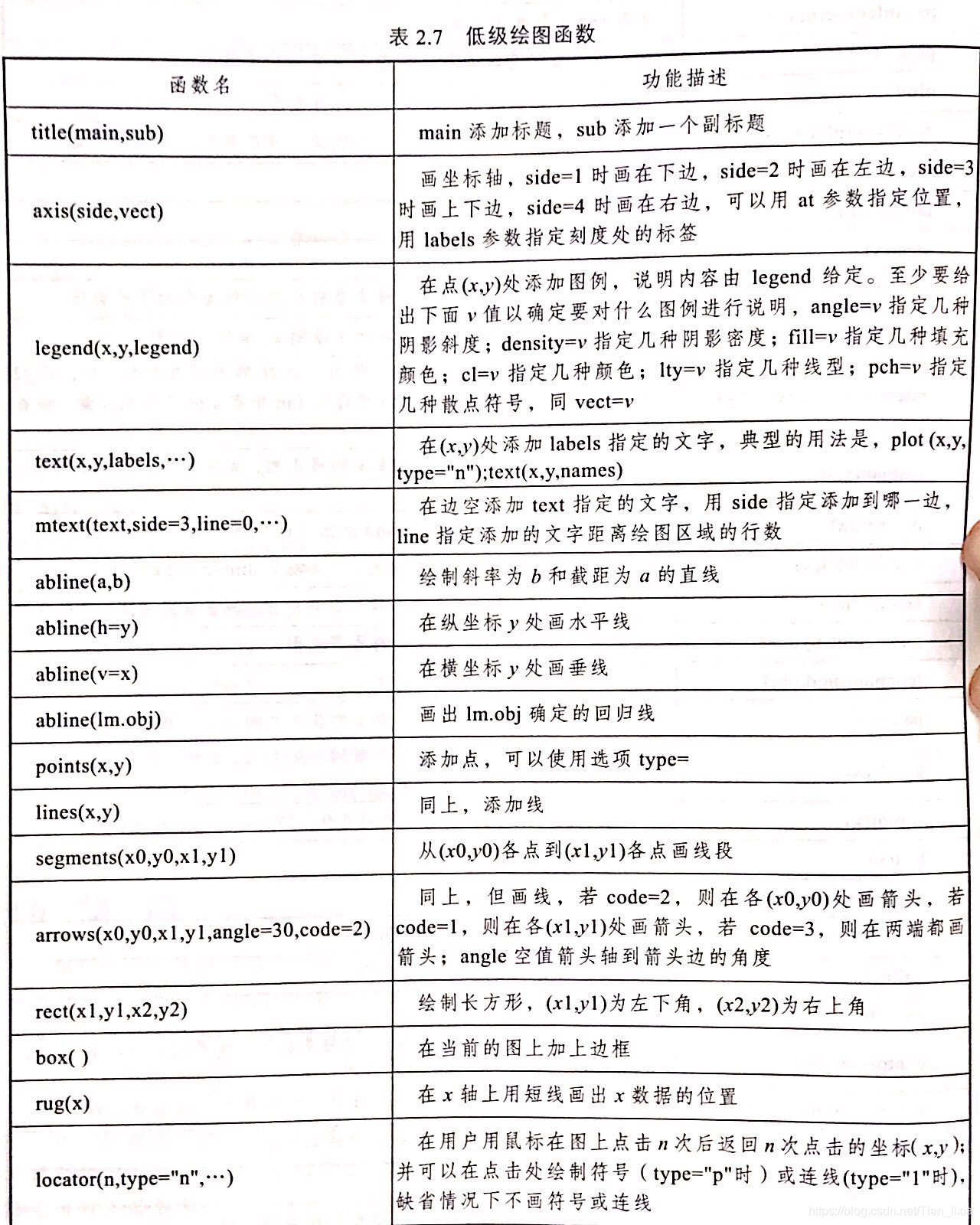
（1）高级绘图函数，创建一个新的图形，表2.6。
（2）低级绘图函数，在现存的图形上添加元素，表2.6。


箱形图：

参数检验与非参数检验
参数假设检验：事先假定总体的分布类型已知且都认为服从正态分布。
非参数检验：泛指“对分布类型已知的统计进行参数检验”之外的所有检验方法，对总体的分布进行假设，又叫拟合优度检验。
以下是非参数检验的几个方法：
（1）卡方检验（Chi-Square Test）：用于检验样本数据是否与某种概率分布的理论数值相符合，进而推断样本数据是否来自该分布的样本的问题。（原假设是不存在显著差异。概率p值小于显著水平α，拒绝原假设，即样本所属总体的分布与指定的理论分布存在显著差异；概率p值大于显著水平α，成立原假设，即样本所属总体的分布与指定的理论分布无显著差异；α一般为0.05）。R语言函数chisq.test（）。
（2）K-S检验：可利用样本数据推断总体是否服从某一理论分布。（原假设是不存在显著差异。概率p值小于显著水平α，拒绝原假设，即样本所属总体的分布与指定的理论分布存在显著差异；概率p值大于显著水平α，成立原假设，即样本所属总体的分布与指定的理论分布无显著差异；α一般为0.05）R语言函数ks.test（）。
（3）正态性的图检验：检验总体是否为正态分布。（因为很多统计方法中都假定样本来自正态总体，所以正态检验就很重要。原假设是…服从正态分布）QQ图法，qqnorm( )；qqline( )。

关联性检验
考察两个变量之间是否存在关系，例如研究肺癌与吸烟的关系，称为独立性检验。
1.卡方统计量，两个变量之间的相关程度。，观测值与期望值之间的接近程度，越接近，卡方值越小。
2.列联表检验
3.Fisher精确检验

蒙特卡罗

随机抽样方法，随机数的生成方法，利用蒙特卡罗方法解决积分问题，目前觉得这一部分我暂时用不到，所以暂时不整理。
第六章随机模拟实验、第七章随机过程计算与仿真也不整理。

方差分析与试验设计

单因素方差分析

在一项实验中，让一个因素的水平发生变化，其他因素水平保持不变，叫做单因素试验。处理单因素试验的统计推断问题称为单因素方差分析。


R语言中函数aov（）进行方差分析。函数summary（）可以列出方差分析表的详细结果。aov（）进行方差分析时需要进行正态性检验和方差一致性检验：命令shapiro.test（）是正态性检验，适用于样本容量n小于等于50时；命令bartlett.test（）是方差一致性检验。
另外，levene.test（）可以进行方差分析，适用于正态分布或非正态分布或分布不明的数据。
方差分析后的多重比较，就是进行方差分析得知了因子之间存在差异，想要知道具体哪些因子间存在差异，命令pairwise.t.test（）。

两因素等重复试验的方差分析

回归分析

变量间的统计关系：在统计推断中，把具有密切关系，但又不能由某一个或某一些变量唯一确定另外一个变量的关系，称为变量之间的统计关系或相关关系。
关于这个“统计关系”，现代统计学已经形成两个重要分支：相关关系和回归分析。

1.散点图：可以反映两个变量之间是否具有相关性，但不能体现相关强度。
2.相关系数：可以反映相关强度。叫做线性相关系数或Pearson相关系数。
多元线性回归分析：R^2。