同余定理:(a*b)%c == ((a%c)*b)%c == ((a%c * b%c)%c
证明(前一种): (a*b - a%c*b )为c的 倍数即可 提取b得到 b(a-a%c) 易知其为 c的 倍数 ,得证
一、一般的幂次取余 (主要利用(a*b)%c == ((a%c)*b)%c)
ll normal_mod(ll a, ll b, ll c){
ll ans = 1;
for(int i = 0; i < b; ++i){
ans = (ans*a)%c;//关键点
}
return ans;
}
二、介绍快速幂
快幂算法1
这里我们需要两个公式:
这两个公式都不难理解,自己可以验证一下,3^4 = 9^2。
有了这两个公式之后我们就可以考虑思路了。
我们就以b为偶数来举例。
a^b%c = ((a^2)^b/2)%c;
在这里我们假设b/2还是偶数,那么
((a^2)^b/2)%c = (((a^2)^2)^(b/2)/2)%c;到这里就可以了.
快速幂算法2
ll bin_pow(ll a, ll b){
ll ans = 1;
while((b&1) == 0){
b >>= 1;
a *= a;
}
while(b != 0){
if((b&1) == 1){
ans *= a;
}
a *= a;
b >>= 1;
}
return ans;
}
二、快速幂 + 取余
我们先将b按2进制展开假设b = 10, 那么b的二进制为1010,也就是0*2^0+1*2^1+0*2^2+1*2^3 = 10;
所以 a^b = a^(0*2^0+1*2^1+0*2^2+1*2^3 ) = a^(2^1) * a(2^3);这种简单的转换在初中就学过了吧,相信大家都懂
所以a^b%c = a^(2^1) * a(2^3) % c =( a^(2^1) % c) * (a(2^3)%c)%c;
ll pow_mod(ll a, ll b, ll c){
ll ans = 1;
while(b != 0){
if((b&1) == 1){
ans = (ans*a)%c;
}
b >>= 1;
a = (a*a)%c;
}
return ans;
}








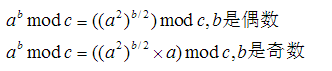














 764
764

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








