这篇文章介绍了ST-MoE(Stable and Transferable Mixture-of-Experts),一种设计稳定且可迁移的稀疏专家模型的方法。主要内容包括:
-
背景与动机:
-
稀疏专家模型(MoE)通过动态选择参数来处理输入,能够在保持计算量不变的情况下大幅扩展模型参数,提升效率。
-
然而,稀疏模型在训练和微调中存在不稳定性和质量不确定性的问题。
-
-
主要贡献:
-
提出了路由器z-loss,显著提高了训练稳定性,且不降低模型质量。
-
分析了稀疏模型和密集模型在微调中的不同超参数敏感性,发现稀疏模型需要更小的批大小和更高的学习率。
-
提出了稀疏模型的设计原则,包括专家数量、路由算法和容量因子的选择。
-
通过追踪token在模型中的路由,分析了编码器和解码器专家的专业化情况。
-
训练了一个2690亿参数的稀疏模型(ST-MoE-32B),在多个自然语言处理任务中实现了最先进的性能。
-
-
实验与结果:
-
在SuperGLUE、XSum、CNN-DM、ARC、WebQA等基准测试中,ST-MoE-32B表现优异,尤其在闭卷问答和对抗性任务上显著提升。
-
稀疏模型在大型任务上表现优于密集模型,但在小型任务上容易过拟合。
-
-
设计与优化:
-
推荐使用top-2路由和1.25容量因子,并建议每个核心使用不超过一个专家。
-
通过增加乘法交互和优化路由算法,进一步提升了模型性能。
-
-
未来工作:
-
探讨了稀疏模型在多语言数据上的不稳定性、自适应计算、低精度训练等方向的研究潜力。
-
ST-MoE通过改进训练稳定性、优化微调策略和设计高效的稀疏模型架构,显著提升了大规模语言模型的性能和实用性。这里是自己的论文阅读记录,感兴趣的话可以参考一下,如果需要阅读原文的话可以看这里,如下所示:

官方项目地址在这里,如下所示:
# coding=utf-8
# Copyright 2023 The Mesh TensorFlow Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Mixture-of-experts code.
Interfaces and algorithms are under development and subject to rapid change
without notice.
TODO(noam): Remove the other copy of this code from tensor2tensor.
TODO(noam): Write a new, simpler, cleaner version of this code.
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import gin
import mesh_tensorflow as mtf
from mesh_tensorflow.transformer import transformer
import tensorflow.compat.v1 as tf
@gin.configurable
class MoE1D(transformer.TransformerLayer):
"""Mixture of Experts Layer."""
def __init__(self,
num_experts=16,
loss_coef=1e-2,
hidden_size=4096,
group_size=1024,
capacity_factor_train=1.25,
capacity_factor_eval=2.0,
use_second_place_loss=False,
second_policy_train="random",
second_policy_eval="random",
second_threshold_train=0.2,
second_threshold_eval=0.2,
dropout_rate=0.0,
activation="relu",
moe_gating="top_2",
min_expert_capacity=4,
switch_policy_train="input_jitter",
switch_policy_eval="input_jitter",
switch_dropout=0.1,
switch_temperature=1.0,
switch_jitter=1e-2,
ntlb_top_k=4,
output_dim=None,
use_experts_attention=False,
z_loss=None,
word_embed_mode=None,
use_second_place_expert_prob=None,
use_second_place_expert_prob_temp=None,
top_n_num_experts_per_token=3):
self._hparams = HParams(
moe_gating=moe_gating,
moe_num_experts=num_experts,
moe_loss_coef=loss_coef,
moe_hidden_size=hidden_size,
moe_group_size=group_size,
moe_min_expert_capacity=min_expert_capacity,
moe_capacity_factor_train=capacity_factor_train,
moe_capacity_factor_eval=capacity_factor_eval,
moe_use_second_place_loss=use_second_place_loss,
moe_second_policy_train=second_policy_train,
moe_second_policy_eval=second_policy_eval,
moe_second_threshold_train=second_threshold_train,
moe_second_threshold_eval=second_threshold_eval,
moe_dropout_rate=dropout_rate,
moe_switch_policy_train=switch_policy_train,
moe_switch_policy_eval=switch_policy_eval,
moe_switch_dropout=switch_dropout,
moe_switch_temperature=switch_temperature,
moe_switch_jitter=switch_jitter,
moe_output_dim=output_dim,
moe_ntlb_top_k=ntlb_top_k,
moe_use_experts_attention=use_experts_attention,
moe_z_loss=z_loss,
moe_word_embed_mode=word_embed_mode,
moe_use_second_place_expert_prob=(
use_second_place_expert_prob),
moe_use_second_place_expert_prob_temp=(
use_second_place_expert_prob_temp),
moe_top_n_num_experts_per_token=top_n_num_experts_per_token)
self._activation = activation
def call(self, context, x, losses=None):
"""Call the layer."""
if context.model.ensemble_dim:
raise NotImplementedError("MoE not yet implemented with ensembles")
has_length_dim = context.length_dim in x.shape.dims
if not has_length_dim:
x_shape = x.shape
shape_with_length = mtf.Shape(
x_shape.dims[:-1] + [mtf.Dimension("length", 1)]
+ x_shape.dims[-1:])
x = mtf.reshape(x, shape_with_length)
# Extract the MoE output dimension
if self._hparams.moe_output_dim is not None:
output_dim = self._hparams.moe_output_dim
else:
output_dim = context.model.model_dim
y, loss = transformer_moe_layer_v1(
x,
output_dim,
self._hparams,
context.train,
context.variable_dtype,
layout=context.model.layout,
mesh_shape=context.model.mesh_shape,
nonpadding=context.nonpadding,
activation=self._activation,
num_microbatches=context.num_microbatches,
token_embeddings=context.input_embeddings)
if context.losses is not None:
context.losses.append(loss)
if not has_length_dim:
if self._hparams.moe_use_experts_attention:
y_reshape = [mtf.reshape(y_out, x_shape) for y_out in y]
y = y_reshape
else:
y = mtf.reshape(y, x_shape)
return y
class MoE2D(transformer.TransformerLayer):
"""Mixture of Experts Layer."""
def __init__(self,
expert_x=8,
expert_y=8,
loss_coef=1e-2,
hidden_size=4096,
group_size=1024,
capacity_factor_train=1.25,
capacity_factor_eval=2.0,
capacity_factor_second_level=1.0,
use_second_place_loss=False,
second_policy_train="random",
second_policy_eval="random",
second_threshold_train=0.2,
second_threshold_eval=0.2):
self._hparams = HParams(
moe_gating="top_2",
moe_num_experts=[expert_x, expert_y],
moe_loss_coef=loss_coef,
moe_hidden_size=hidden_size,
moe_group_size=group_size,
moe_capacity_factor_train=capacity_factor_train,
moe_capacity_factor_eval=capacity_factor_eval,
moe_capacity_factor_second_level=capacity_factor_second_level,
moe_use_second_place_loss=use_second_place_loss,
moe_second_policy_train=second_policy_train,
moe_second_policy_eval=second_policy_eval,
moe_second_threshold_train=second_threshold_train,
moe_second_threshold_eval=second_threshold_eval)
def call(self, context, x, losses=None):
"""Call the layer."""
if context.model.ensemble_dim:
raise NotImplementedError("MoE not yet implemented with ensembles")
has_length_dim = context.length_dim in x.shape.dims
if not has_length_dim:
x_shape = x.shape
shape_with_length = mtf.Shape(
x_shape.dims[:-1] + [mtf.Dimension("length", 1)]
+ x_shape.dims[-1:])
x = mtf.reshape(x, shape_with_length)
y, loss = transformer_moe_layer_v2(
x,
context.model.model_dim,
self._hparams,
context.train,
context.variable_dtype,
layout=context.model.layout,
mesh_shape=context.model.mesh_shape,
nonpadding=context.nonpadding,
num_microbatches=context.num_microbatches)
if context.losses is not None:
context.losses.append(loss)
if not has_length_dim:
y = mtf.reshape(y, x_shape)
return y
def transformer_moe_layer_v1(
inputs, output_dim, hparams, train, variable_dtype,
layout=None, mesh_shape=None, nonpadding=None, activation=mtf.relu,
num_microbatches=None, token_embeddings=None):
"""Local mixture of experts that works well on TPU.
Adapted from the paper https://arxiv.org/abs/1701.06538
Note: until the algorithm and inferface solidify, we pass in a hyperparameters
dictionary in order not to complicate the interface in mtf_transformer.py .
Once this code moves out of "research", we should pass the hyperparameters
separately.
Hyperparameters used:
hparams.moe_num_experts: number of experts
hparams.moe_hidden_size: size of hidden layer in each expert
hparams.moe_group_size: size of each "group" for gating purposes
hparams.moe_capacity_factor_train: a float
hparams.moe_capacity_factor_eval: a float
hparams.moe_gating: a string
+ all hyperparmeters used by _top_2_gating()
The number of parameters in the gating network is:
(input_dim.size * hparams.num_experts) +
The number of parameters in the experts themselves is:
(hparams.num_experts
* (input_dim.size + output_dim.size)
* hparams.moe_hidden_size)
The input is n-dimensional: [<batch_and_length_dims>, input_dim], consisting
of the representations of all positions in a batch of sequences.
Each position of each sequence is sent to 0-2 experts. The expert
choices and the combination weights are determined by a learned gating
function.
This function returns a small auxiliary loss that should be added to the
training loss of the model. This loss helps to balance expert usage.
Without the loss, it is very likely that a few experts will be trained and
the rest will starve.
Several hacks are necessary to get around current TPU limitations:
- To ensure static shapes, we enforce (by truncation/padding)
that each sequence send the same number of elements to each expert.
It would make more sense to enforce this equality over the entire batch,
but due to our hacked-up gather-by-matmul implementation, we need to divide
the batch into "groups". For each group, the same number of elements
are sent to each expert.
TODO(noam): Factor this code better. We want to be able to substitute
different code for the experts themselves.
Dimensions cheat sheet:
B: batch dim(s)
L: original sequence length
M: input depth
N: output depth
G: number of groups
S: group size
E: number of experts
C: expert capacity
Args:
inputs: a mtf.Tensor with shape [batch_dim(s), length_dim, input_dim]
output_dim: a mtf.Dimension (for Transformer, this is input_dim)
hparams: model hyperparameters
train: a boolean
variable_dtype: a mtf.VariableDType
layout: optional - an input to mtf.convert_to_layout_rules
mesh_shape: optional - an input to mtf.convert_to_shape
nonpadding: an optional Tensor with shape [batch_dim(s), length_dim]
and the same dtype as inputs, consisting of ones(nonpadding)
and zeros(padding).
activation: a function.
num_microbatches: number of microbatches.
token_embeddings: a mtf.Tensor with shape
[batch_dim(s), length_dim, input_dim]. These are the word embeddings for
that correspond to the inputs. These can optionally be used to make
routing decisions.
Returns:
outputs: a Tensor with shape [batch_dim(s), length_dim, output_dim]
loss: a mtf scalar
Raises:
ValueError: on unrecognized hparams.moe_gating
"""
# pylint: disable=line-too-long
#
# O outer_batch dimension can be used for expert replication, e.g.
# outer_batch=4 for placing 128 experts on 512 cores with 4 replicas of each
# expert.
#
# E.g. 16x16 basic example:
# moe_num_experts=512, num_groups=1024, batch=4096, length=256, d_model=1024
# ---
# Below ` indicates common way of splitting along mesh dimension.
#
# orig_inputs OB`LM Tensor
# Shape[outer_batch=1, batch=4096, length=256, d_model=1024]
# v (reshaped)
# inputs OG`SM
# Shape[outer_batch=1, batch=1024, group=1024, d_model=1024]
#
# combine_tensor,
# dispatch_tensor OG`SEC
# Shape[outer_batch=1, batch=1024, group=1024, expert_unsplit=512, expert_capacity=4]
#
# (dispatched inputs)
# expert_inputs OEG`CM
# Shape[outer_batch=1, expert_unsplit=512, batch=1024, expert_capacity=4, d_model=1024]
# v (re-split via ReshapeOperation)
# OE`GCM
# Shape[outer_batch=1, experts=512, batch_unsplit=1024, expert_capacity=4, d_model=1024]
#
# (hidden representation)
# h OE`GCH
# Shape[outer_batch=1, experts=512, batch_unsplit=1024, expert_capacity=4, expert_hidden=8192]
#
# expert_output OE`GCM
# Shape[outer_batch=1, experts=512, batch_unsplit=1024, expert_capacity=4, d_model=1024]
# v (re-split via ReshapeOperation)
# OEG`CM
# Shape[outer_batch=1, expert_unsplit=512, batch=1024, expert_capacity=4, d_model=1024]
#
# (combined expert_output)
# output OG`SM
# Shape[outer_batch=1, batch=1024, group=1024, d_model=1024
# v (reshape)
# OB`LM
# Shape[outer_batch=1, batch=4096, length=256, d_model=1024]
#
# pylint: enable=line-too-long
orig_inputs = inputs
hidden_dim = mtf.Dimension("expert_hidden", hparams.moe_hidden_size)
experts_dim = mtf.Dimension("experts", hparams.moe_num_experts)
# We "cheat" here and look at the mesh shape and layout. This is to ensure
# that the number of groups is a multiple of the mesh dimension
# over which those groups are split.
batch_and_length_dims, input_dim = (orig_inputs.shape.dims[:-1],
orig_inputs.shape.dims[-1])
# Hack: we assume that
# "outer_batch" == replication of experts
# mesh_dim_size can be derived from mesh_shape and orig_batch_dim
#
# We then reqire num_groups to be a multiple of mesh_dim_size.
if orig_inputs.shape.dims[0].name == "outer_batch":
outer_batch_dim, orig_batch_dim = orig_inputs.shape.dims[:2]
else:
outer_batch_dim, orig_batch_dim = (mtf.Dimension("outer_batch", 1),
orig_inputs.shape.dims[0])
# Number of MoE inputs (total number of position across batch_and_length_dims
# per replica.
n = 1
for d in batch_and_length_dims:
n *= d.size
n = n // outer_batch_dim.size
mesh_dim_size = mtf.tensor_dim_to_mesh_dim_size(layout, mesh_shape,
orig_batch_dim)
num_groups, group_size = _split_into_groups(n, hparams.moe_group_size,
mesh_dim_size)
group_size_dim = mtf.Dimension("group", group_size)
num_groups_dim = mtf.Dimension(orig_batch_dim.name, num_groups)
moe_input_dims = [outer_batch_dim, num_groups_dim, group_size_dim, input_dim]
# OGSM Tensor
inputs = mtf.reshape(inputs, moe_input_dims)
# Token embeddings that can be optionally used in the router for determining
# where to send tokens.
if hparams.moe_word_embed_mode is not None:
token_embeddings = mtf.cast(
mtf.reshape(token_embeddings, moe_input_dims), inputs.dtype)
# Each sequence sends expert_capacity positions to each expert.
if train:
capacity_factor = hparams.moe_capacity_factor_train
else:
capacity_factor = hparams.moe_capacity_factor_eval
expert_capacity = min(
group_size_dim.size,
int((group_size_dim.size * capacity_factor) / experts_dim.size))
expert_capacity = max(expert_capacity, hparams.moe_min_expert_capacity)
tf.logging.info("expert_capacity: %d" % expert_capacity)
expert_capacity_dim = mtf.Dimension("expert_capacity", expert_capacity)
experts_dim_unsplit = mtf.Dimension("expert_unsplit", experts_dim.size)
batch_dim_unsplit = mtf.Dimension("batch_unsplit", num_groups_dim.size)
if nonpadding is not None:
nonpadding = mtf.zeros(
inputs.mesh, batch_and_length_dims, dtype=inputs.dtype) + nonpadding
nonpadding = mtf.reshape(nonpadding, moe_input_dims[:-1])
if hparams.moe_gating == "top_2":
# combine_tensor,
# dispatch_tensor OG`SEC Tensors
# (G is generally split along mesh dim)
dispatch_tensor, combine_tensor, loss = _top_2_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=experts_dim_unsplit,
expert_capacity_dim=expert_capacity_dim,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=nonpadding,
num_microbatches=num_microbatches,
token_embeddings=token_embeddings)
elif hparams.moe_gating == "top_n":
dispatch_tensor, combine_tensor, loss = _top_n_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=experts_dim_unsplit,
expert_capacity_dim=expert_capacity_dim,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=nonpadding,
num_microbatches=num_microbatches,
token_embeddings=token_embeddings)
elif hparams.moe_gating == "switch":
dispatch_tensor, combine_tensor, loss = _switch_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=experts_dim_unsplit,
expert_capacity_dim=expert_capacity_dim,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=nonpadding,
num_microbatches=num_microbatches,
token_embeddings=token_embeddings)
elif hparams.moe_gating == "ntlb":
dispatch_tensor, combine_tensor, loss = _ntlb_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=experts_dim_unsplit,
expert_capacity_dim=expert_capacity_dim,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=nonpadding,
num_microbatches=num_microbatches,
token_embeddings=token_embeddings)
elif hparams.moe_gating == "switch_max":
dispatch_tensor, combine_tensor, loss = _switch_max_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=experts_dim_unsplit,
expert_capacity_dim=expert_capacity_dim,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=nonpadding,
num_microbatches=num_microbatches,
token_embeddings=token_embeddings)
elif hparams.moe_gating == "expert_selection":
dispatch_tensor, combine_tensor, loss = _expert_selection_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=experts_dim_unsplit,
group_size_dim=group_size_dim,
expert_capacity_dim=expert_capacity_dim,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=nonpadding,
name="expert_selection_gating",
num_microbatches=num_microbatches,
token_embeddings=token_embeddings)
else:
raise ValueError("unknown hparams.moe_gating=%s" % hparams.moe_gating)
expert_inputs = mtf.einsum([inputs, dispatch_tensor],
mtf.Shape([
outer_batch_dim, experts_dim_unsplit,
num_groups_dim, expert_capacity_dim, input_dim
]))
# Extra reshape reduces communication cost for model-parallel versions.
# For model-parallel versions, this reshape causes an mtf.slice and for non-
# model-parallel versions, this has no effect.
d_model_split_dim = mtf.Dimension("d_model_split", input_dim.size)
expert_inputs = mtf.reshape(
expert_inputs,
mtf.Shape([
outer_batch_dim, experts_dim, batch_dim_unsplit, expert_capacity_dim,
d_model_split_dim
]))
# Split over batch -> split over experts
expert_inputs = mtf.reshape(
expert_inputs,
mtf.Shape([
outer_batch_dim, experts_dim, batch_dim_unsplit, expert_capacity_dim,
input_dim
]))
# Now feed the expert inputs through the experts.
h = mtf.layers.dense_product(
expert_inputs,
reduced_dims=expert_inputs.shape.dims[-1:],
new_dims=[hidden_dim],
expert_dims=[experts_dim],
activation_functions=activation, use_bias=False,
variable_dtype=variable_dtype, name="wi")
if hparams.moe_dropout_rate != 0.0:
h = mtf.dropout(h, is_training=train,
keep_prob=1.0 - hparams.moe_dropout_rate)
def _compute_output(hidden, layer_name):
"""Compute the output of the attention layer from the hidden vector."""
expert_output = mtf.layers.dense(
hidden, output_dim, expert_dims=[experts_dim], use_bias=False,
reduced_dims=hidden.shape.dims[-1:], variable_dtype=variable_dtype,
name=layer_name)
# Extra reshape reduces communication cost for model-parallel versions.
# For model-parallel versions, this reshape causes an mtf.slice and for non-
# model-parallel versions, this has no effect.
d_model_split_dim = mtf.Dimension(
"d_model_split", expert_output.shape[-1].size)
expert_output = mtf.reshape(
expert_output,
mtf.Shape([
outer_batch_dim, experts_dim_unsplit, num_groups_dim,
expert_capacity_dim, d_model_split_dim
]))
# Split over experts -> split over batch
expert_output = mtf.reshape(
expert_output,
mtf.Shape([
outer_batch_dim,
experts_dim_unsplit,
num_groups_dim,
expert_capacity_dim,
output_dim,
]))
moe_output_dims = moe_input_dims[:-1] + [output_dim]
output = mtf.einsum([expert_output, combine_tensor],
mtf.Shape(moe_output_dims))
output = mtf.reshape(output, batch_and_length_dims + [output_dim])
return output
if hparams.moe_use_experts_attention:
# We share k_h and v_h with no degradation in performance
q_h, k_h = h, h
outputs = []
q = _compute_output(q_h, layer_name="q_wo")
k = _compute_output(k_h, layer_name="k_wo")
outputs.append(q)
outputs.append(k)
return outputs, loss * hparams.moe_loss_coef
else:
output = _compute_output(h, layer_name="wo")
return output, loss * hparams.moe_loss_coef
def transformer_moe_layer_v2(
inputs, output_dim, hparams, train, variable_dtype,
layout=None, mesh_shape=None, nonpadding=None, num_microbatches=None):
"""2-level mixture of experts.
Adapted from the paper https://arxiv.org/abs/1701.06538
Note: until the algorithm and inferface solidify, we pass in a hyperparameters
dictionary in order not to complicate the interface in mtf_transformer.py .
Once this code moves out of "research", we should pass the hyperparameters
separately.
Hyperparameters used:
hparams.moe_num_experts: number of experts
hparams.moe_hidden_size: size of hidden layer in each expert
hparams.moe_group_size: size of each "group" for gating purposes
hparams.moe_capacity_factor_train: a float
hparams.moe_capacity_factor_eval: a float
hparams.moe_capacity_factor_second_level: a float
hparams.moe_gating: a string
+ all hyperparmeters used by _top_2_gating()
One set of params for experts in first level and different of hparams
per expert in the second level.
The number of parameters in the gating network is:
(input_dim.size * (hparams.num_experts) +
(moe_hidden_size * hparams.num_experts) * hparams.num_experts
The number of parameters in the experts themselves is:
(hparams.num_experts
* (input_dim.size + output_dim.size)
* hparams.moe_hidden_size)
The input is n-dimensional: [<batch_and_length_dims>, input_dim], consisting
of the representations of all positions in a batch of sequences.
Each position of each sequence is sent to 0-3 experts. The expert
choices and the combination weights are determined by a learned gating
function.
This function returns a small auxiliary loss that should be added to the
training loss of the model. This loss helps to balance expert usage.
Without the loss, it is very likely that a few experts will be trained and
the rest will starve.
Several hacks are necessary to get around current TPU limitations:
- To ensure static shapes, we enforce (by truncation/padding)
that each sequence send the same number of elements to each expert.
It would make more sense to enforce this equality over the entire batch,
but due to our hacked-up gather-by-matmul implementation, we need to divide
the batch into "groups". For each group, the same number of elements
are sent to each expert.
TODO(noam): Factor this code better. We want to be able to substitute
different code for the experts themselves.
Dimensions cheat sheet:
a, b: batch size
l: original sequence length
m: input depth
n: output depth
g, h: number of groups
s, t: group size
x, y: number of experts
c, d: expert capacity
input: [a0, b1, l, m]
input: [a0, g1, s, m]
dispatch_tensor_x: [a0, g1, s, x, c]
expert_input: [a0, g1, x, c, m]
alltoall: [a0, g, x1, c, m]
alltoall: [a0, g, x1, c, m]
transpose: [x1, a0, g, c, m]
reshape: [x1, h0, s, m]
assignment2: [x1, h0, t, y, d]
expert_input2: [x1, h0, y, d, m]
alltoall: [x1, h, y0, d, m]
...
reverse of that
gating params 0: [m, x]
gating params 1: [x1, m, y]
expert params:
[x1, y0, m, hidden]
[x1, y0, hidden, n]
Args:
inputs: a mtf.Tensor with shape [a, b, l, m]
output_dim: a mtf.Dimension (for Transformer, this is input_dim)
hparams: model hyperparameters
train: a boolean
variable_dtype: a mtf.VariableDType
layout: optional - an input to mtf.convert_to_layout_rules
mesh_shape: optional - an input to mtf.convert_to_shape
nonpadding: an optional mtf.Tensor with shape [a, b, l]
and the same dtype as inputs, consisting of ones(nonpadding)
and zeros(padding).
num_microbatches: number of microbatches.
Returns:
outputs: a Tensor with shape [a, b, l, n]
loss: a mtf scalar
Raises:
ValueError: on unrecognized hparams.moe_gating
"""
if nonpadding is not None:
nonpadding = mtf.zeros(inputs.mesh, inputs.shape.dims[:-1],
dtype=inputs.dtype) + nonpadding
insert_outer_batch_dim = (len(inputs.shape.dims) == 3)
if insert_outer_batch_dim:
inputs = mtf.reshape(
inputs, [mtf.Dimension("outer_batch", 1)] + inputs.shape.dims)
assert len(hparams.moe_num_experts) == 2
a0, b1, l, m = inputs.shape.dims
hidden_dim = mtf.Dimension("expert_hidden", hparams.moe_hidden_size)
x1 = mtf.Dimension("expert_x", hparams.moe_num_experts[0])
y0 = mtf.Dimension("expert_y", hparams.moe_num_experts[1])
x = mtf.Dimension("expert_x_unsplit", hparams.moe_num_experts[0])
y = mtf.Dimension("expert_y_unsplit", hparams.moe_num_experts[1])
n = output_dim
# We "cheat" here and look at the mesh shape and layout. This is to ensure
# that the number of groups (g.size) is a multiple of the mesh dimension
# over which those groups are split.
num_groups, group_size = _split_into_groups(
b1.size * l.size, hparams.moe_group_size,
mtf.tensor_dim_to_mesh_dim_size(layout, mesh_shape, b1))
g1 = mtf.Dimension(b1.name, num_groups)
g = mtf.Dimension(b1.name + "_unsplit", g1.size)
s = mtf.Dimension("group_size_x", group_size)
# Each sequence sends (at most?) expert_capacity positions to each expert.
# Static expert_capacity dimension is needed for expert batch sizes
if train:
capacity_factor = hparams.moe_capacity_factor_train
else:
capacity_factor = hparams.moe_capacity_factor_eval
expert_capacity = min(s.size, int((s.size * capacity_factor) / x.size))
expert_capacity = max(expert_capacity, hparams.moe_min_expert_capacity)
c = mtf.Dimension("expert_capacity_x", expert_capacity)
# We "cheat" here and look at the mesh shape and layout. This is to ensure
# that the number of groups (h.size) is a multiple of the mesh dimension
# over which those groups are split.
num_groups, group_size = _split_into_groups(
a0.size * g.size * c.size,
hparams.moe_group_size,
mtf.tensor_dim_to_mesh_dim_size(layout, mesh_shape, a0))
t = mtf.Dimension("group_size_y", group_size)
h0 = mtf.Dimension(a0.name, num_groups)
h = mtf.Dimension(a0.name + "_unsplit", h0.size)
expert_capacity = min(
t.size,
int((t.size * hparams.moe_capacity_factor_second_level) / y.size))
expert_capacity = max(expert_capacity, hparams.moe_min_expert_capacity)
d = mtf.Dimension("expert_capacity_y", expert_capacity)
# First level of expert routing
# Reshape the inner batch size to a multiple of group_dim g1 and
# group_size_dim s.
inputs = mtf.reshape(inputs, [a0, g1, s, m])
if nonpadding is not None:
nonpadding = mtf.reshape(nonpadding, [a0, g1, s])
# Get the assignments for the first level.
# dispatch_tensor_x has shape [a0, g1, s, x, c]
if hparams.moe_gating == "top_2":
dispatch_tensor_x, combine_tensor_x, loss_outer = _top_2_gating(
inputs=inputs,
outer_expert_dims=None,
experts_dim=x,
expert_capacity_dim=c,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
name="outer_gating",
importance=nonpadding,
num_microbatches=num_microbatches)
else:
raise ValueError("unknown hparams.moe_gating=%s" % hparams.moe_gating)
# Now create expert_inputs based on the assignments.
# put num_experts dimension first to make split easier in alltoall
expert_inputs_x = mtf.einsum([inputs, dispatch_tensor_x], [x, a0, g1, c, m])
# we construct an "importance" Tensor for the inputs to the second-level
# gating. The importance of an input is 1.0 if it represents the
# first-choice expert-group and 0.5 if it represents the second-choice expert
# group. This is used by the second-level gating.
importance = mtf.reduce_sum(combine_tensor_x, output_shape=[x, a0, g1, c])
importance = 0.5 * (
mtf.to_float(mtf.greater(importance, 0.5)) +
mtf.to_float(mtf.greater(importance, 0.0)))
# First level, all to all. Here we change the split dimension from g1 to x1.
expert_inputs_x = mtf.reshape(expert_inputs_x, mtf.Shape(
[x1, a0, g, c, m]))
importance = mtf.reshape(importance, [x1, a0, g, c])
# Second level of expert routing
# Reshape the expert_inputs outer batch dim to be a multiple of group_dim h0
# and group_size_dim t.
inputs_y = mtf.reshape(expert_inputs_x, [x1, h0, t, m])
importance = mtf.reshape(importance, [x1, h0, t])
# Get the assignments for the second level.
# dispatch_tensor_y has shape [x1, h0, t, y, d]
if hparams.moe_gating == "top_2":
dispatch_tensor_y, combine_tensor_y, loss_inner = _top_2_gating(
inputs=inputs_y,
outer_expert_dims=[x1],
experts_dim=y,
expert_capacity_dim=d,
hparams=hparams,
train=train,
variable_dtype=variable_dtype,
importance=importance,
name="inner_gating",
num_microbatches=num_microbatches)
else:
raise ValueError("unknown hparams.moe_gating=%s" % hparams.moe_gating)
# Now create expert_inputs based on the assignments.
# put num_experts dimension first to make split easier in alltoall
expert_inputs_y = mtf.einsum([inputs_y, dispatch_tensor_y], [y, x1, h0, d, m])
# Second level, all to all. Here we change the split dimension from h0 to y0.
expert_inputs_y = mtf.reshape(expert_inputs_y, mtf.Shape(
[y0, x1, h, d, m]))
hidden_output = mtf.layers.dense(
expert_inputs_y, hidden_dim, expert_dims=[y0, x1],
reduced_dims=expert_inputs_y.shape.dims[-1:],
activation=mtf.relu, use_bias=False, variable_dtype=variable_dtype,
name="wi")
expert_output = mtf.layers.dense(
hidden_output, output_dim, expert_dims=[y0, x1],
reduced_dims=hidden_output.shape.dims[-1:],
use_bias=False, variable_dtype=variable_dtype,
name="wo")
# NOW COMBINE EXPERT OUTPUTS (reversing everything we have done)
# expert_output has shape [y0, x1, h, d, n]
# alltoall
expert_output = mtf.reshape(expert_output, mtf.Shape(
[y, x1, h0, d, n]))
# combine results from inner level
output_y = mtf.einsum([expert_output, combine_tensor_y], [x1, h0, t, n])
# Reshape the combined tensor from inner level to now contain outer_batch_dim
# a0 and group_dim g
output = mtf.reshape(output_y, [x1, a0, g, c, n])
# alltoall from expert_dim x to group_dim g1
expert_output_x = mtf.reshape(output, mtf.Shape([x, a0, g1, c, n]))
# combine results from outer level
output_x = mtf.einsum([expert_output_x, combine_tensor_x], [a0, g1, s, n])
# Reshape the combined tensor to now contain inner_batch_dim
# b1 and the original sequence length
output = mtf.reshape(output_x, [a0, b1, l, n])
if insert_outer_batch_dim:
output = mtf.reshape(output, [b1, l, n])
return output, (loss_outer + loss_inner) * hparams.moe_loss_coef
def _stochastically_use_non_top_expert(gate_logits, experts_dim, hparams):
"""With a specified probability use the second place or lower experts."""
# With the specified probability use the second place expert in place of the
# top expert.
tf.logging.info("Using second place expert with prob: {}".format(
hparams.moe_use_second_place_expert_prob))
_, top_expert_index = mtf.top_1(gate_logits, reduced_dim=experts_dim)
top_expert_mask = mtf.one_hot(
top_expert_index, experts_dim, dtype=gate_logits.dtype)
# With probability moe_expert_use_second_place_expert_prob send the token to
# the non-top expert.
use_second_place_expert = mtf.cast(
mtf.less(
mtf.random_uniform(gate_logits.mesh, gate_logits.shape[:-1]),
hparams.moe_use_second_place_expert_prob), gate_logits.dtype)
# Mask out the top logit.
second_place_gate_logits = -1e9 * top_expert_mask + gate_logits
# If a temperature is specified sample from the remaining N-1 experts.
if hparams.moe_use_second_place_expert_prob_temp is not None:
tf.logging.info("Expert second place temp: {}".format(
hparams.moe_use_second_place_expert_prob_temp))
# What expert should be used.
second_expert_index = mtf.sample_with_temperature(
second_place_gate_logits, experts_dim,
temperature=hparams.moe_use_second_place_expert_prob_temp)
second_expert_mask = mtf.one_hot(
second_expert_index, experts_dim, dtype=gate_logits.dtype)
# Set all logits to -inf that are not the sampled expert
second_place_gate_logits += (1 - second_expert_mask) * -1e9
gate_logits = (use_second_place_expert * second_place_gate_logits +
(1 - use_second_place_expert) * gate_logits)
return gate_logits
def _ntlb_gating(inputs,
outer_expert_dims,
experts_dim,
expert_capacity_dim,
hparams,
train,
variable_dtype,
importance=None,
name="ntlb_gating",
num_microbatches=None,
token_embeddings=None):
"""Compute Switch gating with no-token-left behind (NTLB) behavior."""
# SELECT EXPERT
if train:
policy = hparams.moe_switch_policy_train
else:
policy = hparams.moe_switch_policy_eval
# The internals of this function run in float32.
# bfloat16 seems to reduce quality.
gate_inputs = mtf.to_float(inputs)
# Input perturbations
if train and policy == "input_jitter":
gate_inputs = mtf.layers.multiplicative_jitter(
gate_inputs, hparams.moe_switch_jitter)
if hparams.moe_word_embed_mode is not None:
gate_inputs = _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, hparams.moe_word_embed_mode)
gate_logits = mtf.layers.dense(
gate_inputs,
experts_dim,
use_bias=False,
expert_dims=outer_expert_dims,
variable_dtype=variable_dtype,
name=name)
if hparams.moe_use_second_place_expert_prob is not None and train:
gate_logits = _stochastically_use_non_top_expert(
gate_logits, experts_dim, hparams)
raw_gates = mtf.softmax(gate_logits, reduced_dim=experts_dim)
# The internals of this function run in float32.
# bfloat16 seems to reduce quality.
raw_gates = mtf.to_float(raw_gates)
# Top-k operation
k_dim = mtf.Dimension("k", hparams.moe_ntlb_top_k)
expert_gate, expert_index = mtf.top_k(
raw_gates, reduced_dim=experts_dim, k_dim=k_dim)
expert_mask = mtf.one_hot(expert_index, experts_dim)
# LOAD BALANCING LOSS
outer_batch_dim = inputs.shape[0]
batch_dim = inputs.shape[1]
group_size_dim = inputs.shape[-2]
density_1 = mtf.reduce_mean(expert_mask, reduced_dim=group_size_dim)
density_1_proxy = mtf.reduce_mean(raw_gates, reduced_dim=group_size_dim)
if importance is not None:
expert_mask *= mtf.cast(mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
expert_gate *= mtf.cast(mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
density_1_proxy *= mtf.cast(
mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
loss = (
mtf.reduce_mean(density_1_proxy * density_1) *
float(experts_dim.size * experts_dim.size))
if num_microbatches and num_microbatches > 1:
tf.logging.info("Dividing load-balance loss by num_microbatches={}".format(
num_microbatches))
loss /= num_microbatches
# Add in the z_loss for router.
if train and hparams.moe_z_loss is not None:
tf.logging.info("Using z_loss: {}".format(hparams.moe_z_loss))
z_loss = _router_z_loss(gate_logits, experts_dim, num_microbatches,
importance)
mtf.scalar_summary(name + "/z_loss", z_loss)
loss += (hparams.moe_z_loss * z_loss)
# Logging
if train:
entropy = mtf.reduce_sum(
-raw_gates * mtf.log(raw_gates + 1e-9), reduced_dim=experts_dim)
batch_entropy = mtf.reduce_mean(entropy)
mtf.scalar_summary(name + "/entropy", batch_entropy)
mask_count_experts = mtf.reduce_sum(expert_mask, output_shape=[experts_dim])
total_routed = mtf.reduce_sum(mask_count_experts)
expert_fraction = mtf.to_float(mask_count_experts / total_routed)
split_fractions = mtf.split(
expert_fraction,
split_dim=experts_dim,
num_or_size_splits=experts_dim.size)
for fraction in split_fractions:
mtf.scalar_summary("experts/" + fraction.name.replace(":", "/"),
mtf.reduce_mean(fraction))
mtf.scalar_summary("aux_loss", mtf.reduce_mean(loss))
# COMPUTE ASSIGNMENT TO EXPERT
# Iteratively route tokens (no-token-left-behind). The idea is to route as
# many tokens as possible to top-i before then trying top-(i+1).
top_k_masks = mtf.split(
expert_mask, split_dim=k_dim, num_or_size_splits=k_dim.size)
top_k_gates = mtf.split(
expert_gate, split_dim=k_dim, num_or_size_splits=k_dim.size)
top_k_indices = mtf.split(
expert_index, split_dim=k_dim, num_or_size_splits=k_dim.size)
# Tensors cumulative values over the iterative process.
combine_tensor = mtf.constant(
inputs.mesh,
value=0,
shape=[outer_batch_dim, batch_dim, experts_dim, expert_capacity_dim])
cum_tokens = mtf.constant(
inputs.mesh, value=0, shape=[outer_batch_dim, batch_dim, experts_dim])
tokens_left_to_route = mtf.constant(
inputs.mesh, value=1., shape=[outer_batch_dim, batch_dim, group_size_dim])
expert_capacity_float = float(expert_capacity_dim.size)
for (top_i_mask, top_i_gate, top_i_index) in zip(top_k_masks, top_k_gates,
top_k_indices):
top_i_mask = mtf.reshape(
top_i_mask,
new_shape=[outer_batch_dim, batch_dim, group_size_dim, experts_dim])
# Operate only on the unrouted tokens.
top_i_mask *= tokens_left_to_route
# Record cumulative number of tokens to each expert across iterations.
cumulative_tokens_in_expert = cum_tokens + mtf.cumsum(
top_i_mask, group_size_dim)
expert_overflow = mtf.to_float(
mtf.less_equal(cumulative_tokens_in_expert, expert_capacity_float))
output_i_tokens = top_i_mask * expert_overflow
# Update the cumulative tokens routed to each expert.
cum_tokens += mtf.reduce_sum(output_i_tokens, reduced_dim=group_size_dim)
tokens_left_to_route -= (
mtf.reduce_sum(output_i_tokens, reduced_dim=experts_dim))
# Combine-tensor for this iteration
output_i_tokens_flat = mtf.reduce_sum(
output_i_tokens, reduced_dim=experts_dim)
position_in_expert = cumulative_tokens_in_expert - 1
top_i_combine_tensor = (
top_i_gate * output_i_tokens_flat *
mtf.one_hot(top_i_index, experts_dim) *
mtf.one_hot(mtf.to_int32(position_in_expert), expert_capacity_dim))
combine_tensor += top_i_combine_tensor
# Match the inputs dtype.
combine_tensor = mtf.cast(combine_tensor, inputs.dtype)
loss = mtf.cast(loss, inputs.dtype)
dispatch_tensor = mtf.cast(
mtf.cast(combine_tensor, tf.bool), combine_tensor.dtype)
return dispatch_tensor, combine_tensor, loss
def _switch_max_gating(
inputs, outer_expert_dims, experts_dim, expert_capacity_dim,
hparams, train, variable_dtype, importance=None, name="switch_max_gating",
num_microbatches=None, token_embeddings=None):
"""Compute Switch gating."""
# TODO(barretzoph,liamfedus): Refactor switch_max, switch and ntlb to limit
# code resuse.
# SELECT EXPERT
if train:
policy = hparams.moe_switch_policy_train
else:
policy = hparams.moe_switch_policy_eval
# The internals of this function run in float32.
# bfloat16 seems to reduce quality.
gate_inputs = mtf.to_float(inputs)
# Input perturbations
if policy == "input_dropout":
gate_inputs = mtf.dropout(
gate_inputs, is_training=train,
keep_prob=1.0 - hparams.moe_switch_dropout)
elif train and policy == "input_jitter":
gate_inputs = mtf.layers.multiplicative_jitter(gate_inputs,
hparams.moe_switch_jitter)
if hparams.moe_word_embed_mode is not None:
gate_inputs = _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, hparams.moe_word_embed_mode)
gate_logits = mtf.layers.dense(
gate_inputs,
experts_dim,
use_bias=False,
expert_dims=outer_expert_dims,
variable_dtype=variable_dtype,
name=name)
if hparams.moe_use_second_place_expert_prob is not None and train:
gate_logits = _stochastically_use_non_top_expert(
gate_logits, experts_dim, hparams)
raw_gates = mtf.softmax(gate_logits, reduced_dim=experts_dim)
if policy == "argmax" or policy == "input_dropout" or policy == "input_jitter":
expert_gate, expert_index = mtf.top_1(raw_gates, reduced_dim=experts_dim)
elif policy == "sample":
expert_index = mtf.sample_with_temperature(
gate_logits, experts_dim, temperature=hparams.moe_switch_temperature)
expert_gate = mtf.gather(raw_gates, expert_index, dim=experts_dim)
else:
raise ValueError("Unknown Switch gating policy %s" % policy)
expert_mask = mtf.one_hot(expert_index, experts_dim, dtype=raw_gates.dtype)
# LOAD BALANCING LOSS
group_size_dim = inputs.shape[-2]
density_1 = mtf.reduce_mean(expert_mask, reduced_dim=group_size_dim)
density_1_proxy = mtf.reduce_mean(raw_gates, reduced_dim=group_size_dim)
if importance is not None:
expert_mask *= mtf.cast(mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
expert_gate *= mtf.cast(mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
density_1_proxy *= mtf.cast(
mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
loss = (
mtf.reduce_mean(density_1_proxy * density_1) *
float(experts_dim.size * experts_dim.size))
if num_microbatches and num_microbatches > 1:
tf.logging.info("Dividing load-balance loss by num_microbatches={}".format(
num_microbatches))
loss /= num_microbatches
# Add in the z_loss for router.
if train and hparams.moe_z_loss is not None:
tf.logging.info("Using z_loss: {}".format(hparams.moe_z_loss))
z_loss = _router_z_loss(gate_logits, experts_dim, num_microbatches,
importance)
mtf.scalar_summary(name + "/z_loss", z_loss)
loss += (hparams.moe_z_loss * z_loss)
# Logging
if train:
entropy = mtf.reduce_sum(-raw_gates * mtf.log(raw_gates + 1e-9),
reduced_dim=experts_dim)
batch_entropy = mtf.reduce_mean(entropy)
mtf.scalar_summary(name + "/entropy", batch_entropy)
mtf.scalar_summary("expert_gate", mtf.reduce_mean(expert_gate))
mask_count_experts = mtf.reduce_sum(expert_mask, output_shape=[experts_dim])
total_routed = mtf.reduce_sum(mask_count_experts)
expert_fraction = mtf.to_float(mask_count_experts / total_routed)
split_fractions = mtf.split(
expert_fraction,
split_dim=experts_dim,
num_or_size_splits=experts_dim.size)
for fraction in split_fractions:
mtf.scalar_summary("experts/" + fraction.name.replace(":", "/"),
mtf.reduce_mean(fraction))
mtf.scalar_summary("aux_loss", mtf.reduce_mean(loss))
# Instead of doing the normal cumulative sum we want to take the top
# `expert_capacity` tokens. If there are less than `expert_capacity_dim`
# tokens getting routed to an expert then the combine_tensor will zero these
# out
# expert_mask shape: [outer_batch, batch, group_size, experts_unsplit]
# expert_gate shape: [outer_batch, batch, group_size]
expert_masked_probs = expert_mask * expert_gate
expert_gate_probs, expert_gate_indices = mtf.top_k(
expert_masked_probs, reduced_dim=group_size_dim,
k_dim=expert_capacity_dim)
dispatch_tensor = mtf.one_hot(
expert_gate_indices, group_size_dim, dtype=raw_gates.dtype)
combine_tensor = dispatch_tensor * expert_gate_probs
if train:
total_routed = mtf.reduce_sum(mtf.cast(mtf.greater(combine_tensor, 0.0),
dtype=raw_gates.dtype))
importance = mtf.cast(importance, dtype=total_routed.dtype)
mtf.scalar_summary("fraction_routed",
total_routed / mtf.reduce_sum(importance))
# Match the inputs dtype.
combine_tensor = mtf.cast(combine_tensor, inputs.dtype)
loss = mtf.cast(loss, inputs.dtype)
dispatch_tensor = mtf.cast(
mtf.cast(combine_tensor, tf.bool), combine_tensor.dtype)
return dispatch_tensor, combine_tensor, loss
def _expert_selection_gating(
inputs, outer_expert_dims, experts_dim, group_size_dim,
expert_capacity_dim, hparams, train, variable_dtype, importance=None,
name="expert_selection_gating", num_microbatches=None,
normalize_by_num_experts_routed=True, token_embeddings=None):
"""Compute gating where each expert chooses what tokens it wants."""
# Select the randomization policy.
if train:
policy = hparams.moe_switch_policy_train
else:
policy = hparams.moe_switch_policy_eval
# The internals of this function run in float32 otherwise instabilities
# can occur.
gate_inputs = mtf.to_float(inputs)
# Input perturbations for exploration.
if policy == "input_dropout":
gate_inputs = mtf.dropout(gate_inputs, is_training=train,
keep_prob=1.0 - hparams.moe_switch_dropout)
elif train and policy == "input_jitter":
gate_inputs = mtf.layers.multiplicative_jitter(gate_inputs,
hparams.moe_switch_jitter)
if hparams.moe_word_embed_mode is not None:
gate_inputs = _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, hparams.moe_word_embed_mode)
# Compute expert logits for each token.
# gate_logits shape: [outer_batch, batch, group, expert_unsplit]
gate_logits = mtf.layers.dense(
gate_inputs,
experts_dim,
use_bias=False,
expert_dims=outer_expert_dims,
variable_dtype=variable_dtype,
name=name)
# Set tokens to -inf before softmax if importance is zero as softmax is
# normalized over all tokens in the group.
if importance is not None:
gate_logits += mtf.cast(
mtf.equal(importance, 0.0), dtype=gate_logits.dtype) * -1e9
raw_gates = mtf.softmax(gate_logits, reduced_dim=group_size_dim)
# expert_gate_probs shape:
# [outer_batch, batch, expert_unsplit, expert_capacity]
# expert_gate_indices shape:
# [outer_batch, batch, expert_unsplit, expert_capacity]
expert_gate_probs, expert_gate_indices = mtf.top_k(
raw_gates, reduced_dim=group_size_dim, k_dim=expert_capacity_dim)
# dispatch_tensor shape:
# [outer_batch, batch, expert_unsplit, expert_capacity, group]
dispatch_tensor = mtf.one_hot(
expert_gate_indices, group_size_dim, dtype=raw_gates.dtype)
# combine_tensor shape:
# [outer_batch, batch, expert_unsplit, expert_capacity, group]
combine_tensor = dispatch_tensor * expert_gate_probs
# Tokens will be aggregated across many experts and will not
# be normalized. This could be an issue, so might want to normalize by the
# number of experts each token is sent to.
if normalize_by_num_experts_routed:
num_experts_routed = mtf.reduce_sum(
dispatch_tensor,
output_shape=(dispatch_tensor.shape[:2] + [group_size_dim]))
combine_tensor /= mtf.maximum(num_experts_routed, 1.0)
################### Compute the load balancing loss ###################
# Push `aggregated_group_probs` of size `group` (which sums to num_experts)
# to be uniform.
# aggregated_group_probs shape: [outer_batch, batch, group]
# importance shape: [outer_batch, batch, group]
aggregated_group_probs = mtf.reduce_mean(raw_gates, reduced_dim=experts_dim)
if importance is not None:
aggregated_group_probs *= mtf.cast(
mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
# Scale loss by group_size to keep loss constant across different group_sizes.
# true_group_size is number of tokens per group that are not masked out.
true_group_size = mtf.cast(
mtf.reduce_sum(importance, reduced_dim=group_size_dim),
dtype=raw_gates.dtype)
loss = (mtf.reduce_mean(
aggregated_group_probs * aggregated_group_probs * true_group_size) *
float(group_size_dim.size))
if num_microbatches and num_microbatches > 1:
tf.logging.info("Dividing load-balance loss by num_microbatches={}".format(
num_microbatches))
loss /= num_microbatches
# Add in the z_loss for router.
if train and hparams.moe_z_loss is not None:
tf.logging.info("Using z_loss: {}".format(hparams.moe_z_loss))
z_loss = _router_z_loss(gate_logits, experts_dim, num_microbatches,
importance)
mtf.scalar_summary(name + "/z_loss", z_loss)
loss += (hparams.moe_z_loss * z_loss)
################### Logging ###################
if train:
entropy = mtf.reduce_sum(-raw_gates * mtf.log(raw_gates + 1e-9),
reduced_dim=group_size_dim)
batch_entropy = mtf.reduce_mean(entropy)
mtf.scalar_summary(name + "/entropy", batch_entropy)
# Log for each token in the group how many experts it gets sent to.
num_experts_sent_per_token = (
mtf.reduce_sum(dispatch_tensor, output_shape=[group_size_dim]) *
float(experts_dim.size * expert_capacity_dim.size))
split_fractions = mtf.split(
num_experts_sent_per_token,
split_dim=group_size_dim,
num_or_size_splits=group_size_dim.size)
for fraction in split_fractions:
mtf.scalar_summary("group_token/" + fraction.name.replace(":", "/"),
mtf.reduce_sum(fraction))
mtf.scalar_summary("aux_loss", mtf.reduce_mean(loss))
#################### Match the inputs dtype ###################
combine_tensor = mtf.cast(combine_tensor, inputs.dtype)
loss = mtf.cast(loss, inputs.dtype)
dispatch_tensor = mtf.cast(
mtf.cast(dispatch_tensor, tf.bool), combine_tensor.dtype)
return dispatch_tensor, combine_tensor, loss
def _switch_gating(
inputs, outer_expert_dims, experts_dim, expert_capacity_dim,
hparams, train, variable_dtype, importance=None, name="switch_gating",
num_microbatches=None, token_embeddings=None):
"""Compute Switch gating."""
# SELECT EXPERT
if train:
policy = hparams.moe_switch_policy_train
else:
policy = hparams.moe_switch_policy_eval
# The internals of this function run in float32.
# bfloat16 seems to reduce quality.
gate_inputs = mtf.to_float(inputs)
# Input perturbations
if policy == "input_dropout":
gate_inputs = mtf.dropout(
gate_inputs,
is_training=train,
keep_prob=1.0 - hparams.moe_switch_dropout)
elif train and policy == "input_jitter":
gate_inputs = mtf.layers.multiplicative_jitter(gate_inputs,
hparams.moe_switch_jitter)
if hparams.moe_word_embed_mode is not None:
gate_inputs = _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, hparams.moe_word_embed_mode)
gate_logits = mtf.layers.dense(
gate_inputs,
experts_dim,
use_bias=False,
expert_dims=outer_expert_dims,
variable_dtype=variable_dtype,
name=name)
if hparams.moe_use_second_place_expert_prob is not None and train:
gate_logits = _stochastically_use_non_top_expert(
gate_logits, experts_dim, hparams)
raw_gates = mtf.softmax(gate_logits, reduced_dim=experts_dim)
if policy == "argmax" or policy == "input_dropout" or policy == "input_jitter":
expert_gate, expert_index = mtf.top_1(raw_gates, reduced_dim=experts_dim)
elif policy == "sample":
expert_index = mtf.sample_with_temperature(
gate_logits, experts_dim, temperature=hparams.moe_switch_temperature)
expert_gate = mtf.gather(raw_gates, expert_index, dim=experts_dim)
else:
raise ValueError("Unknown Switch gating policy %s" % policy)
expert_mask = mtf.one_hot(expert_index, experts_dim, dtype=raw_gates.dtype)
# LOAD BALANCING LOSS
group_size_dim = inputs.shape[-2]
density_1 = mtf.reduce_mean(expert_mask, reduced_dim=group_size_dim)
density_1_proxy = mtf.reduce_mean(raw_gates, reduced_dim=group_size_dim)
if importance is not None:
expert_mask *= mtf.cast(mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
expert_gate *= mtf.cast(mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
density_1_proxy *= mtf.cast(
mtf.equal(importance, 1.0), dtype=raw_gates.dtype)
loss = (
mtf.reduce_mean(density_1_proxy * density_1) *
float(experts_dim.size * experts_dim.size))
if num_microbatches and num_microbatches > 1:
tf.logging.info("Dividing load-balance loss by num_microbatches={}".format(
num_microbatches))
loss /= num_microbatches
# Logging
if train:
entropy = mtf.reduce_sum(-raw_gates * mtf.log(raw_gates + 1e-9),
reduced_dim=experts_dim)
batch_entropy = mtf.reduce_mean(entropy)
mtf.scalar_summary(name + "/entropy", batch_entropy)
mtf.scalar_summary("expert_gate", mtf.reduce_mean(expert_gate))
mask_count_experts = mtf.reduce_sum(expert_mask, output_shape=[experts_dim])
total_routed = mtf.reduce_sum(mask_count_experts)
expert_fraction = mtf.to_float(mask_count_experts / total_routed)
split_fractions = mtf.split(
expert_fraction,
split_dim=experts_dim,
num_or_size_splits=experts_dim.size)
for fraction in split_fractions:
mtf.scalar_summary("experts/" + fraction.name.replace(":", "/"),
mtf.reduce_mean(fraction))
mtf.scalar_summary("aux_loss", mtf.reduce_mean(loss))
# Add in the z_loss for router.
if train and hparams.moe_z_loss is not None:
tf.logging.info("Using z_loss: {}".format(hparams.moe_z_loss))
z_loss = _router_z_loss(gate_logits, experts_dim, num_microbatches,
importance)
mtf.scalar_summary(name + "/z_loss", z_loss)
loss += (hparams.moe_z_loss * z_loss)
# COMPUTE ASSIGNMENT TO EXPERT
# Experts have a limited capacity, ensure we do not exceed it. Construct
# the batch indices, to each expert, with position_in_expert
position_in_expert = mtf.cumsum(
expert_mask, group_size_dim, exclusive=True) * expert_mask
position_in_expert = mtf.cast(position_in_expert, dtype=raw_gates.dtype)
# Keep only tokens that fit within expert_capacity.
expert_capacity_float = float(expert_capacity_dim.size)
expert_mask *= mtf.cast(
mtf.less(position_in_expert, expert_capacity_float),
dtype=raw_gates.dtype)
expert_mask_flat = mtf.reduce_sum(expert_mask, reduced_dim=experts_dim)
if train:
total_routed = mtf.reduce_sum(expert_mask_flat)
importance = mtf.cast(importance, dtype=total_routed.dtype)
mtf.scalar_summary("fraction_routed",
total_routed / mtf.reduce_sum(importance))
# Mask out the experts that have overflowed expert capacity. Sparsify the
# expert_gate.
expert_gate *= expert_mask_flat
combine_tensor = (
expert_gate * expert_mask_flat *
mtf.one_hot(expert_index, experts_dim, dtype=raw_gates.dtype) *
mtf.one_hot(
mtf.to_int32(position_in_expert),
expert_capacity_dim,
dtype=raw_gates.dtype))
# Match the inputs dtype.
combine_tensor = mtf.cast(combine_tensor, inputs.dtype)
loss = mtf.cast(loss, inputs.dtype)
dispatch_tensor = mtf.cast(
mtf.cast(combine_tensor, tf.bool), combine_tensor.dtype)
return dispatch_tensor, combine_tensor, loss
def _top_2_gating(
inputs, outer_expert_dims, experts_dim, expert_capacity_dim,
hparams, train, variable_dtype, importance=None, name="top_2_gating",
num_microbatches=None, token_embeddings=None):
"""Compute gating for mixture-of-experts in TensorFlow.
Note: until the algorithm and inferface solidify, we pass in a hyperparameters
dictionary in order not to complicate the interface in mtf_transformer.py .
Once this code moves out of "research", we should pass the hyperparameters
separately.
Hyperparameters used:
hparams.moe_use_second_place_loss: a boolean
hparams.moe_second_policy_train: a string
hparams.moe_second_policy_eval: a string
hparams.moe_second_threshold: a float
The returned forward assignment is a tensor used to map (via einsum) from the
inputs to the expert_inputs. Likewise, the returned combine_tensor is
used to map (via einsum) from the expert outputs to the outputs. Both the
forward and backward assignments are mostly zeros. The shapes of the tensors
are as follows.
inputs: [<batch_dims>, group_size_dim, input_dim]
importance: [<batch_dims>, group_size_dim]
dispatch_tensor:
[<batch_dims>, group_size_dim, experts_dim, expert_capacity_dim]
expert_inputs:
[<batch_dims>, experts_dim, expert_capacity_dim, input_dim]
expert_outputs: [<batch_dims>, experts_dim, expert_capacity_dim, output_dim]
combine_tensor:
[<batch_dims>, group_size_dim, experts_dim, expert_capacity_dim]
outputs: [<batch_dims>, group_size_dim, output_dim]
"importance" is an optional tensor with one floating-point value for each
input vector. If the importance of an input is 1.0, then we send it to
up to 2 experts. If 0.0 < importance < 1.0, then we send it to at most
one expert. If importance == 0.0, then we send it to no experts.
We use "importance" at the second-level gating function of a hierarchical
mixture of experts. Inputs to the first-choice expert-group get importance
1.0. Inputs to the second-choice expert group get importance 0.5.
Inputs that represent padding get importance 0.0.
Args:
inputs: a mtf.Tensor with shape [<batch_dims>, group_size_dim, input_dim]
outer_expert_dims: an optional list of dimensions. This is for the case
where we are at an inner level of a hierarchical MoE.
experts_dim: a Dimension (the number of experts)
expert_capacity_dim: a Dimension (number of examples per group per expert)
hparams: model hyperparameters.
train: a boolean
variable_dtype: a mtf.VariableDType
importance: an optional tensor with shape [<batch_dims>, group_size_dim]
name: an optional string
num_microbatches: number of microbatches.
token_embeddings: an optional tensor with shape
[<batch_dims>, group_size_dim, input_dim] that is the input
word embeddings.
Returns:
dispatch_tensor: a Tensor with shape
[<batch_dims>, group_size_dim, experts_dim, expert_capacity_dim]
combine_tensor: a Tensor with shape
[<batch_dims>, group_size_dim, experts_dim, expert_capacity_dim]
loss: a mtf scalar
Raises:
ValueError: on illegal hyperparameters
"""
group_size_dim, unused_input_dim = inputs.shape.dims[-2:]
# The internals of this function run in float32.
# bfloat16 seems to reduce quality.
gate_inputs = mtf.to_float(inputs)
if hparams.moe_word_embed_mode is not None:
gate_inputs = _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, hparams.moe_word_embed_mode)
gate_logits = mtf.layers.dense(
gate_inputs, experts_dim, use_bias=False,
expert_dims=outer_expert_dims,
variable_dtype=variable_dtype,
name=name)
raw_gates = mtf.softmax(gate_logits, experts_dim)
expert_capacity_f = float(expert_capacity_dim.size)
# FIND TOP 2 EXPERTS PER POSITON
# Find the top expert for each position. shape=[batch, group]
gate_1, index_1 = mtf.top_1(raw_gates, experts_dim)
# [batch, group, experts]
mask_1 = mtf.one_hot(index_1, experts_dim, dtype=raw_gates.dtype)
density_1_proxy = raw_gates
if importance is not None:
mask_1 *= mtf.to_float(mtf.equal(importance, 1.0))
gate_1 *= mtf.to_float(mtf.equal(importance, 1.0))
density_1_proxy *= mtf.to_float(mtf.equal(importance, 1.0))
gates_without_top_1 = raw_gates * (1.0 - mask_1)
# [batch, group]
gate_2, index_2 = mtf.top_1(gates_without_top_1, experts_dim)
# [batch, group, experts]
mask_2 = mtf.one_hot(index_2, experts_dim, dtype=raw_gates.dtype)
if importance is not None:
mask_2 *= mtf.to_float(mtf.greater(importance, 0.0))
denom = gate_1 + gate_2 + 1e-9
gate_1 /= denom
gate_2 /= denom
# BALANCING LOSSES
# shape = [batch, experts]
# We want to equalize the fraction of the batch assigned to each expert
density_1 = mtf.reduce_mean(mask_1, reduced_dim=group_size_dim)
# Something continuous that is correlated with what we want to equalize.
density_1_proxy = mtf.reduce_mean(density_1_proxy, reduced_dim=group_size_dim)
loss = (mtf.reduce_mean(density_1_proxy * density_1)
* float(experts_dim.size * experts_dim.size))
if hparams.moe_use_second_place_loss:
# Also add a loss to encourage all experts to be used equally also as the
# second-place expert. Experimentally, this seems to be a wash.
# We want to equalize the fraction of the batch assigned to each expert:
density_2 = mtf.reduce_mean(mask_2, reduced_dim=group_size_dim)
# As a proxy for density_2, we renormalize the raw gates after the top one
# has been removed.
normalized = gates_without_top_1 / (
mtf.reduce_sum(gates_without_top_1, reduced_dim=experts_dim) + 1e-9)
density_2_proxy = mtf.reduce_mean(normalized, reduced_dim=group_size_dim)
loss_2 = (mtf.reduce_mean(density_2_proxy * density_2)
* float(experts_dim.size * experts_dim.size))
loss += loss_2 * 0.5
if num_microbatches and num_microbatches > 1:
tf.logging.info("Dividing load-balance loss by num_microbatches={}".format(
num_microbatches))
loss /= num_microbatches
# Add in the z_loss for router.
if train and hparams.moe_z_loss is not None:
tf.logging.info("Using z_loss: {}".format(hparams.moe_z_loss))
z_loss = _router_z_loss(gate_logits, experts_dim, num_microbatches,
importance)
mtf.scalar_summary(name + "/z_loss", z_loss)
loss += (hparams.moe_z_loss * z_loss)
# Depending on the policy in the hparams, we may drop out some of the
# second-place experts.
if train:
policy = hparams.moe_second_policy_train
threshold = hparams.moe_second_threshold_train
else:
policy = hparams.moe_second_policy_eval
threshold = hparams.moe_second_threshold_eval
if policy == "all":
# Use second-place experts for all examples.
pass
elif policy == "none":
# Never use second-place experts for all examples.
mask_2 = mtf.zeros_like(mask_2)
elif policy == "threshold":
# Use second-place experts if gate_2 > threshold.
mask_2 *= mtf.to_float(mtf.greater(gate_2, threshold))
elif policy == "random":
# Use second-place experts with probablity min(1.0, gate_2 / threshold).
mask_2 *= mtf.to_float(
mtf.less(mtf.random_uniform(gate_2.mesh, gate_2.shape),
gate_2 / max(threshold, 1e-9)))
else:
raise ValueError("Unknown policy %s" % policy)
# COMPUTE ASSIGNMENT TO EXPERTS
# [batch, group, experts]
# This is the position within the expert's mini-batch for this sequence
position_in_expert_1 = mtf.cumsum(
mask_1, group_size_dim, exclusive=True) * mask_1
# Remove the elements that don't fit. [batch, group, experts]
mask_1 *= mtf.to_float(mtf.less(position_in_expert_1, expert_capacity_f))
# [batch, experts]
# How many examples in this sequence go to this expert
mask_1_count = mtf.reduce_sum(mask_1, reduced_dim=group_size_dim)
# [batch, group] - mostly ones, but zeros where something didn't fit
mask_1_flat = mtf.reduce_sum(mask_1, reduced_dim=experts_dim)
# [batch, group]
position_in_expert_1 = mtf.reduce_sum(
position_in_expert_1, reduced_dim=experts_dim)
# Weight assigned to first expert. [batch, group]
gate_1 *= mask_1_flat
# [batch, group, experts]
position_in_expert_2 = (
mtf.cumsum(mask_2, group_size_dim, exclusive=True) + mask_1_count)
position_in_expert_2 *= mask_2
mask_2 *= mtf.to_float(mtf.less(position_in_expert_2, expert_capacity_f))
# mask_2_count = mtf.reduce_sum(mask_2, reduced_dim=experts_dim)
mask_2_flat = mtf.reduce_sum(mask_2, reduced_dim=experts_dim)
gate_2 *= mask_2_flat
position_in_expert_2 = mtf.reduce_sum(
position_in_expert_2, reduced_dim=experts_dim)
if train:
# Gate entropy.
if importance is not None:
raw_gates *= mtf.to_float(mtf.greater(importance, 0.0))
entropy = mtf.reduce_sum(-raw_gates * mtf.log(raw_gates + 1e-9),
reduced_dim=experts_dim)
batch_entropy = mtf.reduce_mean(entropy)
mtf.scalar_summary(name + "/entropy", batch_entropy)
# Mean top-1 and top-2 normalized gate probabilities.
if importance is not None:
gate_2 *= mtf.to_float(mtf.greater(importance, 0.0))
mtf.scalar_summary("top1_gate_normalized", mtf.reduce_mean(gate_1))
mtf.scalar_summary("top2_gate_normalized", mtf.reduce_mean(gate_2))
top1_routed = mtf.reduce_sum(mask_1_flat)
top2_routed = mtf.reduce_sum(mask_2_flat)
importance = mtf.cast(importance, dtype=top1_routed.dtype)
# What fraction of the top-1 and top-2 tokens are being routed to any
# expert.
mtf.scalar_summary("top1_fraction_routed",
top1_routed / mtf.reduce_sum(importance))
mtf.scalar_summary("top2_fraction_routed",
top2_routed / mtf.reduce_sum(importance))
# One or zero if that token got routed anywhere.
total_routed = mtf.reduce_sum(mtf.minimum(
mask_1_flat + mask_2_flat, mtf.ones_like(top1_routed)))
mtf.scalar_summary("all_fraction_routed",
total_routed / mtf.reduce_sum(importance))
mtf.scalar_summary("aux_loss", mtf.reduce_mean(loss))
# Log what fraction of tokens are going to each expert.
def _log_per_expert_fraction(mask, name):
# mask: [batch, group, experts]
tokens_per_expert = mtf.reduce_sum(mask, output_shape=[experts_dim])
total_routed = mtf.reduce_sum(tokens_per_expert)
expert_fraction = mtf.to_float(tokens_per_expert / total_routed)
split_fractions = mtf.split(
expert_fraction,
split_dim=experts_dim,
num_or_size_splits=experts_dim.size)
for fraction in split_fractions:
mtf.scalar_summary(name + "_experts/" + fraction.name.replace(":", "/"),
mtf.reduce_mean(fraction))
_log_per_expert_fraction(mask_1, "top1")
_log_per_expert_fraction(mask_2, "top2")
_log_per_expert_fraction(mask_1 + mask_2, "all")
# [batch, group, experts, expert_capacity]
combine_tensor = (
gate_1 * mask_1_flat
* mtf.one_hot(index_1, experts_dim)
* mtf.one_hot(mtf.to_int32(position_in_expert_1), expert_capacity_dim) +
gate_2 * mask_2_flat
* mtf.one_hot(index_2, experts_dim)
* mtf.one_hot(mtf.to_int32(position_in_expert_2), expert_capacity_dim))
combine_tensor = mtf.cast(combine_tensor, inputs.dtype)
loss = mtf.cast(loss, inputs.dtype)
dispatch_tensor = mtf.cast(
mtf.cast(combine_tensor, tf.bool), combine_tensor.dtype)
return dispatch_tensor, combine_tensor, loss
def _top_n_gating(
inputs, outer_expert_dims, experts_dim, expert_capacity_dim,
hparams, train, variable_dtype, importance=None, name="top_n_gating",
num_microbatches=None, token_embeddings=None):
"""Compute generalization of top-2 gating for mixture-of-experts.
Hyperparameters used:
hparams.moe_use_second_place_loss: a boolean
hparams.moe_second_policy_train: a string
hparams.moe_second_policy_eval: a string
hparams.moe_second_threshold: a float
hparams.moe_top_n_num_experts_per_token: an int
Tensor shapes are largely the same as in top_2 gating, so see that docstring
for more details.
Args:
inputs: a mtf.Tensor with shape [<batch_dims>, group_size_dim, input_dim]
outer_expert_dims: an optional list of dimensions. This is for the case
where we are at an inner level of a hierarchical MoE.
experts_dim: a Dimension (the number of experts)
expert_capacity_dim: a Dimension (number of examples per group per expert)
hparams: model hyperparameters.
train: a boolean
variable_dtype: a mtf.VariableDType
importance: an optional tensor with shape [<batch_dims>, group_size_dim]
name: an optional string
num_microbatches: number of microbatches.
token_embeddings: an optional tensor with shape
[<batch_dims>, group_size_dim, input_dim] that is the input
word embeddings.
Returns:
dispatch_tensor: a Tensor with shape
[<batch_dims>, group_size_dim, experts_dim, expert_capacity_dim]
combine_tensor: a Tensor with shape
[<batch_dims>, group_size_dim, experts_dim, expert_capacity_dim]
loss: a mtf scalar
Raises:
ValueError: on illegal hyperparameters
"""
group_size_dim, unused_input_dim = inputs.shape.dims[-2:]
# The internals of this function run in float32.
# bfloat16 seems to reduce quality.
gate_inputs = mtf.to_float(inputs)
if hparams.moe_word_embed_mode is not None:
gate_inputs = _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, hparams.moe_word_embed_mode)
gate_logits = mtf.layers.dense(
gate_inputs, experts_dim, use_bias=False,
expert_dims=outer_expert_dims,
variable_dtype=variable_dtype,
name=name)
raw_gates = mtf.softmax(gate_logits, experts_dim)
expert_capacity_f = float(expert_capacity_dim.size)
# Used for aux loss.
density_1_proxy = raw_gates
if importance is not None:
density_1_proxy *= mtf.to_float(mtf.equal(importance, 1.0))
# Loop over the get the top-n tokens and their masks.
gates = []
masks = []
indexes = []
# Tensor that contains all but the top-n highest experts for each token.
gates_without_top_n = raw_gates
gates_without_top_1 = None # Used for second place loss
for n in range(hparams.moe_top_n_num_experts_per_token):
# [batch, group]
gate_n, index_n = mtf.top_1(gates_without_top_n, experts_dim)
# [batch, group, experts]
mask_n = mtf.one_hot(index_n, experts_dim, dtype=raw_gates.dtype)
if importance is not None:
mask_n *= mtf.to_float(mtf.greater(importance, 0.0))
gate_n *= mtf.to_float(mtf.greater(importance, 0.0))
gates_without_top_n *= (1.0 - mask_n)
# Used for second place loss.
if n == 1:
gates_without_top_1 = gates_without_top_n
gates.append(gate_n)
masks.append(mask_n)
indexes.append(index_n)
if len(gates) > 1:
# All gates probs are normalized over the top-n tokens.
denom = mtf.add_n(gates) + 1e-9
gates = [gate / denom for gate in gates]
# BALANCING LOSSES
# shape = [batch, experts]
# We want to equalize the fraction of the batch assigned to each expert.
mask_1 = masks[0] # Mask for top-1 token.
density_1 = mtf.reduce_mean(mask_1, reduced_dim=group_size_dim)
# Something continuous that is correlated with what we want to equalize.
density_1_proxy = mtf.reduce_mean(density_1_proxy, reduced_dim=group_size_dim)
loss = (mtf.reduce_mean(density_1_proxy * density_1)
* float(experts_dim.size * experts_dim.size))
# TODO(barretzoph): Add in options for aux losses for n > 2.
if hparams.moe_use_second_place_loss:
pass
# Also add a loss to encourage all experts to be used equally also as the
# second-place expert. Experimentally, this seems to be a wash.
# We want to equalize the fraction of the batch assigned to each expert:
density_2 = mtf.reduce_mean(masks[2], reduced_dim=group_size_dim)
# As a proxy for density_2, we renormalize the raw gates after the top one
# has been removed.
normalized = gates_without_top_1 / (
mtf.reduce_sum(gates_without_top_1, reduced_dim=experts_dim) + 1e-9)
density_2_proxy = mtf.reduce_mean(normalized, reduced_dim=group_size_dim)
loss_2 = (mtf.reduce_mean(density_2_proxy * density_2)
* float(experts_dim.size * experts_dim.size))
loss += loss_2 * 0.5
if num_microbatches and num_microbatches > 1:
tf.logging.info("Dividing load-balance loss by num_microbatches={}".format(
num_microbatches))
loss /= num_microbatches
# Add in the z_loss for router.
if train and hparams.moe_z_loss is not None:
tf.logging.info("Using z_loss: {}".format(hparams.moe_z_loss))
z_loss = _router_z_loss(gate_logits, experts_dim, num_microbatches,
importance)
mtf.scalar_summary(name + "/z_loss", z_loss)
loss += (hparams.moe_z_loss * z_loss)
# Depending on the policy in the hparams, we may drop out some of the
# second-place experts.
def _update_mask_based_on_gate_value(gate_n, mask_n):
"""Update the mask based in the policy and the threshold for n>1.
Args:
gate_n: normalized router probability for the nth highest expert.
mask_n: boolean one-hot tensor that keeps track of the nth expert to
send to each toke. This also masks away tokens that will not be routed.
Returns:
An altered mask_n that will mask out any top-n token that doesn't follow
the second_policy method and threshold.
"""
if train:
policy = hparams.moe_second_policy_train
threshold = hparams.moe_second_threshold_train
else:
policy = hparams.moe_second_policy_eval
threshold = hparams.moe_second_threshold_eval
if policy == "all":
# Use nth-place experts for all examples.
pass
elif policy == "none":
# Never use nth-place experts for all examples.
mask_n = mtf.zeros_like(mask_n)
elif policy == "threshold":
# Use nth-place experts if gate_n > threshold.
mask_n *= mtf.to_float(mtf.greater(gate_n, threshold))
elif policy == "random":
# Use nth-place experts with probablity min(1.0, gate_n / threshold).
mask_n *= mtf.to_float(
mtf.less(mtf.random_uniform(gate_n.mesh, gate_n.shape),
gate_n / max(threshold, 1e-9)))
else:
raise ValueError("Unknown policy %s" % policy)
return mask_n
# Now update masks for n>1 to reflect how these additional tokens should be
# routed according to their corresponding policies.
# Only update for n>1 as we always want to route the top-1 token.
for i in range(1, len(masks)):
masks[i] = _update_mask_based_on_gate_value(gates[i], masks[i])
def _compute_top_n_mask(gate_n, mask_n, index_n, prev_mask_count):
# This is the position within the expert's mini-batch for this sequence.
position_in_expert_n = (
mtf.cumsum(mask_n, group_size_dim, exclusive=True) + prev_mask_count)
# Mask out tokens that should not be routed.
position_in_expert_n *= mask_n
# Remove the elements that don't fit. [batch, group, experts]
mask_n *= mtf.to_float(mtf.less(position_in_expert_n, expert_capacity_f))
# [batch, experts]
# How many examples in this sequence go to this expert.
mask_n_count = mtf.reduce_sum(mask_n, reduced_dim=group_size_dim)
# Keep running sum of total tokens sent to each expert.
prev_mask_count += mask_n_count
# [batch, group] - mostly ones, but zeros where something didn't fit.
mask_n_flat = mtf.reduce_sum(mask_n, reduced_dim=experts_dim)
# Weight assigned to nth expert. [batch, group]
gate_n *= mask_n_flat
# [batch, group]
position_in_expert_n = mtf.reduce_sum(
position_in_expert_n, reduced_dim=experts_dim)
partial_combine_tensor = (
gate_n * mask_n_flat
* mtf.one_hot(index_n, experts_dim)
* mtf.one_hot(mtf.to_int32(position_in_expert_n), expert_capacity_dim))
return prev_mask_count, partial_combine_tensor
# [batch, experts]
# How many examples in this group go to each expert. This starts at zero.
prev_mask_count = 0.0
partial_combine_tensors = []
for gate_n, mask_n, index_n in zip(gates, masks, indexes):
prev_mask_count, partial_combine_tensor = _compute_top_n_mask(
gate_n, mask_n, index_n, prev_mask_count)
partial_combine_tensors.append(partial_combine_tensor)
combine_tensor = mtf.add_n(partial_combine_tensors)
combine_tensor = mtf.cast(combine_tensor, inputs.dtype)
loss = mtf.cast(loss, inputs.dtype)
dispatch_tensor = mtf.cast(
mtf.cast(combine_tensor, tf.bool), combine_tensor.dtype)
return dispatch_tensor, combine_tensor, loss
def _add_token_emb_to_gate_inputs(
gate_inputs, token_embeddings, moe_word_embed_mode):
"""Add token_embeddings to gate_inputs based on moe_word_embed_mode."""
token_embeddings = mtf.to_float(token_embeddings)
if moe_word_embed_mode == "concat":
gate_inputs = mtf.concat(
[gate_inputs, token_embeddings], gate_inputs.shape.dims[-1].name)
elif moe_word_embed_mode == "concat_stop_grad":
token_embeddings = mtf.stop_gradient(token_embeddings)
gate_inputs = mtf.concat(
[gate_inputs, token_embeddings], gate_inputs.shape.dims[-1].name)
elif moe_word_embed_mode == "add":
gate_inputs += token_embeddings
elif moe_word_embed_mode == "add_stop_grad":
gate_inputs += mtf.stop_gradient(token_embeddings)
elif moe_word_embed_mode == "embed_only":
gate_inputs = token_embeddings
else:
raise ValueError("Unimplemented moe word embed mode: {}".format(
moe_word_embed_mode))
return gate_inputs
def _router_z_loss(logits, experts_dim, num_microbatches, importance=None):
"""Loss that encourages router logits to remain small and improves stability.
Args:
logits: a tensor with shape [<batch_dims>, experts_dim]
experts_dim: a Dimension (the number of experts)
num_microbatches: number of microbatches
importance: an optional tensor with shape [<batch_dims>, group_size_dim]
Returns:
z_loss: scalar loss only applied by non-padded tokens and normalized by
num_microbatches.
"""
log_z = mtf.reduce_logsumexp(logits, experts_dim)
z_loss = mtf.square(log_z)
if importance is not None:
z_loss *= mtf.cast(mtf.equal(importance, 1.0), dtype=z_loss.dtype)
denom = mtf.reduce_sum(
mtf.cast(mtf.equal(importance, 1.0), dtype=z_loss.dtype))
z_loss = mtf.reduce_sum(z_loss) / (denom * num_microbatches)
return z_loss
def set_default_moe_hparams(hparams):
"""Add necessary hyperparameters for mixture-of-experts."""
hparams.moe_num_experts = 16
hparams.moe_loss_coef = 1e-2
hparams.add_hparam("moe_gating", "top_2")
# Experts have fixed capacity per batch. We need some extra capacity
# in case gating is not perfectly balanced.
# moe_capacity_factor_* should be set to a value >=1.
hparams.add_hparam("moe_capacity_factor_train", 1.25)
hparams.add_hparam("moe_capacity_factor_eval", 2.0)
hparams.add_hparam("moe_capacity_factor_second_level", 1.0)
# Each expert has a hidden layer with this size.
hparams.add_hparam("moe_hidden_size", 4096)
# For gating, divide inputs into groups of this size before gating.
# Each group sends the same number of inputs to each expert.
# Ideally, the group size would be the whole batch, but this is expensive
# due to our use of matrix multiplication for reordering.
hparams.add_hparam("moe_group_size", 1024)
# For top_2 gating, whether to impose an additional loss in order to make
# the experts equally used as the second-place expert.
hparams.add_hparam("moe_use_second_place_loss", 0)
# In top_2 gating, policy for whether to use a second-place expert.
# Legal values are:
# "all": always
# "none": never
# "threshold": if gate value > the given threshold
# "random": if gate value > threshold*random_uniform(0,1)
hparams.add_hparam("moe_second_policy_train", "random")
hparams.add_hparam("moe_second_policy_eval", "random")
hparams.add_hparam("moe_second_threshold_train", 0.2)
hparams.add_hparam("moe_second_threshold_eval", 0.2)
def _split_into_groups(n, max_group_size, mesh_dim_size):
"""Helper function for figuring out how to split a dimension into groups.
We have a dimension with size n and we want to split it into
two dimensions: n = num_groups * group_size
group_size should be the largest possible value meeting the constraints:
group_size <= max_group_size
(num_groups = n/group_size) is a multiple of mesh_dim_size
Args:
n: an integer
max_group_size: an integer
mesh_dim_size: an integer
Returns:
num_groups: an integer
group_size: an integer
Raises:
ValueError: if n is not a multiple of mesh_dim_size
"""
if n % mesh_dim_size != 0:
raise ValueError(
"n=%d is not a multiple of mesh_dim_size=%d" % (n, mesh_dim_size))
num_groups = max(1, n // max_group_size)
while (num_groups % mesh_dim_size != 0 or n % num_groups != 0):
num_groups += 1
group_size = n // num_groups
tf.logging.info(
"_split_into_groups(n=%d, max_group_size=%d, mesh_dim_size=%d)"
" = (num_groups=%d group_size=%d)" %
(n, max_group_size, mesh_dim_size, num_groups, group_size))
return num_groups, group_size
class HParams(object):
"""Replacement for tf.contrib.training.HParams.
TODO(noam): remove this class and rewrite the methods in this file.
"""
def __init__(self, **kwargs):
for k, v in kwargs.items():
setattr(self, k, v)
def add_hparam(self, k, v):
setattr(self, k, v)摘要
规模为自然语言处理开辟了新的前沿,但代价高昂。作为回应,专家混合模型(Mixture-of-Experts, MoE)和Switch Transformers被提出,作为通向更大、更强大语言模型的节能路径。然而,广泛的自然语言任务中的最新进展受到训练不稳定性和微调期间质量不确定性的阻碍。我们的工作聚焦于这些问题,并作为设计指南。我们最终将稀疏模型扩展到2690亿参数,计算成本与320亿参数的密集编码器-解码器Transformer相当(稳定且可迁移的专家混合模型,ST-MoE-32B)。这是首次稀疏模型在迁移学习中实现了最先进的性能,涵盖推理(SuperGLUE, ARC Easy, ARC Challenge)、摘要(XSum, CNN-DM)、闭卷问答(WebQA, Natural Questions)和对抗性构建任务(Winogrande, ANLI R3)等多种任务。
1 引言
稀疏专家神经网络展示了规模的优势,并为当今常用的静态神经网络架构提供了高效的替代方案(Raffel et al., 2019; Brown et al., 2020; Rae et al., 2021)。与对所有输入应用相同参数不同,稀疏专家网络动态选择每个输入使用的参数(Shazeer et al., 2017)。这使得网络能够大幅扩展参数数量,同时保持每个token的FLOPs大致不变。这些方法已经产生了最先进的翻译模型(Lepikhin et al., 2020),4-7倍的预训练加速(Fedus et al., 2021; Artetxe et al., 2021),以及使用1/3的能源训练成本达到GPT-3级别的一次性性能(Du et al., 2021)。尽管参数数量惊人,稀疏模型将训练大型神经网络的碳足迹减少了一个数量级(Patterson et al., 2021)。然而,困难依然存在。
Fedus et al. (2021) 观察到,一个稀疏的1.6万亿参数模型在预训练速度上比之前的最先进模型(Raffel et al., 2019)快了4倍,但在SuperGLUE等常见基准上进行微调时却落后于较小的模型。Artetxe et al. (2021) 在MoE语言模型在域外数据上进行微调时也观察到了类似的差距。作为回应,Switch-XXL模型被提出,该模型参数较少,但计算量(FLOPs)是最大T5模型的8倍,提高了自然语言理解任务的质量。然而,必要的预训练受到之前在小规模研究中未检测到的训练不稳定性的阻碍。这些不稳定性后来在其他稀疏模型中被发现(Du et al., 2021)。这些结果揭示了参数和计算之间的必要平衡,但留下了如何可靠训练这些类型模型的开放问题。
我们在本文中的目标是提高稀疏模型的实用性和可靠性。我们研究了这两个问题,并预训练了一个2690亿参数的稀疏模型,该模型在微调时在许多竞争性NLP基准测试中实现了最先进的结果,包括SuperGLUE。我们还提出了额外的分析和设计指南(或至少是我们的启发式方法)用于稀疏专家模型。此外,这项工作强调联合优化上游预训练和下游微调指标,以避免差异(Tay et al., 2021)。
贡献
-
大规模研究稳定性技术的质量-稳定性权衡。
-
引入路由器z-loss,解决了不稳定性问题,同时略微提高了模型质量。
-
稀疏和密集模型的微调分析,突出显示了不同超参数对批大小和学习率的敏感性。我们展示了不良的超参数设置会导致微调增益几乎为零,尽管预训练速度大幅提升。
-
在分布式环境中设计帕累托高效的稀疏模型的架构、路由和模型设计原则。
-
通过专家层追踪token路由决策的定性分析。
-
一个2690亿参数的稀疏模型(稳定且可迁移的专家混合模型,ST-MoE-32B),在多种自然语言基准测试中实现了最先进的性能。

2 背景
稀疏专家模型通常用一组专家替代神经网络层,每个专家都有独特的权重(Jacobs et al., 1991; Jordan and Jacobs, 1994)。通常,层内的所有专家都是相同类型和形状的(同质),但也可以使用不同类型的专家(异质)。输入仅由一部分专家处理以节省计算,因此必须添加一种机制来确定将每个输入发送到哪里。通常,路由器或门控网络决定将输入(即单词、句子、图像块等)发送到哪里,但也提出了其他方案(Lewis et al., 2021; Roller et al., 2021; Zuo et al., 2021; Clark et al., 2022)。

最初在LSTM中提出(Hochreiter and Schmidhuber, 1997),专家层后来被Shazeer et al. (2018) 和Lepikhin et al. (2020) 用于Transformer(Vaswani et al., 2017)。Fedus et al. (2021) 的后续工作进一步简化了MoE,将token路由到单个专家(top-1),并减少了其他成本以提高训练效率。
为了提高硬件利用率,大多数稀疏模型的实现为每个专家使用静态批大小(Shazeer et al., 2017, 2018; Lepikhin et al., 2020; Fedus et al., 2021)。专家容量是指可以路由到每个专家的token数量。如果超过此容量(路由器向该专家发送了太多输入),则溢出的token将不进行计算,并通过残差连接传递到下一层。
输入token的批次 B 在数据并行维度上被分成 G 个唯一组,每组大小为 B/G。专家容量等于CF⋅⋅ tokens/experts,其中CF表示容量因子超参数,experts是专家数量,tokens是组大小。如果增加容量因子,它会创建额外的缓冲区,以便在负载不平衡的情况下减少token的丢弃。然而,增加容量因子也会增加内存和计算成本,因此存在权衡3。
最后,辅助负载平衡损失鼓励token在专家之间大致均匀分布(Shazeer et al., 2017)。这通过确保所有加速器并行处理大量数据来提高硬件效率。损失的详细信息见附录A。然而,也存在其他方法:Lewis et al. (2021) 和Clark et al. (2022) 将平衡token分配视为分配问题,并完全移除了辅助损失。

3 稳定稀疏模型的训练
稀疏模型通常比标准密集激活的Transformer更容易出现训练不稳定性(图1)。
很容易找到提高稳定性的更改,但这些更改通常以模型质量的不可接受的损失为代价(例如,使用任意小的学习率或使用严格的梯度裁剪)。我们分类并检查了几种提高稳定性的方法。稳定性技术包括对Transformer的通用修复以及特定于稀疏模型的修复:(1) 移除乘法交互 (2) 注入模型噪声 (3) 约束激活和梯度。我们最终推荐了一种新的辅助损失,路由器z-loss,它显著提高了训练稳定性,且没有质量下降。这是对Mesh Tensorflow代码库中用于最终softmax logits的z-loss的改编(Shazeer et al., 2018)。
稳定稀疏模型
-
许多方法可以稳定稀疏模型,但以质量下降为代价。
-
路由器z-loss在不降低质量的情况下稳定模型。
-
具有更多乘法组件的Transformer修改(GEGLU, RMS归一化)会降低稳定性,但会提高质量。
设计大规模稳定性研究。我们设计了一个大规模稳定性研究,稀疏模型的FLOPs与T5-XL版本(Raffel et al., 2019)相匹配,预训练在多语言语料库mC4上(Xue et al., 2020)。每个稀疏模型有32个专家,我们为每四个FFN层引入一个稀疏MoE层。训练容量因子为1.25,评估容量因子为2.0。有关本文中使用的模型的更详细描述,请参见表11。对于每种稳定性技术,我们记录稳定的比例、平均质量(英语的负对数困惑度)以及种子的标准差。
构建此研究的主要问题是小模型很少不稳定,但大不稳定模型运行足够步骤和种子的成本太高。我们发现FLOPs与T5-XL匹配的稀疏模型是良好的研究对象,因为它在大约1/3的运行中不稳定,但仍然相对便宜。此外,我们在多语言数据上运行不稳定性实验,因为我们发现这会加剧模型的不稳定性,允许我们在稍小的模型上进行实验。有关更多详细信息,请参见第9节。我们的基线配置使用六个随机种子进行训练,每个稳定性技术配置使用三个随机种子以节省计算。每个模型在mC4上预训练20k步,使用掩码语言建模目标(Fedus et al., 2018; Devlin et al., 2018)。



移除乘法交互时的稳定性与质量权衡
一些架构改进涉及更多的乘法而不是加法,或者不累积许多项。例如,矩阵乘法每个加法有一个乘法,因此我们不将其称为“乘法”操作。我们在此介绍并分析了Transformer中两个乘法交互实例的影响。
GELU门控线性单元(GEGLU)。我们的第一个例子是门控线性单元(Dauphin et al., 2017),它是两个线性投影的逐元素乘积,其中一个首先通过sigmoid函数。Shazeer (2020) 将其扩展到其他变体,并提出了GELU-Linear(Hendrycks and Gimpel, 2016)FFN层作为Transformer中通常的ReLU(Nair and Hinton, 2010)FFN的替代。

这一质量提升在后续工作中得到了证实(Narang et al., 2021)。
均方根尺度参数。我们的第二个例子是均方根(RMS)归一化中的尺度参数(Zhang and Sennrich, 2019)。在Transformer中,层不是直接连续调用的,而是有一个内部结构(称为子层调用),可以改善梯度传播和训练动态。我们的子层调用与Raffel et al. (2019) 匹配,包括:(1) RMS归一化,(2) 层调用(例如自注意力),(3) dropout(Srivastava et al., 2014),(4) 添加残差(He et al., 2015)。RMS归一化按均方根对输入向量 x∈Rd 进行逐元素缩放。然后通过乘以学习的尺度参数 g 对输出进行逐元素重新缩放。

表2显示,移除GEGLU层或RMS尺度参数可以提高稳定性,但会显著降低模型质量。我们注意到,这些尺度参数(g)对模型质量的提升与参数的其他部分(例如FFN)不成比例。与我们的发现一致,Shleifer et al. (2021) 发现向Transformer的残差连接添加学习的乘法标量会使它们更加不稳定。
在附录C中,我们进一步研究了在专家层中添加新的乘法交互的质量影响。我们发现此操作在模型步长时间几乎没有减慢的情况下提高了质量。
添加噪声时的稳定性与质量权衡
接下来,我们探讨了一个假设,即在模型中添加噪声可以提高训练稳定性(Neelakantan et al., 2015)。Taleb (2012) 认为某些系统表现出抗脆弱性,它们通过噪声改进。受此概念的启发,以及我们观察到微调(通过dropout注入噪声)很少不稳定的现象,我们研究了训练噪声是否可能提高稀疏模型的稳定性。表3显示了与基线相比的稳定性改进,但以质量下降为代价。我们还发现,Fedus et al. (2021) 引入的输入抖动在XL规模下降低了质量,因此我们在模型中将其移除。输入抖动将路由器的输入logits乘以一个在 [1−10−2,1+10−2]之间的均匀随机变量。在我们的消融中,dropout应用于整个Transformer。如前所述,小规模设置中的改进在扩展时可能无法推广,因此应始终监控趋势并在增加规模时重新评估(Kaplan et al., 2020)。
约束激活和梯度时的稳定性与质量权衡

稳定神经网络的最成功方法之一是对激活和梯度进行约束(Pascanu et al., 2013; Ioffe and Szegedy, 2015; Salimans and Kingma, 2016; Ba et al., 2016)。一种流行的方法包括裁剪梯度范数,以解决通过深层网络反向传播时的梯度爆炸问题(Pascanu et al., 2013)。
在这项工作中,我们使用Adafactor优化器,因为其内存效率高(尽管最近引入的8位优化器(Dettmers et al., 2021)可能提供更好的权衡)。Adafactor不使用梯度裁剪,而是使用更新裁剪,其中权重的变化被约束在某个范数以下。我们尝试将更新裁剪收紧到较小的值。
接下来,我们研究对进入路由器的logits的约束。路由器以float32精度(即选择性精度)计算专家的概率分布(Fedus et al., 2021)。然而,在最大规模下,我们发现这不足以产生可靠的训练。为了解决这个问题,我们引入了路由器z-loss,

选择精度格式:效率与稳定性的权衡
与大多数现代分布式Transformer一样,我们使用混合精度进行训练(Micikevicius et al., 2017)5。权重以float32存储以进行梯度更新,然后在进行前向和后向传递的矩阵乘法时转换为bfloat166。此外,所有激活都以bfloat16存储和操作,allreduce通信可以以bfloat16或float32数值精度完成。对于本工作中探索的最大模型(稍后介绍的STMoE-32B),我们发现将allreduce的数值精度减半可以加速,但这也会使训练不稳定,因此我们在整个工作中保持float32。
较低的精度格式通过减少**(a)** 处理器和内存之间的通信成本,(b) 计算成本,(c) 存储张量(例如激活)的内存,使模型更高效。然而,较低的精度格式以较大的舍入误差为代价,这可能导致不可恢复的训练不稳定性。
稀疏专家模型对舍入误差敏感,因为它们由于路由器而引入了更多的指数函数。稀疏专家模型引入了额外的指数函数——通过路由器——这可能会加剧舍入误差7并导致训练不稳定性。虽然舍入误差不会改变softmax操作中的概率顺序,但它会影响MoE中第二个token的路由,因为相对阈值(例如,只有当第二个专家的门控概率是第一个专家的1/5时,token才会被路由到第二个专家)。此外,舍入误差可能会显著改变缩放专家输出的概率——我们发现这很重要。最后,我们推测我们观察到的仅解码器模型的更高稳定性(此处未显示)是因为它们具有更少的指数函数。第9节包含更详细的讨论。
关于路由器z-loss的旁注。有人可能认为路由器z-loss是一种复杂的方法,可以用裁剪logits来替代(Wu et al., 2016)。我们解释为什么情况并非如此。目标是尽量减少进入指数函数的大舍入误差。裁剪logits发生在任何舍入误差之后——导致更大的不连续性。从某种意义上说,裁剪本身就是一种舍入误差;相反,z-loss自然鼓励模型生成绝对值较小的logits,从而更准确地建模。由于这些动态,我们确保所有指数化的张量都转换为float32。这暗示了神经网络可能更好的数字格式,因为当z-loss添加到整个网络时,未使用的指数位(见第9节)。
4 稀疏模型的微调性能
表现最好的语言模型通常通过**(1)** 在大量数据(例如互联网)上进行预训练,然后**(2)** 在感兴趣的任务(例如SuperGLUE)上进行微调来获得。有前途的新技术已经出现,包括少样本推理(Brown et al., 2020)、前缀调优(Li and Liang, 2021)、提示调优(Lester et al., 2021)和适配器模块(Houlsby et al., 2019)——然而,与微调相比,仍然存在质量差距。因此,我们在这项工作中专注于微调,但强调了稀疏模型在少样本设置中的最新成功(Du et al., 2021; Artetxe et al., 2021)。此外,我们将通过强化学习适应大型语言模型的技术留作未来工作(Ouyang et al., 2022)

假设:泛化问题
稀疏模型在大数据集的情况下表现非常出色,但在微调时有时表现不佳(Fedus et al., 2021; Artetxe et al., 2021)。我们提出了一个(并不令人惊讶的)假设,即稀疏模型容易过拟合。我们通过SuperGLUE(Wang et al., 2019)中的两个任务——Commitment Bank(De Marneffe et al., 2019)和ReCORD(Zhang et al., 2018)——来说明这个问题。Commitment Bank(CB)有250个训练示例,而ReCORD有超过100,000个。这种显著的大小差异为研究过拟合提供了一个自然的研究对象,这两个任务被选为同一基准的一部分。

在图3中,我们比较了Dense L和ST-MoE-L模型的微调特性。每个模型都在C4语料库(Raffel et al., 2019)的5000亿个token上进行了预训练。这些模型设计为与T5-Large编码器-解码器模型(Raffel et al., 2019)大致FLOP匹配,具有7.7亿参数。ST-MoE模型有32个专家,专家层频率为1/4(每四个FFN层替换为一个MoE层)。预训练和微调的容量因子为1.25,评估容量因子为2.0。我们评估了在保留的验证和训练数据集分区上的性能。
在这两个任务中,稀疏模型更快地收敛到100%的训练集准确率,支持稀疏模型在数据分布变化下有效优化。在较大的任务ReCORD上,稀疏模型的验证质量随着训练的提升而显著超过密集模型。然而,在较小的任务CB上,稀疏模型在保留数据上落后于其密集对应模型。根据Fedus et al. (2021) 的建议,我们考虑增加专家隐藏状态中的dropout(即专家dropout),但发现在这个规模下,较高的值只能适度提高质量(图4)。我们在第4.2节中研究了微调的进一步改进,并在第4.3节中研究了超参数敏感性。
微调模型参数的子集以提高泛化
为了对抗过拟合,我们尝试在微调期间仅更新模型参数的一个子集。图5测量了更新5个不同参数子集的质量:所有参数(All)、仅非MoE参数(Non MoE)、仅MoE参数(MoE)、仅自注意力和编码器-解码器注意力参数(Attention)以及仅非MoE FFN参数(FFN)。

我们观察到更新非MoE参数的效果与更新所有参数的效果大致相同,而仅更新FFN参数的效果略好。仅更新MoE参数显著降低了微调性能,而MoE参数约占模型参数的80%。仅更新非MoE参数可以有效地加速微调并减少内存。
我们假设仅微调MoE参数会导致性能不佳,因为专家层仅每1/4层出现一次,并且一个token每层最多会看到两个专家。因此,更新MoE参数将影响比我们尝试的任何其他参数子集更少的层和FLOPs。仅更新MoE参数导致的训练损失比更新非MoE参数大得多,尽管参数数量显著增加。我们进一步观察到,更新所有非MoE参数导致的训练损失比更新所有参数高,但不幸的是,这种正则化效果并没有转化为更好的验证性能。
此外,我们尝试了一种dropout变体,其中在训练期间随机屏蔽整个专家。然而,这在我们初步研究中未能提高泛化能力。附录J扩展了此实验并包含其他负面结果。
稀疏和密集模型需要不同的微调协议
稀疏和密集模型对微调协议的敏感性如何?我们研究了两个超参数:批大小和学习率。我们在C4的5000亿个token上预训练了Dense-L和ST-MoE-L,然后在SuperGLUE上进行微调。图6总结了我们的实验,完整数据见附录F中的表20。在所有超参数设置中,稀疏模型(橙色)优于密集模型(蓝色)——然而,每个模型的最佳设置可能会显著改变结果。稀疏模型受益于较小的批大小和较高的学习率。与过拟合假设(第4.1节)一致,这两个变化可能会通过增加微调过程中的噪声来提高泛化能力。最后,我们指出了在微调期间正确调整批大小和学习率的重要性。简单地使用对密集模型有效的相同微调超参数可能会掩盖稀疏模型在预训练中获得的任何改进。

稀疏模型在微调期间对丢弃的token具有鲁棒性
稀疏模型在每一层将token路由到一个或多个专家。为了使这些模型在现代硬件的SPMD范式中高效,专家容量(每个专家处理的token数量)需要提前固定(详见第2节)。当专家接收的token超过其容量时,多余的token将被丢弃——这些token不进行计算。我们再次尝试通过**(1)** 预训练时使用辅助损失来促进将相等数量的token发送到每个专家,以及**(2)** 容量因子(一个超参数)为每个专家添加额外的token空间来防止这种情况。我们尝试在微调期间关闭辅助损失并使用不同的容量因子。表5揭示了一个令人惊讶的结果,即微调质量在丢弃高达10-15%的token时没有显著影响8。对ST-MoE-32B的研究证实,高容量因子不会提高微调质量。这与Yang et al. (2021) 的发现一致,即不平衡的负载可能不会显著影响模型质量。

在微调期间插入哨兵token
哨兵token表示在跨度损坏目标中掩码的序列(Fedus et al., 2018; Devlin et al., 2018)。这与我们可能遇到的任何微调任务不同,导致预训练和微调之间的域不匹配。表6说明了这种差异。我们研究了修改微调任务以使其更像预训练任务是否会影响结果。
在表7中,我们发现添加哨兵token仅在语法错误纠正(GEC)(Rothe et al., 2021)中提高了微调质量,而在SuperGLUE中没有。我们尝试通过插入多个哨兵token(如模型在预训练期间遇到的那样)进一步减少数据分布偏移,但再次发现没有普遍的好处。然而,尽管在保留数据上没有一致的益处,我们发现密集和稀疏模型的训练收敛速度都加快了。

5 设计稀疏模型
密集模型的设计受到Kaplan et al. (2020) 的基础工作的指导。但稀疏模型提出了许多额外的问题:(1) 使用多少专家?(2) 使用哪种路由算法?(3) 容量因子的值是多少?(4) 硬件如何改变这些决策?在本节中,我们评论这些问题,并为构建帕累托高效的稀疏模型提供建议。同时,Clark et al. (2022) 提供了额外的设计建议,包括更高的层频率和top-1路由(根据Fedus et al., 2021)。
设置专家数量
第一个问题是使用多少专家。Fedus et al. (2021) 提出了Switch Transformer的缩放特性,在C4上(Raffel et al., 2019)在步骤基础上产生了单调的预训练收益,Kim et al. (2021) 提出了最多64个专家,Clark et al. (2022) 提出了最多512个专家。但随着专家数量的增加(>256)或等效地,随着模型变得非常稀疏(<1%的专家被激活),增量收益迅速减少。
然而,反思特定的硬件系统可以进一步指导这一选择。计算与内存的比率(操作强度)可以作为不同操作效率的估计(Williams et al., 2009; Shazeer, 2019)。如果加载张量到计算核心(例如ALU/MMU)的时间大大超过在张量上进行计算所需的时间,则模型是内存受限的。在现代GPU和TPU上,增加计算与内存的比率可以提高效率。
回到稀疏专家模型,每个核心使用多个专家会增加内存传输,可能会降低效率。增加专家数量不会改变完成的计算(稀疏模型对每个输入应用固定数量的计算),但会增加内存传输需求(必须从设备内存加载额外的专家变量)。这降低了计算与内存的比率9。
在我们的TPU系统上,我们建议每个核心使用一个(或更少)专家。我们最大的模型同时使用数据和模型并行,其中数据并行在“行”上,模型并行在“列”上。我们使用≤1个专家每数据并行行,以确保计算与内存的比率高,并减少评估和推理所需的核心。此外,使用更少的专家让我们可以为模型并行“列”分配更多的核心,以在模型中获得更多的FLOPs。附录H解释了当我们有比数据并行行更少的专家时的网格布局。
选择容量因子和路由算法
我们将top-1路由(Fedus et al., 2021; Roller et al., 2021)和top-2路由(Shazeer et al., 2017; Lepikhin et al., 2020)推广到研究top-n路由,其中每个token最多由n个专家处理。在本研究中,所有模型都预训练了100k步,每批1M个token,稀疏模型有32个专家,并与T5-Large(Raffel et al., 2019)FLOP匹配。我们得出了两个关键结论。

首先,增加训练和评估容量因子(CF)可以提高质量,如表8的分段块所示。例如,top-1路由在从1.0 →→ 1.25训练CF增加时提高了+0.011负对数困惑度,top-2路由在从1.25 → 2.0训练CF增加时提高了+0.009。为了提供这些数字的背景:将密集模型的大小增加三倍(从Dense-L到Dense-XL)会产生+0.090负对数困惑度的提升。因此,这些CF提升大约是密集模型提升的1/10。但这也是有代价的。增加容量因子线性增加了einsum成本、激活内存、allall通信成本和专家层的模型并行allreduce通信成本10。
其次,在固定容量因子下,top-(n+1)路由比top-n路由有小的增益(表8)。例如,在训练CF为1.25时,top-2路由比top-1路由提高了+0.004,大约是密集模型提升的1/20。这修正了Fedus et al. (2021) 的早期建议。这些实验设置之间的主要区别是计算规模。Fedus et al. (2021) 训练了220M-FLOP匹配模型,训练了50B个token。我们发现在8倍大的训练规模下(1B-FLOP匹配模型,训练了100B个token),路由到多个专家有小的增益。此外,在更大的实验规模下,top-nn与top-(n+1n+1)路由的速度差异可以忽略不计。在Fedus et al. (2021) 中观察到的速度差异是因为路由器计算占总模型计算的较大比例。

特定的硬件-软件系统将决定最佳的n和容量因子。例如,如果系统支持快速的all2all和allreduce通信,较大的容量因子和较大的n在top-n路由中可能是最优的。然而,如果all2all和/或allreduce通信较慢,较小的容量因子可能占主导地位。在我们的案例中,硬件-软件堆栈是TPU和Mesh Tensorflow。我们记录了ST-MoE-L和ST-MoE-32B模型的训练速度,如表9所示,随着训练容量因子的增加。随着模型的扩展,较高的容量因子使模型越来越慢。ST-MoE-L不需要模型并行(它适合加速器内存,这意味着没有额外的allreduce通信),使其比我们的ST-MoE-32B模型更适合高容量因子。因此,对于我们最大的模型,我们继续使用较小的训练容量因子1.25,以实现帕累托效率,与其他使用较大且更昂贵的2.0容量因子的工作不同(Lepikhin et al., 2020; Du et al., 2021)。
我们在本节中的结果集中在top-n路由上,但我们也尝试了各种其他路由技术,详见附录J。我们发现大多数表现相似或比top-n路由差。然而,我们发现Riquelme et al. (2021) 引入的批优先路由(BPR)显著帮助了容量因子小于1的性能(附录D)。我们建议BPR用于all2all和allreduce更昂贵且较低容量因子最优的较大模型。
6 实验结果
鉴于我们在训练稳定性、微调和模型设计方面的改进,我们首先验证了与T5-Large(Raffel et al., 2019)大致FLOP匹配的稀疏模型。我们通过设计和训练一个2690亿参数的稀疏模型(与320亿参数的密集模型FLOP匹配)来结束本节,该模型在广泛的NLP任务中实现了最先进的质量。
我们研究了SuperGLUE(Wang et al., 2019)基准测试,该基准测试包括情感分析(SST-2)、词义消歧(WIC)、句子相似性(MRPC, STS-B, QQP)、自然语言推理(MNLI, QNLI, RTE, CB)、问答(MultRC, RECORD, BoolQ)、共指消解(WNLI, WSC)和句子完成(COPA)和句子可接受性(CoLA)等任务。我们经常观察到SuperGLUE的良好性能与(但不保证)许多NLP任务的性能相关。我们还包括一组多样化的额外基准测试。CNN-DM(Hermann et al., 2015)和BBC XSum(Narayan et al., 2018)数据集用于衡量摘要文章的能力。问答通过SQuAD数据集(Rajpurkar et al., 2016)以及ARC Easy和ARC Reasoning Challenge(Clark et al., 2018)中的小学科学问题进行测试。如Roberts et al. (2020) 所述,我们通过在三个闭卷问答数据集上微调来评估模型的知识:Natural Questions(Kwiatkowski et al., 2019)、Web Questions(Berant et al., 2013)和Trivia QA(Joshi et al., 2017)。闭卷指的是在没有补充参考或上下文材料的情况下提出的问题。为了评估模型的常识推理能力,我们在Winogrande Schema Challenge(Sakaguchi et al., 2020)上进行了评估。最后,我们在Adversarial NLI Benchmark(Nie et al., 2019)上测试了模型的自然语言推理能力。
ST-MoE-L
为了简单起见并轻松覆盖数十个任务,我们在列出的任务的混合上进行训练,而不是单独在每个任务上微调模型。然而,由于任务的大小差异很大,按示例数量等比例采样会过度采样大任务并欠采样小任务。因此,我们按每个任务的“训练”分割中的示例数量比例混合每个任务(最多max.num_examples=65536),如Raffel et al. (2019) 所述。这意味着包含超过65536个训练示例的任务的权重与仅包含max.num_examples的任务相同。
表10总结了密集T5-Large(L)模型和稀疏模型的质量,这些模型在C4数据集(Raffel et al., 2019)上预训练了500k步,批大小为1M(524B个token)。编码器的序列长度为512,解码器的序列长度为114。我们观察到在验证(开发)集上,涵盖自然语言理解、问答和摘要的广泛任务中的改进。如Fedus et al. (2021) 所述,闭卷问答(Roberts et al., 2020)中观察到了显著的提升。
此外,支持第4.1节中提出的过拟合假设,我们观察到两个最小的任务CB和WSC(分别有250和259个训练示例)是稀疏模型没有比其密集对应模型提升的唯一任务。这再次表明,改进的稀疏模型正则化形式可能会释放更大的性能。
ST-MoE-32B
在T5-Large规模上验证了质量后,我们寻求通过ST-MoE-32B推动稀疏模型的能力。在设计时,我们寻求FLOPs和参数之间的平衡。高FLOP稀疏模型在Fedus et al. (2021) 中在我们的设置中(即编码器-解码器模型,Adafactor优化器)不稳定,但路由器z-loss使我们能够继续。为了提高计算效率,我们扩展了专家的隐藏大小(表11中的dffdff)11。最后,我们将dkvdkv增加到128,以在我们的硬件上获得更好的性能。最显著的变化是总体参数更少,每个token的FLOPs相对于Switch-C和Switch-XXL更多。我们的ST-MoE-32B“仅”有2690亿参数,并且与320亿参数的密集Transformer大致FLOP匹配。与Switch-C和Switch-XXL相比,减少的参数数量减轻了服务和微调的负担。最后,我们使用了附录C中描述的稀疏-密集堆叠。

我们在C4数据集(Raffel et al., 2019)和GLaM(Du et al., 2021)引入的数据集的混合上预训练了1.5T个token。我们使用每批1M个token,Adafactor优化器,默认超参数,以及10k步的学习率预热,然后进行逆平方根衰减。我们的模型遵循Fedus et al. (2021) 提出的初始化方案。
表12评估了我们的ST-MoE-32B模型与之前最先进的方法,使用仅推理(零样本,一次性)以及微调。在SuperGLUE上,我们的模型改进了之前的最先进模型,在测试服务器上实现了91.2的平均分数(93.2的验证准确率),比估计的人类能力高出一个百分点以上。对于两个摘要数据集,XSum和CNN-DM,我们的模型在没有对训练或微调进行额外更改的情况下实现了最先进的结果(Raffel et al., 2019; Liang et al., 2021)。ST-MoE-32B在测试服务器提交中改进了ARC Easy(92.7 → 94.8)和ARC Challenge(81.4 → 86.5)的当前最先进水平。在三个闭卷QA任务中的两个上,我们改进了之前的最先进水平。闭卷WebQA实现了47.4的准确率(之前的最佳水平为42.8,来自Roberts et al. (2020)),并超过了ERNIE 3.0 Titan 260B密集参数模型(Wang et al., 2021)的零样本性能。闭卷NatQA提高到41.9的准确率(之前的最佳水平为41.5,来自Karpukhin et al. (2020))。我们在对抗性构建的数据集(ANLI R3和WinoGrande XL)上发现了显著的改进。ANLI R3(Nie et al., 2019)将最先进水平提高到74.7(之前的最佳水平为53.4)。
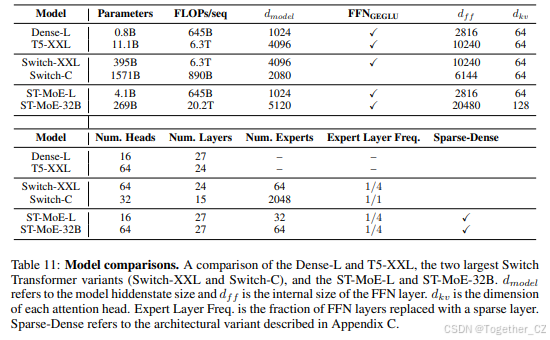
我们注意到我们模型的一些弱点。ST-MoE-32B在小型SQuAD数据集上表现不佳,准确率为90.8,低于T5-XXL设定的旧基准91.3。此外,虽然在SuperGLUE总体上设定了新的最先进水平,但某些任务,包括像CB、WSC这样的小任务,未能改进。最后,在闭卷Trivia QA上,我们的模型比Roberts et al. (2020) 的微调基线有所改进,但未能产生超过GPT-3和GLAM的增益。

虽然这不是本文的重点,但我们展示了最近在仅推理技术(如少样本学习)和微调在这些任务上的质量差异(GPT-3 Brown et al., 2020),GLAM Du et al. (2021) 和Gopher Rae et al. (2021))。正如预期和之前观察到的,微调优于零/一次性学习,但需要额外的训练和每个任务的不同模型的缺点。
7 通过模型追踪token
到目前为止,我们已经提出了定量测量和性能指标。我们改变策略,通过可视化token在专家之间的路由来探索定性特征。我们通过将一批token传递给模型并手动检查每层的token分配来实现这一点。我们考虑我们的ST-MoE-L模型在单语C4语料库(Raffel et al., 2019)或多语mC4语料库(Xue et al., 2020)上预训练。在编码器和解码器上,模型有六个稀疏层,每层有32个专家。
跨度损坏目标是恢复输入中被掩码的可变长度连续段。其格式为:
输入:I went to <<extra_id_0>> to buy <<extra_id_1>>
目标:<<extra_id_0>> the store <<extra_id_1>> milk
在我们的编码器-解码器架构中,输入将传递给编码器,目标将传递给解码器。
每组token通过负载平衡在专家之间路由,由Shazeer et al. (2017) 提出的辅助损失激励(详见附录A)。token在其组内与其他token竞争专家分配,而不是整个批次,专家专业化在很大程度上受到每组中token分布的影响。引入组的概念是为了限制将正确的token分派和收集到正确的专家的成本。

编码器专家表现出专业化
我们的第一个观察是,在每一层,至少有一个专家专门处理哨兵token(表示要填充的空白)。此外,一些编码器专家表现出明显的专业化,一些专家主要处理标点符号、动词、专有名词、计数等。表13展示了编码器专家专业化的一些显著例子。虽然我们发现了许多专业化的实例,但这些是从许多示例中特别提取的,没有明确的语义或句法专业化。
解码器专家缺乏专业化
相比之下,解码器中的专家专业化远不明显。不仅哨兵token在解码器专家之间路由得相对均匀(见表14),而且我们也没有观察到解码器专家中有意义的专业化(语义或句法)。
我们假设这种缺乏有意义的专家专业化是由跨度损坏目标引起的目标token分布造成的。特别是,(a) 由于编码器中较长的序列长度(例如,在我们的设置中,组大小为2048,而解码器中为456),解码器中联合路由的token数量较少,(b) 解码器中哨兵token的比例较高。因此,每组中的目标token通常覆盖较小的语义空间(与编码器相比),这或许解释了解码器中专家专业化的缺乏。这种架构和训练目标之间的复杂互动邀请进一步研究,以更好地利用解码器中的稀疏性和专家专业化。或者,未来的工作可以研究简单地移除解码器层中的专家,这也会在自回归解码期间带来好处(Kudugunta et al., 2021a)。

多语言专家专业化,但不按语言
接下来,我们考虑在多语言稀疏模型中预训练,该模型在多种语言的混合上训练,并检查编码器中的专家专业化。与单语情况一样,我们发现了专家专业化的有力证据。表15展示了一些专家专门处理哨兵token、数字、连词和冠词以及专有名词的例子。
人们可能期望专家按语言专业化,这似乎是划分数据批次的自然标准。然而,我们没有发现语言专业化的证据(见表15)。路由器反而将来自英语、日语、法语和中文的token不加区分地传递,专家似乎是多语言的。但考虑到token路由和负载平衡的机制,这种缺乏语言专业化的情况并不令人惊讶。由于每组token可能只包含一种或最多几种语言(在我们的设置中,一组通常由2-4个序列组成),因此所有专家都被鼓励处理所有语言的token。我们尝试了全局负载平衡损失,但这通常会导致更差的负载平衡和更差的模型性能,因此我们将进一步改进多语言专家模型留作开放工作(第9节)。

我们的可视化揭示了模型中学习的明显专业化(表13, 15)在编码器层中。其他专家专业化也在Shazeer et al. (2017) 的附录中观察到。然而,这引出了一个有趣的问题,即消除学习路由的架构(Roller et al., 2021; Zuo et al., 2021)似乎表现良好。对学习路由与随机路由的缩放特性进行广泛研究可能有助于未来工作,并帮助我们更好地理解路由行为。
8 相关工作
专家混合模型(Mixture-of-Experts, MoE)至少可以追溯到Jacobs et al. (1991); Jordan and Jacobs (1994) 的工作。在最初的概念中,MoE定义了整个神经网络,类似于集成方法。但后来Eigen et al. (2013) 扩展了将MoE作为深层网络的一部分的想法。Shazeer et al. (2017) 随后将这个想法扩展到1370亿参数的模型,以实现机器翻译的最先进水平。大多数后续工作(包括我们的工作)都遵循这种将MoE作为组件的方法。
自然语言处理中的规模。规模在自然语言处理中的显著成功(Kaplan et al., 2020; Brown et al., 2020)重新激发了MoE研究,最近的工作激增(Lepikhin et al., 2020; Fedus et al., 2021; Yang et al., 2021; Kim et al., 2021; Du et al., 2021; Artetxe et al., 2021; Zuo et al., 2021; Clark et al., 2022)。稀疏专家模型被提出作为一种更高效地实现大规模密集模型结果的方法。Fedus et al. (2021) 展示了比T5-XXL(Raffel et al., 2019)快4倍的预训练速度,Du et al. (2021) 使用1/3的能源匹配了GPT-3(Brown et al., 2020)的质量。在过去的十二个月里,多个小组实现了高效训练万亿参数深度神经网络的里程碑(Fedus et al., 2021; Yang et al., 2021; Du et al., 2021),最近,Lin et al. (2021) 引入了训练10T参数模型的技术。一个旁注是,稀疏专家模型最近的显著成功通常是在大量数据且没有分布偏移的环境中——两个例子是语言建模/跨度损坏和机器翻译(Shazeer et al., 2017; Lepikhin et al., 2020; Kim et al., 2021; Fedus et al., 2021)。相比之下,在Fedus et al. (2021); Narang et al. (2021); Artetxe et al. (2021) 中观察到了强预训练质量和差微调质量之间的差异,但我们预计正则化技术的进步将继续提高下游质量。
改进路由算法。BASE层(Lewis et al., 2021)将token路由重新定义为线性分配问题——消除了负载平衡辅助损失的需要。这项工作还展示了单专家层的有效性。Clark et al. (2022) 深入研究了少数不同路由算法的缩放特性,并提出了他们自己的BASE层变体,使用最优传输公式。Yang et al. (2021) 引入了M6-T架构和专家原型,将专家分成不同的组,并应用kk个top-11路由程序(与常用的top-kk路由形成对比)。Hazimeh et al. (2021) 提出了一个连续可微的稀疏门,展示了比普通top-kk门控的改进。其他工作(Bengio et al., 2016)考虑将路由选择作为强化学习问题。更激进的版本完全移除学习路由。Hash层(Roller et al., 2021)展示了随机固定路由(通过哈希函数)与学习路由的竞争性能。Zuo et al. (2021) 还提出了一种在训练和推理期间随机选择专家的算法,并发现比Switch Transformers提高了2个BLEU点,与Kim et al. (2021) 的较大模型竞争。最后,Fan et al. (2021) 设计了一种具有显式语言特定子层的架构(而不是像Lepikhin et al. (2020) 那样允许任意路由),以产生+1 BLEU的增益。
其他模态中的稀疏专家模型。MoE和稀疏专家模型也在语言以外的模态中推进了结果。Riquelme et al. (2021) 设计了一个150亿参数的V-MoE,以匹配ImageNet(Deng et al., 2009)的最先进模型,使用更少的计算资源。Lou et al. (2021) 同样展示了在密集视觉模型上使用MoE层在图像块和通道维度上的优势。此外,自动语音识别通过SpeechMoE变体(You et al., , )得到了改进。Kumatani et al. (2021) 在序列到序列Transformer和Transformer Transducer中使用MoE模型减少了单词错误率。
改进稀疏模型的部署。最初的专家设计(包括这项工作)在每一层分别将每个token路由到专家。一个问题是,这种类型的架构可能难以服务,因为它需要足够的内存来存储参数。Fedus et al. (2021) 展示了蒸馏是中等有效的,但最近的方法修改了路由,改为路由整个句子或任务(Kudugunta et al., ; Zuo et al., 2021),然后在服务时提取子网络(例如,仅部署与新任务相关的网络)。作为蒸馏的替代方案,Kim et al. (2021) 考虑直接修剪掉对感兴趣任务不必要的专家。
多任务学习与MoE。我们以多任务设置中的成功结束对最近MoE研究的回顾。Ma et al. (2018) 建议为每个任务使用单独的门控或路由器网络,这一想法可能很快会在Transformer架构中重新审视。最后,Gururangan et al. (2021) 建议语言模型的模块化程度更高,并根据域/任务标签或推断的标签有条件地激活专家。
9 讨论
虽然这项工作是关于稀疏模型的,但这些模型与机器学习中的许多其他有趣主题相交,如自适应计算、低精度训练、缩放原则和神经网络架构进步。因此,我们的讨论涵盖了这项研究中出现的更广泛的主题。
在多语言数据上预训练时的不可预测动态。我们经常观察到,在多语言数据上预训练的相同模型会产生较小的预训练加速,并且更不稳定。一个假设是这是由于批次中每组的序列方差。提醒一下,我们鼓励组内的token负载平衡。每组通常只有2-8个序列(更多会变得昂贵),每个序列用一种语言编写。因此,最多2-8种语言必须在专家之间平衡——即使训练超过100种语言。这导致组和批次之间的高方差,导致混乱和不可预测的路由。在后续实验中(为简洁起见仅简要提及),我们在英语C4加上一小部分微调任务的混合上进行了预训练,同样导致了不稳定的模型。
稀疏模型的鲁棒性。尽管本文专注于稀疏模型的细节,但放大来看,我们发现它们对广泛的超参数和架构变化具有鲁棒性。稀疏模型在各种路由算法、丢弃高比例token和不同超参数下都表现出色。虽然我们确实指出了在微调期间调整批大小和学习率的重要性,但我们的直觉与Kaplan et al. (2020) 一致,即真正的赢家是规模。例如,表8显示了通过简单地增加容量因子(即FLOPs)而不是更复杂的路由(即算法)可以获得更大的增益。
自适应计算。稀疏模型是自适应计算模型的一个子类,因为每个输入都应用了不同的计算。在稀疏模型中,token被路由到其选择的专家。当容量因子小于1时,模型学会不对某些token应用计算。这在计算机视觉(Riquelme et al., 2021)和我们的语言实验(附录D)中显示出了希望。我们设想未来的模型通过异质专家(例如,每个专家应用不同的计算)扩展这一点。直观地说,不同的输入示例可能需要不同数量的处理,具体取决于难度。未来的模型将通过新兴的计算基础设施(Dean, 2021)高效地实现这一目标。
从小规模到大规模推广发现。我们在整个工作中面临的一个关键问题是识别反映大规模实验的小规模模型和训练设置。这在第3节的稳定性研究中很明显,实验必须使用XL大小的模型来揭示相关动态。对于我们的架构和路由算法实验,我们经常发现当模型训练时间更长或规模更大时,改进消失,甚至逆转。一个例子是,Fedus et al. (2021) 的top-nn发现在我们这里提出的8倍大规模实验中被逆转,揭示了top-(n+1)路由比top-nn路由的小幅提升(见表8)。
以更低精度训练模型。我们发现稳定模型而不损害(有时甚至提高)质量的最佳方法是路由器z-loss。这是一种辅助损失,鼓励模型logits的绝对值较小。鉴于float32和bfloat16支持的最大数字范围(∼3e38),这使我们相信大多数范围是不需要的,压缩它实际上可能会改善模型训练动态。因此,未来的精度格式可能会考虑更压缩的指数范围来训练某些类别的模型。
设计具有更多乘法交互的新操作。第3.1节显示,具有比加法更多的乘法交互或那些不累积许多数字的操作可以提高模型性能。我们通过向专家层注入更多乘法交互进一步测试了这一点,这在不改变步长时间的情况下将预训练速度提高了4%(附录C)。我们认为这暗示了模型的有前途的架构改进,可能是一个好的设计原则。最近,深度卷积(仅累积3-5个元素)也被证明大大提高了Transformer性能(So et al., 2021)。这些操作特别令人兴奋,因为元素乘法在使用模型并行时通常不会引入任何通信开销(这使得深度卷积和我们的乘法交互非常高效)。虽然我们在第3.1节中确实注意到这些方法会增加模型不稳定性,但在我们的模型中使用路由器z-loss防止了任何进一步的不稳定性。
约束激活以缓解其他不良模型缩放动态。我们观察到了两个额外的训练不稳定性来源。(1) 编码器-解码器模型比仅解码器模型更不稳定(对于固定的FLOPs量)。编码器-解码器模型由于在解码器上每个FFN都有自注意力和编码器-解码器注意力层,因此具有更高的注意力层比例(例如,更多的指数函数)。(2) 对于固定的FLOPs量,更深的模型比更浅的模型更不稳定。更深的模型还通过额外的注意力层引入了更多的指数函数。我们假设这些观察的一个促成因素仅仅是网络中指数函数数量的增加。未来的工作可以通过向非稀疏模型的注意力softmax添加z-loss惩罚来解决这些训练动态,特别是因为我们观察到添加它们不会改变模型质量。
密集和稀疏模型对超参数的依赖不同。我们在第4.3节中的微调分析显示,密集和稀疏模型的最佳微调超参数显著不同。在某些设置中,对密集模型有效的微调超参数掩盖了稀疏模型的任何改进(尽管预训练速度大幅提升)。对于新模型类别,我们建议研究人员和从业者在过早放弃方法之前广泛测试关键超参数。
10 结论
我们通过展示一个模型,其大小是Fedus et al. (2021) 中模型的1/5,但具有更好的计算(FLOPs)与参数平衡,来缓和Fedus et al. (2021) 中对规模的过度热情。此外,这提高了稀疏模型的可用性,因为它可以以更少的内存开销部署。使用我们的稀疏模型变体,我们在广泛的竞争性公共基准测试中实现了最先进的性能。我们希望这项工作展示了模型稀疏性的力量,并加速了此类模型的采用。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










