Delta Decompression for MoE-based LLMs Compression——基于Delta解压缩的MoE架构LLMs压缩方法

本文链接：https://blog.csdn.net/Together_CZ/article/details/145876529

本文提出了一种名为 D2-MoE（Delta Decompression for MoE-based LLMs Compression） 的新型压缩框架，旨在解决混合专家（MoE）架构在大型语言模型（LLMs）中面临的存储和内存需求过高的问题。D2-MoE通过将专家权重分解为基础权重（共享部分）和Delta权重（专家特定部分），并结合费舍尔加权平均、奇异值分解（SVD）和半动态结构化剪枝等技术，实现了高效的参数压缩，同时保留了模型的性能和专家多样性。

研究背景

MoE架构通过稀疏激活机制和专家网络扩展模型容量，但其庞大的参数量和内存开销限制了其在资源受限环境中的应用。现有的压缩方法主要分为专家剪枝和专家合并两大类，但这些方法往往会导致性能下降或专家多样性的丢失。因此，如何在压缩模型的同时保留专家的特性和性能成为了一个亟待解决的问题。

研究方法

Delta分解
D2-MoE将每个专家的权重分解为基础权重（Wb）和Delta权重（∆Wi）。基础权重捕获所有专家的共享信息，而Delta权重编码专家特定的变化。这种分解方式既减少了冗余，又为Delta权重的高效压缩提供了可能。
费舍尔加权平均
为了更有效地合并基础权重，D2-MoE引入了费舍尔信息矩阵，通过计算每个专家权重的费舍尔重要性（Fi），对专家权重进行加权平均。这种方法可以优先保留重要专家的信息，同时减少冗余。
截断感知奇异值分解（SVD）
D2-MoE对Delta权重采用截断感知SVD，通过激活统计信息调整奇异值截断阈值，从而在压缩过程中保留关键信息。这种方法可以显著减少Delta权重的存储需求，同时保留其低秩结构。
半动态结构化剪枝
D2-MoE提出了一种半动态结构化剪枝策略，结合静态和动态剪枝，分别处理基础权重中的静态冗余和动态冗余。静态剪枝移除始终贡献较小的列，而动态剪枝根据输入批次实时调整剪枝策略，以适应不同的输入分布。

实验结果

D2-MoE在多种MoE语言模型（如Mixtral、DeepSeek、Phi-3.5和Qwen2）上进行了广泛的实验。实验结果表明：

在40%至60%的压缩率下，D2-MoE在语言建模和常识推理任务中均表现出显著的性能提升，相比其他压缩方法（如NAEE、MoE-I2等）平均性能提升超过13%。
在高压缩率（如80%）下，D2-MoE仍能保持较低的困惑度，并显著优于其他方法。
在推理效率方面，D2-MoE在高压缩率下实现了更高的吞吐量和更低的TFLOPs需求，展现出显著的效率优势。

D2-MoE通过创新的Delta分解和压缩策略，在保留MoE模型性能和专家多样性的同时，实现了显著的参数压缩和推理加速。该方法在多种MoE模型和任务上均表现出优越的性能，为高效部署大规模MoE模型提供了一种可行的解决方案。未来的工作可以探索将D2-MoE与其他技术（如知识蒸馏和参数量化）结合，进一步提升模型的效率和性能。这里是自己的论文阅读记录，感兴趣的话可以参考一下，如果需要阅读原文的话可以看这里，如下所示：

官方项目地址在这里，如下所示：

摘要

混合专家（Mixture-of-Experts, MoE）架构在大语言模型（LLMs）中表现出色，但其存储和内存需求巨大。为了应对这些挑战，我们提出了-MoE，一种新的delta解压缩压缩器，用于减少MoE LLMs的参数。基于对专家多样性的观察，我们将它们的权重分解为共享的基础权重和独特的delta权重。具体来说，我们的方法首先使用Fisher信息矩阵将每个专家的权重合并到基础权重中，以捕捉共享组件。然后，我们通过奇异值分解（SVD）利用其低秩特性来压缩delta权重。最后，我们引入了一种半动态结构化剪枝策略，结合静态和动态冗余分析，进一步减少参数，同时保持输入的适应性。通过这种方式，我们的-MoE成功地将MoE LLMs压缩到高压缩比，而无需额外的训练。大量实验表明，我们的方法在Mixtral、Phi-3.5、DeepSeek和Qwen2 MoE LLMs上，压缩率为40%到60%时，性能比其他压缩器高出13%以上。

关键词: 机器学习, ICML

1. 引言

近年来，大语言模型（LLMs）的进展越来越倾向于混合专家（MoE）架构，因为它们能够通过专门的专家网络扩展模型容量，同时通过稀疏激活保持计算效率。MoE的成功在最近的LLMs中显而易见，如DeepSeek-V3和MiniMax-01，这些模型在语言理解和生成任务中展示了前所未有的能力。尽管MoE LLMs具有显著的优势，但在实际部署场景中仍面临关键挑战。它们庞大的参数规模，加上存储多个专家权重的内存开销，在资源受限的环境中构成了重大障碍。

为了应对这些挑战，MoE压缩方法最近受到了广泛关注。如表1所示，当前的方法大致分为专家剪枝和专家合并方法。(1) 专家剪枝方法，以MoE-Pruner、NAEE和MoE-I为代表，实现了专家间剪枝和专家内权重稀疏化。虽然这些方法显著减少了参数，但由于专家知识的不可逆损失，通常会导致性能大幅下降。直接移除专家权重会损害模型的专门能力，通常需要额外的微调来部分恢复性能。(2) 专家合并方法则旨在将多个专家合并为更紧凑的表示。诸如EEP、MC-SMoE和HC-SMoE等方法开发了不同的加权方案，对不同专家的权重进行加权求和。虽然这些方法比直接剪枝保留了更多信息，但也引入了新的挑战。合并过程假设专家功能有显著重叠，但实际上，专家通常具有独特且互补的专业化。这导致了一个根本性的困境：权重相似的专家可以有效地合并，但那些权重不同但重要的专家则难以有效压缩，导致要么压缩比不理想，要么性能下降。这些挑战提出了一个问题：我们如何设计新的框架，超越剪枝和合并方法，在有效压缩和保留专家多样性之间取得平衡？

“多样性不是关于我们如何不同，而是关于拥抱彼此的独特性。” Ola Joseph

正如引言所述，最近的微调方法（Ping et al., 2024）量化了微调模型和原始模型之间的delta权重，以有效捕捉相似性和变化。受这些成功的启发，我们研究了是否可以在专家合并过程中回收这些被丢弃的delta权重，以保持性能而不引入过多的计算或内存开销。具体来说，我们提出了一个想法，即高效地重新分配这些被丢弃的delta权重（合并专家权重与原始权重之间的差异），以保留专家的多样性和专业化。为了探索这一点，我们进行了两个关键实验来分析MoE LLMs中专家权重的特性：(1) 我们使用中心核对齐（CKA）度量评估专家相似性。如图1所示，不同专家权重之间的相似性始终在0.3到0.5之间。这表明它们的特征空间有适度的重叠，表明虽然它们的权重某些方面可以合并，但保留专家多样性仍然至关重要。(2) 我们检查了不同专家权重分解的单值能量保留分布，如图2所示。delta权重中较大的奇异值能量保留表明，矩阵的大部分信息集中在少数奇异向量中，表明其具有强低秩结构。这表明这些delta权重可以通过低秩分解方法高效近似，而不会导致信息过度退化。这些发现表明，重新利用delta权重进行专家合并是一种有前途的MoE压缩方法，能够在效率、多样性和性能之间取得平衡。

基于这些见解，我们开发了-MoE，一种新的压缩框架，旨在解决MoE LLMs中参数冗余、内存开销和存储效率低下的挑战，同时保持模型性能和可扩展性。我们的方法不是直接移除或合并专家，而是策略性地将专家权重分解为共享的基础权重（捕捉所有专家的共性）和delta权重（编码专家特定的变化）。这种分解不仅减少了冗余，还通过利用其固有的低秩结构促进了delta权重的高效压缩。为了确保共享的基础权重准确表示专家中最关键的信息，-MoE引入了Fisher加权平均机制。该方法通过基于每个专家的Fisher重要性（量化模型参数对输入数据的敏感性）加权每个专家的贡献来计算共享的基础权重。通过优先考虑最重要专家的贡献，Fisher加权平均在冗余减少和表示保真度之间取得了平衡。为了进一步压缩delta权重，-MoE采用了一种截断感知的SVD方法，将激活统计信息整合到分解过程中。该方法根据输入激活模式调整奇异值截断阈值，确保在压缩delta权重时保留关键信息。最后，-MoE提出了对共享基础权重的半动态结构化剪枝，结合静态和动态剪枝阶段，消除冗余参数，同时实时适应输入分布。通过这些新方案，我们的D2D2-MoE具有结构化、可加速、无需额外训练、保留专家多样性和性能、并实现高压缩比等优势（见表1）。

我们广泛的实验评估突显了-MoE在多个最先进的MoE语言模型和广泛基准测试中的卓越性能。对于Mixtral-8x7B和DeepSeekMoE-16B-Base等模型，-MoE在语言建模数据集上实现了最低的困惑度，在推理基准测试中实现了最高的平均准确率，即使在高压缩率下也是如此（例如，Mixtral-8x7B在60%压缩率下的平均准确率为0.52，而NAEE为0.36）。在Phi-3.5-MoE和Qwen2-57B-A14B等大规模模型上，-MoE保持了强大的性能，提供了接近原始模型的准确率，同时显著优于等方法。-MoE在多样化的MoE LLMs和任务中的一致优越性，展示了其在保留专家专业化和任务性能的同时实现显著效率提升的普遍适用性和有效性，为MoE压缩设定了新标准。

2. 相关工作

混合专家压缩方法（见表1）减少了MoE模型中的参数冗余并最小化了存储。例如，MoE-Pruner（Xie et al., 2024）通过基于激活和路由器重要性的剪枝实现了压缩。然而，这些非结构化方法通常仅提供有限的推理加速。对于结构化剪枝，NAEE（Lu et al., 2024a）跳过非冗余专家并修剪不重要的权重连接，而（Yang et al., 2024）结合了专家间剪枝和专家内低秩分解。然而，这些方法涉及专家知识的严重损失，需要额外的微调。我们的方法与这些方法不同，避免了直接移除专家，并且不需要重新训练。专家合并方法如EEP（Liu et al., 2024a）引入了一个两阶段管道，首先剪枝专家，然后将它们合并为紧凑的表示。类似地，MC-SMoE（Li et al., 2023a）基于路由策略将专家分组，并将每个组合并为一个专家。但合并专家本质上减少了模型的多样性，可能损害其在不同输入分布上的泛化能力。HC-SMoE（Chen et al., 2024）等方法虽然减少了重新训练的需求，但仍然受限于压缩和保留模型容量之间的权衡。相比之下，我们的框架策略性地将共享知识隔离到基础权重中，同时保留专家特定的变化作为delta权重。此外，我们的半动态剪枝和其他技术也是之前方法中不存在的。

Delta压缩在LLMs中已成为减少部署多个微调模型的存储和计算成本的关键技术，通过压缩基础模型与其微调变体之间的差异（delta权重）。最近的进展，如GPT-Zip（Isik et al., 2023）和BitDelta（Liu et al., 2024b）成功地将delta权重量化为超低比特。Delta-CoMe（Ping et al., 2024）采用混合精度量化来量化分解后的delta权重的不同奇异向量。另一种方法，DeltaZip（Yao & Klimovic, 2023）开发了一个多租户服务系统，通过压缩delta权重来提供服务。与这些量化和系统级工作相比，我们不仅首次将delta压缩引入MoE压缩，还提出了新的技术，如截断感知SVD和半动态剪枝，实现了最佳的性能-效率权衡。

3. 方法论

3.1 MoE LLMs中的Delta压缩

MoE公式化。MoE架构通过使用基于专家的前馈网络（FeedForward Network, FFN）层来增强LLMs的容量和效率。MoEFFN层的输出y对于输入x的计算公式为：

其中N是专家的总数，G(x) ∈ RN表示门控权重，Ei(x)是第i个专家的输出。通过top-k选择机制实现稀疏性：

其中TopK[·]选择具有最高门控权重的k个专家，Softmax对其权重进行归一化。这导致专家的稀疏激活，从而提高效率。每个专家Ei是一个标准的FFN层，通常由两到三个全连接层组成。这些专家构成了MoE模型中的大多数权重（例如Mixtral8x7B中有96%），使它们成为压缩器（例如MC-MoE和我们的D2-MoE）的焦点。

专家Delta分解。由于存在多个专家，MoE模型高度参数化，导致专家权重之间存在显著冗余。直接压缩这些权重通常会导致性能下降，因为跨专家的共享结构没有得到充分利用。为了解决这个问题，我们引入了一种Delta压缩策略，将每个专家的权重分解为两个组成部分：一个共享基础权重，用于捕获所有专家之间的共性，以及一个Delta权重，用于编码专家特定的变化。这种分解减少了冗余，便于高效压缩，并将性能损失降至最低。设Wi ∈ Rm×n表示第i个专家的权重矩阵，其中m和n分别表示FFN层的输入和输出维度。我们将Wi表示为共享基础权重Wb和专家特定的Delta权重∆Wi之和：

在这里，Wb ∈ Rm×n是所有专家共享的，而∆Wi ∈ Rm×n代表第i个专家的独特特征。通过分离共享和专家特定的组成部分，我们确保Wb捕获共同结构，减少Delta权重∆Wi中的冗余。

3.2 专家费舍尔合并

为了有效地从专家子集K⊆{1,...,N}（大小为K=|K|）中推导出基础权重，同时保留必要的多样性，我们的目标是计算一个合并的基础权重Wb，以最小化冗余并保留下游任务所需的关键信息。传统方法，如简单平均，将合并权重计算为所有专家权重的逐元素算术平均值，表示为：

尽管简单平均在计算上是高效的，但它未能考虑不同专家的重要性差异。这可能导致基础权重Wb中关键权重的代表性不足，并增加后续阶段压缩Delta权重∆Wi的难度。为了解决这一问题，我们引入了费舍尔信息矩阵（Fisher information matrix），它在合并过程中捕捉每个专家参数的重要性。我们的合并函数使用费舍尔加权平均来计算基础权重Wb。每个专家的重要性通过费舍尔信息矩阵来量化，该矩阵测量模型参数对数据对数似然的敏感性。具体而言，第i个专家的费舍尔信息为：

其中Di表示由专家i处理的数据分布，pθ(y|x)是给定输入x的标签y的预测概率，∇θi log pθ(y|x)是相对于第i个专家的参数θi的对数似然的梯度。直观上，Fi测量梯度范数的平均大小，较高的值表明专家的参数对模型性能更为关键。利用费舍尔重要性Fi，我们计算费舍尔加权的基础权重Wb为：

在这里，Fi作为权重，放大了在合并过程中更重要的专家的影响力。通过使用费舍尔重要性的总和对权重进行归一化，我们确保合并后的基础权重保持适当的缩放比例，而Delta权重∆Wi更具紧凑性，并展现出更强的低秩特性。这便于在我们框架的后续阶段（见第3.3节）应用低秩压缩技术，如奇异值分解（SVD）。Delta权重的改进可压缩性减少了存储需求，并在推理过程中降低了内存开销。

3.3 截断感知奇异值分解

为了压缩Delta权重∆Wi，我们采用了一种截断感知奇异值分解（SVD）方法，通过引入激活统计信息增强了传统的分解方法。对于每个Delta权重∆Wi，我们首先计算其激活加权表示Wscale，如下所示：

其中Si ∈ Rn×n是从激活格拉姆矩阵XiXTi中导出的，Xi表示第i个专家的激活矩阵。具体而言，Si是通过格拉姆矩阵的Cholesky分解计算得到的。使用Wscale，我们执行SVD将其分解为三个组成部分：

其中U ∈ Rm×k和V ∈ Rn×k是正交矩阵，Σ ∈ Rk×k是一个对角矩阵，包含奇异值。然后，我们截断Σ中最小的奇异值，仅保留前k个分量。随后，压缩后的Delta U矩阵和V矩阵如下所示：

这种截断感知SVD方法减轻了由激活异常值引起的重构损失，并确保奇异值与压缩损失之间存在映射，以保留原始权重分布的关键特征，从而实现更有效的压缩过程。

3.4 半动态结构化剪枝

我们框架中的基础权重矩阵Wb代表多个专家权重的组合，使其成为满秩且具有高度表达能力。然而，其高维度引入了显著的冗余，这增加了推理过程中的存储和计算成本。传统的低秩分解或静态剪枝方法通常无法有效地压缩这些基础权重，而不会导致显著的性能下降，这是由于基础权重的独特结构导致的，它存储了来自所有专家的信息。通过经验分析，我们观察到一个关键现象：尽管基础权重矩阵中的一组列在不同输入中始终表现出微不足道的贡献（静态冗余），但其余列的相对重要性会根据输入批次显著变化（动态冗余）。这一见解促使我们开发了一种新的两阶段（先静态后动态）剪枝范式，分别处理这两种冗余：在静态剪枝阶段，我们识别并剪枝在所有输入中始终贡献最少的Wb列。为了实现这一点，我们计算了一个逐列剪枝指标，该指标结合了权重的大小及其与输入激活的相互作用。具体而言，Wb的第j列的剪枝指标计算如下：

其中Wb ∈ Rm×n，具有m行和n列（通道），X ∈ Rn×b表示大小为b的批次的输入激活。||Wb[:, j]||₂是Wb的第j列的L2范数，||X[j, :]||₂是对应于第j列的激活的L2范数。然后，我们根据剪枝指标Cj对所有列进行升序排序，并剪枝得分最低的列，以实现目标稀疏度水平的一半。在动态剪枝阶段，我们通过根据当前输入批次动态更新剩余列的剪枝指标来处理输入依赖的冗余。对于给定的输入批次X，我们重新计算逐列剪枝指标：Cdynamicj = ||Wb[:, j]||₂ · ||X[j, :]||₂，但仅针对静态剪枝后保留的列。然后，我们剪枝得分最低的列，以实现剩余一半的目标稀疏度。这种动态剪枝确保模型适应每个批次的具体输入分布，在推理过程中优化活动参数的数量。

3.5 算法总体流程

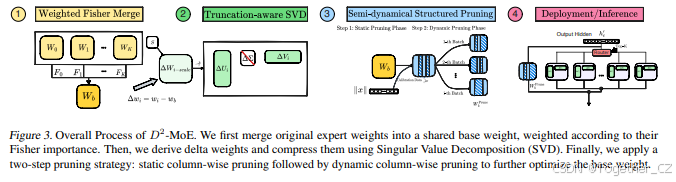
算法的总体流程总结在图3中，它概述了我们框架的主要步骤，包括费舍尔加权基础权重合并、Delta权重压缩以及基础权重的半动态结构化剪枝。在前向传播中，该过程使用稀疏门控仅激活每个输入的top-k Delta权重。例如，门控函数根据G(x)选择与top-k最相关专家的Delta权重，并将其贡献与共享基础权重一起聚合。

前向计算可以表示为：

其中∆Ui和∆Vi是选定专家的分解Delta权重。这种结构确保了高效的稀疏计算，同时利用选定专家的专业知识。

参数压缩分析。对于具有m个个体参数大小的n个专家，我们为Delta权重分配p%的压缩比，为基础权重分配s%的压缩比。对于静态参数存储，原始模型需要n·m个参数用于专家。经过Delta分解后，存储需求略有增加，变为(n + 1)m，这是由于添加了共享基础权重Wb。经过静态压缩后，存储参数可以表示为：(n·p% + s%/2)m。对于激活参数减少，原始激活存储需求是k·m，因为每次激活top-k个专家。经过压缩后，激活参数需求变为：(k·p% + s%)m。

4. 实验

在本节中，我们进行了一系列广泛的实验，以评估我们提出的D2-MoE方法的有效性。我们首先在不同的压缩率下，将我们的方法与其他最先进的压缩方法在各种MoE模型上进行比较。

为了深入了解我们方法的性能，我们还在D2-MoE上进行了详细的消融研究。所有实验均在NVIDIA A100 GPU上进行。

4.1 实验设置

模型和数据集。为了展示我们D2-MoE方法的多功能性，我们在常见的MoE模型上评估其有效性：Mixtral-8×7B、DeepSeek-moe-16b-base、Phi3.5-MoE和Qwen2-57B-A14B。Mixtral-8×7B采用8个专家，Phi-3.5-MoE具有16个专家，每个专家拥有38亿参数。相比之下，DeepSeek-moe-16b-base和Qwen2-57B-A14B采用更细粒度的专家架构，利用64个专家。我们在具有较少专家的MoE模型（如Mixtral-8x7B和Phi-3.5-MoE）以及具有更多专家的模型（如DeepSeekMoE-16BBase和Qwen2-57B-A14B）上进行实验，以展示D2-MoE的多功能性。我们在10个数据集上评估我们的方法，包括3个语言建模数据集（WikiText2（Merity et al., 2017）、PTB（Marcus et al., 1993）和C4（Raffel et al., 2020）），以及7个常识推理数据集（OpenbookQA（Mihaylov et al., 2018）、WinoGrande（Sakaguchi et al., 2020）、HellaSwag（Zellers et al., 2019）、PIQA（Bisk et al., 2020）、MathQA（Amini et al., 2019）、ARC-e和ARC-c（Clark et al., 2018））。我们在零样本设置中使用LM-Evaluation-Harness框架（Gao et al., 2023）对这些数据集进行评估。

实现细节。为了公平比较，我们使用WikiText-2中的512个随机样本作为校准数据进行所有实验。我们专注于在不重新训练模型参数的情况下进行模型压缩。更多细节见附录A。

4.2 压缩性能与比较

多种MoE LLMs的主结果。 表2展示了D2-MoE在不同MoE模型和压缩率下的优越性能。在Mixtral-8×7B上，20%压缩时，D2-MoE平均得分为0.60（达到原始性能0.63的95.2%），优于NAEE（0.58）和MoE-I2（0.57）。即使在60%的高压缩率下，我们的方法仍保持0.52的竞争力，显著优于基线（0.36）。这种优势在具有更多专家的模型上进一步验证。对于DeepSeek-MoE-16B-Base，我们的方法在20%、40%和60%的压缩率下分别达到0.54、0.49和0.41的平均得分，显著优于基线方法，尤其是在WikiText-2、PTB和C4的困惑度指标上，我们的方法比MoE-I2表现更好。在Phi-3.5-MoE和Qwen2-57B-A14B上也观察到类似的优越性能，这表明D2-MoE在不同模型规模下均能有效保持性能。

与其他压缩器的比较。 表3展示了我们在Mixtral-8×7B上20%压缩率下与多种压缩方法的比较结果。D2-MoE在多个指标上均优于现有的压缩方法，包括剪枝方法（SparseGPT、NAEE）、基于SVD的方法（ASVD、MoE-I2）以及混合方法（LoSparse、MC-SMoE、MoE-Compress）。D2-MoE在保持95.2%原始性能（平均得分0.60）的同时，在WikiText-2（4.65）、PTB（16.32）和C4（8.59）的困惑度指标上表现出色，优于纯剪枝方法。在下游任务中，D2-MoE在推理任务（如ARC-e和WinoG）中表现出色，优于所有基线方法。尽管混合方法（LoSparse和MC-SMoE）在性能上表现出显著下降，尤其是在困惑度指标上，而我们的方法在所有评估维度上均保持稳定性能。这一全面比较验证了D2-MoE在保持所需压缩率的同时，有效保留了模型能力，实现了模型效率与性能之间的最佳平衡。

推理加速和内存减少。 表4展示了不同方法在高压缩率（60%、70%和80%）下对Mixtral-8×7B模型的推理效率。D2-MoE在保持最低TFLOPs的同时，实现了最高的吞吐量。在60%压缩率下（186.8亿参数，34.8GB内存），D2-MoE实现了277.72 tokens/sec的吞吐量，仅需481 TFLOPs，与NAEE的计算效率相当，但吞吐量高出2.1%。相比之下，MoE-I2和LoSparse需要更高的计算资源（分别为838和1150 TFLOPs），但吞吐量更低。随着压缩率的提高，D2-MoE的效率优势更加明显。在80%压缩率下（93.3亿参数，17.3GB内存），我们的方法实现了313.29 tokens/sec的吞吐量，分别比NAEE和MoE-I2高出12.5%和6.5%，而LoSparse尽管使用了4.6倍的TFLOPs（1330），但吞吐量仅为198.04 tokens/sec。与此同时，D2-MoE在WikiText-2上的困惑度分别为6.35、8.15和12.95（60%、70%和80%压缩率），即使在极端压缩水平下，也显示出逐渐且可控的性能下降。这些结果表明，D2-MoE不仅实现了更好的压缩质量，还提供了实际的推理速度和计算效率优势，使其特别适合于对模型大小和推理速度都有严格要求的实际部署场景。

4.3 消融研究

基础权重的不同合并方法。 表5探讨了不同基础权重合并方法的性能，验证了我们提出的费舍尔合并方法的有效性。与均值平均、基于专家频率的平均（Li et al., 2023b）、RegMean（Jin et al., 2022）和TIES（Yadav et al., 2024）等其他基础权重合并技术相比，我们的费舍尔合并方法通过从不同专家中选择性提取重要权重并将其整合到基础权重中，实现了最低的困惑度得分。例如，在Mixtral-8×7B模型上，40%压缩率下，我们的方法在WikiText-2（5.28）、PTB（20.54）和C4（10.10）上均优于其他方法。

基础权重和Delta权重的不同压缩方法。 表6展示了基础权重和Delta权重的不同压缩方法。对于基础权重，我们的动态剪枝方法表现出色，在WikiText-2（5.28）、PTB（20.60）和C4（10.12）数据集上均优于截断感知SVD（使用SVD-LLM中的缩放矩阵）和静态剪枝（Wanda-sp）。对于Delta权重，我们比较了剪枝、不使用缩放矩阵的普通SVD和激活感知SVD（Yuan et al., 2023a）。我们的截断感知SVD方法（使用缩放矩阵）表现最佳。因此，我们在D2-MoE中使用半动态剪枝处理基础权重，使用截断感知SVD处理Delta权重。

压缩率超参数的敏感性。 表7展示了基础权重和Delta权重压缩率之间的敏感性。在Mixtral-8×7B模型40%压缩率的设置下，我们观察到基础权重的压缩率较低通常可以实现更好的性能，因为它保留了更多跨专家的关键信息并保持了模型的准确性。然而，基础权重的压缩率与推理时间加速之间存在权衡，因为较高的基础权重压缩率通常会导致更快的推理速度，但可能会降低性能。经过仔细评估，我们选择了一个平衡的比率，以优化性能和推理效率之间的平衡。

通过Delta权重修剪扩展D2-MoE。 图4展示了Delta权重修剪对D2-MoE性能的影响。随着修剪的增加，困惑度逐渐上升，但我们的方法在不同压缩率（43%-81%）下均保持了竞争力。例如，在43%压缩率下，我们在WikiText-2上实现了6.43的困惑度，与非修剪压缩模型相当。即使在75%压缩率下（修剪7个专家），困惑度仍保持在14.71，表明我们的方法在压缩和性能之间实现了有效的平衡。

校准数据的影响。 表9展示了校准数据的选择（无论是WikiText-2还是C4）对整体任务性能的影响较小，突显了我们方法在多样化数据集上的鲁棒性。表9还探讨了校准样本数量的变化对性能的影响。结果表明，增加数据样本数量通常会降低困惑度，表明随着样本数量的增加，性能有所提升。

5. 结论

在本研究中，我们提出了D2-MoE，这是一个用于压缩基于MoE的LLMs的统一框架，通过解决其权重结构中的固有冗余问题来实现。我们的方法系统地整合了Delta分解、费舍尔加权合并、截断感知奇异值分解（SVD）和半动态结构化剪枝，以实现高效的参数减少，同时保持MoE模型的性能。通过将专家权重分解为共享基础权重和专家特定的Delta权重，我们有效地隔离了共同结构并减少了冗余。我们的实证分析表明，D2-MoE在基准任务上实现了显著的参数压缩，同时保留了MoE模型的预测性能。未来的研究可能会探索将D2-MoE与先进的训练技术（如知识蒸馏和参数量化）相结合。我们希望所提出的框架能够为大规模建模的效率提升做出贡献，并为在实际应用中部署高容量MoE模型提供一条可行的路径。

局限性：我们的D2-MoE涉及一些复杂的分解和剪枝步骤（更多分析见附录A.4）。我们计划在未来的工作中简化这一过程。

本研究的主要关注点是开发和评估用于改进MoE LLMs存储和推理效率的技术方法。通过解决MoE架构中的固有冗余问题，我们的D2-MoE框架为设计绿色且易于使用的LLMs做出了贡献。所有评估和实验均在公开可用的基准测试上进行，确保了透明性和可复现性。我们相信，我们的框架在伦理影响和社会影响方面不会引发争议。