[信号处理]小波分析学习心得第一篇_脉冲信号与母函数的相似度-CSDN博客

本文链接：https://blog.csdn.net/UMENGSI/article/details/135458932

作为信号处理方向的一枚萌新，这篇文章主要介绍了信号分析上的一些应用，也是记录近一段时间学习心得，希望道友和同好们和谐指正，共同交流学习、变得更强！

【看山是山】

小波分析的应用是与小波分析的理论研究紧密地结合在一起的。现在，它已经在科技信息产业领域取得了令人瞩目的成就。现在，对于其性质随时间是稳定不变的信号，处理的理想工具仍然是傅立叶分析。但是在实际应用中的绝大多数信号是非稳定的，而特别适用于非稳定信号的工具就是小波分析。

小波分析的应用领域十分广泛，具体应用方面上有数学领域的许多学科；信号分析、图像处理；量子力学、理论物理；军事电子对抗与武器的智能化；计算机分类与识别；音乐与语言的人工合成；医学成像与诊断；地震勘探数据处理；大型机械的故障诊断等方面，它包括：

1. 数学领域的许多学科：用于数值分析、构造快速数值方法、曲线曲面构造、微分方程求解、控制论、进行函数的逼近和插值等；

2. 医学成像方面：减少B超、CT、核磁共振成像的时间，提高分辨率等；

3. 信号分析、图像处理：在信号分析方面的滤波、去噪声、压缩、传递等；在图像处理方面的图像压缩、分类、识别与诊断，去污等。

这里主要从信号分析角度展开：

1. 时频分析

小波变换可以用于信号的分解和重构，提取信号的时频特征，并对信号进行多尺度细化分析。小波变换的出现是为了解决短时傅里叶变换时域分辨率和频率分辨率的矛盾，即变换基函数，这部分参见《1. 信号分析角度：凭什么！小波变换比短时傅里叶变换更优秀？》。

（1）STFT短时傅里叶变换

最后一个是cwt。注：不过这里CWT的频率对不上，希望评论区大佬可以指点一下。

（2）CWT连续小波变换

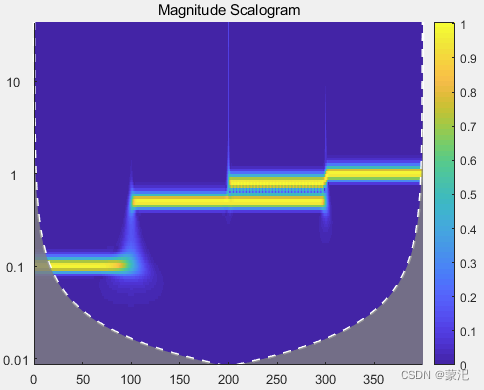
关于连续小波变换的边缘效应和影响锥可以参考这篇博文 .

clc;clear all;close all;
fs = 1e5;%采样频率
n=10000;

f1 = 1e2; f2 = 5e2; f3 = 8e2; f4 = 1e3;
t = (0:n-1)/fs;

sig1 = cos(2*pi*f1*t);
sig2 = cos(2*pi*f2*t);
sig3 = cos(2*pi*f3*t)+cos(2*pi*f2*t);
sig4 = cos(2*pi*f4*t);

sig = [sig1,sig2,sig3, sig4];

% sig=sig1+sig2+sig3+sig4;
for i=1:length(sig)-1
    t(i+1)=t(i)+1/fs;
end
figure(1);
subplot(511);plot(t,sig);
title("时域信号")

%% 短时傅里叶变换
Nw=1024;%窗口长度对短时傅里叶变换的影响不言而喻，窗口大则频域分辨率越高，相应的时间上分辨率下降
window = hamming(Nw);%使用window将信号划分为段并执行 开窗
noverlap = Nw/2;%窗重叠，使用相邻的重叠之间的noverlap个样本片段。
f_len = Nw/2 + 1;
f = linspace(0, 2e3, f_len);%返回f中指定的循环频率处的STFT
[s, f, tt, p] = spectrogram(sig, window, noverlap, f, fs);%短时傅里叶变换
hold on
subplot(512);imagesc(tt, f, p);xlabel('Time'); ylabel('Freqency');
c = colorbar;
c.Label.String = 'Power Spectral density()';%功率谱是反映单位频带内信号功率随频率的变化情况，也就是信号功率在频域内的分布情况--功率谱密度就是功率谱除以采样频率,单位：被测物理量单位^2/Hz
title("STFT:窗口1024")


Nw=2048;%窗口长度对短时傅里叶变换的影响不言而喻，窗口大则频域分辨率越高，相应的时间上分辨率下降
window = hamming(Nw);%使用window将信号划分为段并执行 开窗
noverlap = Nw/2;%窗重叠，使用相邻的重叠之间的noverlap个样本片段。
f_len = Nw/2 + 1;
f = linspace(0, 2e3, f_len);%返回f中指定的循环频率处的STFT
[s, f, tt, p] = spectrogram(sig, window, noverlap, f, fs);%短时傅里叶变换
hold on
subplot(513);imagesc(tt, f, p);xlabel('Time'); ylabel('Freqency');
c = colorbar;
c.Label.String = 'Power Spectral density()';%功率谱是反映单位频带内信号功率随频率的变化情况，也就是信号功率在频域内的分布情况--功率谱密度就是功率谱除以采样频率,单位：被测物理量单位^2/Hz
title("STFT:窗口2048")

Nw=4096;%窗口长度对短时傅里叶变换的影响不言而喻，窗口大则频域分辨率越高，相应的时间上分辨率下降
window = hamming(Nw);%使用window将信号划分为段并执行 开窗
noverlap = Nw/2;%窗重叠，使用相邻的重叠之间的noverlap个样本片段。
f_len = Nw/2 + 1;
f = linspace(0, 2e3, f_len);%返回f中指定的循环频率处的STFT
[s, f, tt, p] = spectrogram(sig, window, noverlap, f, fs);%短时傅里叶变换
hold on
subplot(514);imagesc(tt, f, p);xlabel('Time'); ylabel('Freqency');
c = colorbar;
c.Label.String = 'Power Spectral density()';%功率谱是反映单位频带内信号功率随频率的变化情况，也就是信号功率在频域内的分布情况--功率谱密度就是功率谱除以采样频率,单位：被测物理量单位^2/Hz
title("STFT:窗口4096")

%% 连续小波变换
hold on
subplot(515)
[wt,ff,coi] = cwt(sig,'morse',fs);
imagesc(t,ff,abs(wt));xlabel('Time'); ylabel('Freqency');
c = colorbar;
c.Label.String = 'Power Spectral density()';%功率谱是反映单位频带内信号功率随频率的变化情况，也就是信号功率在频域内的分布情况--功率谱密度就是功率谱除以采样频率,单位：被测物理量单位^2/Hz

figure
cwt(sig,'morse',fs);

Continuous 1-D wavelet transform - MATLAB cwt- MathWorks 中国This MATLAB function returns the continuous wavelet transform (CWT) of x.https://ww2.mathworks.cn/help/wavelet/ref/cwt.html

从对一个外行解释的角度，分析一下什么是小波分析？ - 知乎本专栏中讲了很多时频域分析的知识，不过似乎还没有讲过时频域分析是怎样引出的。所以本篇将回归本源，讲…https://www.zhihu.com/question/19725983/answer/3292925962

2. 滤波去噪

小波变换可以用于信号去噪，通过将信号分解为小波系数，并去除噪声的小波系数，再重构信号，可以实现信号的去噪处理。

最经典的莫过于小波包分析：小波包分解（Wavelet Packet Decomposition），又称为最优子带树结构（Optimal Subband Tree Structuring）正是对小波变换的进一步优化。其主要的算法思想是：在小波变换的基础上，在每一级信号分解时，除了对低频子带进行进一步分解，也对高频子带进行进一步分解。最后通过最小化一个代价函数，计算出最优的信号分解路径，并以此分解路径对原始信号进行分解。这个可以单独说一期了。简单看一下它的最优小波包树图吧。

1992年由Ronald R. Coifman and Mladen Victor Wickerhauser 在《Entropy-Based Algorithms for Best Basis Selection》提出。

信号被小波包切成了一段一段的频带，这样就可以用一些指标去衡量每个频段包含的有用信息，进而将有用的频段筛选出来。这里特征指标的选择也是研究的一个热点（刨个坑）。这里用的是幅值能量。

信号的分解和重构，也就是在这个过程中便完成了滤波去噪。

[wpt]=wpdec(signal,3,'dmey','shannon');  %小波包分解，3代表分解3层，'dmey'使用meyr小波
plot(wpt)               %画小波包树图
wpviewcf(wpt,1);        %画出时间频率图

% 1-范数：就是norm(...,1)，即各元素绝对值之和；2-范数：就是norm(...,2)，即各元素平方和开根号；
sNod = read(wpt,'sizes',[7,8,9,10,11,12,13,14]);
cfs7=wpcoef(wpt,7);%对重排序后第3层0节点的小波包系数0-625Hz
cfs8=wpcoef(wpt,8);%对重排序后第3层0节点的小波包系数626-1250Hz
cfs10=wpcoef(wpt,10);%对重排序后第3层0节点的小波包系数1876-2500Hz
cfs9=wpcoef(wpt,9);%对重排序后第3层0节点的小波包系数1251-1875Hz
cfs13=wpcoef(wpt,13);%对重排序后第3层0节点的小波包系数3751-4375Hz
cfs14=wpcoef(wpt,14);%对重排序后第3层0节点的小波包系数4376-5000Hz
cfs12=wpcoef(wpt,12);%对重排序后第3层0节点的小波包系数3126-3750Hz
cfs11=wpcoef(wpt,11);%对重排序后第3层0节点的小波包系数2501-3125Hz

E_cfs3_1=norm(cfs7,2)^2;
E_cfs3_2=norm(cfs8,2)^2;
E_cfs3_3=norm(cfs9,2)^2;
E_cfs3_4=norm(cfs10,2)^2;
E_cfs3_5=norm(cfs11,2)^2;
E_cfs3_6=norm(cfs12,2)^2;
E_cfs3_7=norm(cfs13,2)^2;
E_cfs3_8=norm(cfs14,2)^2;
E_total=E_cfs3_1+E_cfs3_2+E_cfs3_3+E_cfs3_4+E_cfs3_5+E_cfs3_6+E_cfs3_7+E_cfs3_8;

p_node(1)= 100*E_cfs3_1/E_total;           % 求得每个节点的占比
p_node(2)= 100*E_cfs3_2/E_total;           % 求得每个节点的占比
p_node(3)= 100*E_cfs3_3/E_total;           % 求得每个节点的占比
p_node(4)= 100*E_cfs3_4/E_total;           % 求得每个节点的占比
p_node(5)= 100*E_cfs3_5/E_total;           % 求得每个节点的占比
p_node(6)= 100*E_cfs3_6/E_total;           % 求得每个节点的占比
p_node(7)= 100*E_cfs3_7/E_total;           % 求得每个节点的占比
p_node(8)= 100*E_cfs3_8/E_total;           % 求得每个节点的占比
figure;
x=1:8;

bar(x,p_node);%条形图
title('各个频段能量所占的比例');
xlabel('频率 Hz');
ylabel('能量百分比/%');
for j=1:8
    text(x(j),p_node(j),num2str(p_node(j),'%0.2f'),...
        'HorizontalAlignment','center',...
        'VerticalAlignment','bottom')
end

3. 数据压缩

小波变换具有很好的数据压缩效果，可以将数据转换为小波系数，通过去除冗余信息，实现数据的压缩和稀疏表示。（实操貌似和滤波去噪一样，最著名的是Daubechies女士的SSWT《Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool》），后续学习了再更新(刨个坑)。

【看山不是山】

要真正理解这一切，我们需要深入小波分析的数学原理。

1. 信号分析角度：凭什么！小波变换比短时傅里叶变换更优秀？

关于从傅里叶变换进化到小波分析，这些文章和视频写的很详细，给予我学习上也有很大的帮助，我会列在行文最后，感谢开源精神！

这里我做一些关键性总结：

如前边所说，小波做的改变就在于，将无限长的三角函数基换成了有限长的会衰减的小波基

从公式可以看出，不同于傅里叶变换，变量只有频率ω，小波变换有两个变量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函数的伸缩，平移量 τ控制小波函数的平移。尺度就对应于频率（反比），平移量 τ就对应于时间。

从这里开始，我会从学习中困惑我的点说起，首先给出几个我觉得特别重要的概念：

(1). 小波基函数（母小波（小波函数）和父小波（尺度函数））；(2).小波变换系数（近似分量和细节分量）；

小波基函数

母小波：就是小波基函数（母函数）通过改变伸缩、平移两个参数，即 $\phi((t-b)/a)$ ，而得到的所有基函数的函数，因此以这一组尺度函数来代表原来的信息。母小波是一个高通滤波器，用于提取信号的高频成分，也称为细节分量。比如haar小波、Db小波。小波函数： $\phi(x)=\sum_{k=0}^{M-1}b_k\phi(2x-k)$ 。b_k称为小波系数。

父小波：尺度函数，是信号在某一尺度下的近似。父小波是一个低通滤波器，用于提取信号的低频成分，也称为近似分量。尺度函数， $\psi(x)=\sum_{k=0}^{N-1}a_k\phi(2x-k)$ 。a_k称为尺度系数。

关于母小波和父小波的深入理解要看《2.泛函分析角度》，这里从信号分析角度理解：

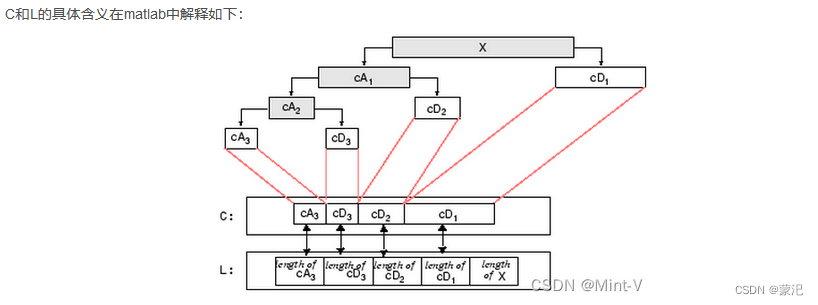
在MATLAB小波工具中可以通过滤波器将信号分解成低频子带（cA3）和高频子带（cD3/cD2/cD1）。前面说了，母小波相当于一个高通滤波器，父小波相当于一个低通滤波器。从信号处理的角度去总结，小波变换就是将信号在频域上由低频子带和高频子带表示（尺度函数是表示低频信息，小波函数表示高频信息）。那么各子带中是什么呢？

小波变换系数

小波分析是对基函数(小波)与原函数相似度的度量，计算出的系数，是尺度（频率或时间）的函数，表示该函数在特定尺度上与子小波的接近程度。小波变换后的系数比较大，就表明了小波和信号的波形相似程度较大；如果小波变换仅仅反映信号整体的近似特征，往往选用较大的尺度；反映信号细节的变换则选用尺度不大的小波。理解了这句话，就理解了cA和cD里面是什么了。

但是小波变换系数是怎么计算来的呢？另外，都说小波函数族是由母小波变换而来，我在学习中也困惑过母小波的伸缩和平移到底是怎么变化的？

这里引用这个大佬的图，画的很形象！

我们重点看中间的小波的图像，它在时间轴上进行平移，然后频率也在改变，这也对应了母小波的在由频率而伸缩和由时间而平移的变化而得到的小波函数族。同时，每平移一次进行一次卷积运算，计算结果在第三张图上按照对应的时间（由位置决定）和频率（由尺度决定）画出计算结果。仔细观察小波的变换，可以发现其特点：高频部分具有较高的时间分辨率和较低的频率分辨率，而低频部分具有较高的频率分辨率和较低的时间分辨率，这就恰好解决了STFT的痛点。这一回答了小标题的疑惑。

总结一下：对一个给定信号进行小波变换,就是将该信号按某一小波函数簇展开，即将信号与一系列不同尺度和不同时移的小波函数在频域上乘积(即时域上卷积)，生成小波系数。同一尺度下所有不同时移的小波函数的线性组合称为信号在该尺度下的小波分量。同时，当我们在每个尺度下都平移着和信号乘过一遍后，我们就知道信号在每个时间位置都包含哪些频率成分，即时频信息。

https://youtu.be/jnxqHcObNK4https://youtu.be/jnxqHcObNK4 小波的原理和应用_数字图像处理中的小波分析原理及应用场景-CSDN博客文章浏览阅读243次。小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的，通过物理的直观和信号处理的实际需要经验的建立了反演公式，当时未能得到数学家的认可。与傅里叶变换在整个时间范围内对信号进行分析相比，小波变换可以根据信号的不同部分选择不同的基函数，从而更准确地描述信号的局部特征。小波，也被称为小波变换或离散小波变换，是一种在时间和频率领域内对信号或数据进行分析的方法。5．信号去噪：小波变换可以用于信号去噪，通过将信号分解为小波系数，并去除噪声的小波系数，再重构信号，可以实现信号的去噪处理。_数字图像处理中的小波分析原理及应用场景https://blog.csdn.net/ahah12345678/article/details/133970422

小波分析的起源、发展与应用_小波分析的发展历史-CSDN博客文章浏览阅读2.2w次。小波分析 (wavelet Analysis) 是 20 世纪 80 年代中期发展起来的一门数学理论和方法，由法国科学家 Grossman 和 Morlet 在进行地震信号分析时提出的，随后迅速发展。 1985 年 Meyer 在一维情形下证明了小波函数的存在性 , 并在理论上作了深入研究。 Mallat 基于多分辨分析思想，提出了对小波应用起重要作用的Mallat算法，它在小波分析中的地位相当_小波分析的发展历史https://blog.csdn.net/chenyusiyuan/article/details/1876282#:~:text=%E4%BA%8B%E5%AE%9E%E4%B8%8A%E5%B0%8F%E6%B3%A2%E5%88%86%E6%9E%90%E7%9A%84,%E6%B1%82%E8%A7%A3%E3%80%81%E6%8E%A7%E5%88%B6%E8%AE%BA%E7%AD%89%E3%80%82

小波变换理论及应用综述_一阶同步压缩小波变换 morlet小波-CSDN博客文章浏览阅读9.2k次，点赞27次，收藏88次。简介：本学习的课程中我们学习了八种常见的变换方式，除了这八种常见的变换方式，在工程上也有一些实际应用的变换方式，本文将从对于频谱的分析入手对于小波变换的理论和应用进行一定的介绍。关键词：小波变换，频谱新雅书院智能工程与创意设计卢旭洋 2018013441 §01 为什么需要小波变换？1.1 傅里叶变换的不足傅里叶变换常用于分析信号的频谱，对于平稳的信号来说，傅里叶变换会非常清晰地显示出信号的频率。以y(t)=sin⁡(30πt)+sin⁡(40πt)y\left(._一阶同步压缩小波变换 morlet小波https://blog.csdn.net/zhuoqingjoking97298/article/details/118367095

小波分析 - 搜索结果 - 知乎知乎，中文互联网高质量的问答社区和创作者聚集的原创内容平台，于 2011 年 1 月正式上线，以「让人们更好的分享知识、经验和见解，找到自己的解答」为品牌使命。知乎凭借认真、专业、友善的社区氛围、独特的产品机制以及结构化和易获得的优质内容，聚集了中文互联网科技、商业、影视、时尚、文化等领域最具创造力的人群，已成为综合性、全品类、在诸多领域具有关键影响力的知识分享社区和创作者聚集的原创内容平台，建立起了以社区驱动的内容变现商业模式。https://www.zhihu.com/search?type=content&q=%E5%B0%8F%E6%B3%A2%E5%88%86%E6%9E%90

2. 泛函分析角度：小波变换中的高频分量和低频分量，到底是谁？

下面吃点硬菜，不过泛函俺们也没深入系统学过，综合各路大佬的文章，这里列出来，当做笔记用吧。

正如先问所说，真正理解小波理论的正交完备性、多分辨分析、理解母小波和父小波，要从数学的角度去看：在小波变换中，一个位于希尔伯特空间中的函数，可以分解成一个尺度函数和一个小波函数，其中尺度函数对应原始函数中的低频部分，小波函数对应原始函数中的高频部分。通过尺度函数可以构建对原始信号的低通滤波器，通过小波函数可以构建对原始信号的高通滤波器。

为了理解这句话，我们可以深入去看这些教材和文章。。。

[1]Ruch D K , Fleet P V . Wavelet Theory: An Elementary Approach with Application[M]. John Wiley & Sons, 2009.

[2] Ingrid Daubechies. 小波十讲 [M]. 国防工业出版社 , 2004.

小波分析 – Dezeming Familyhttps://dezeming.top/?page_id=1019 从泛函分析看小波分析的发现(一)--Haar小波 - 知乎学习泛函分析以后，如同怀孕10个月必须要分娩一样，小波分析是一定要生出来了，不生出来就会憋死人，因此小波的出生平凡而又简单，这是学习泛函分析，将函数放在 L^2[a,b] 希尔伯特空间中思考以后的必然产物。我们…https://zhuanlan.zhihu.com/p/405177439

这个大佬用三章介绍了从泛函角度看小波分析，倒是看的我直犯困，确实很硬核。

【看山还是山】

窥一斑而知全豹，知道了这些，也算是入门了。但是真正理解透小波变换，这些还差得很远。

不说小波基函数正交性、能量有限性、稀疏性、多分辨率这些性质在数学上怎么推导来的，只是稍微去检索一下，便可知道，除了离散/连续小波变换、小波包变换、还有同步压缩小波变换、经验小波变换、可调Q小波变换、小波散射卷积网络，为图像处理而诞生出的脊波(Ridgelet)变换、曲波(Curvelet)变换、轮廓波(Contourlet)变换...光理解他们的名字就有够费神的了。但也正是这么纷繁复杂的小波宇宙，推动着人类科技的一步步前。向Morlet，Grossmann，Meyer，Daubechies，
Mallat前辈...致敬！！！这是笔者第一次写这样的文章，也是督促自己可以在这条路上走得更远、更扎实。

关于小波，Morlet，Grossmann，Meyer，Daubechies，Mallat - 知乎转自：未来数学家，向大佬致敬。匈牙利电子工程师丹尼斯·加博尔（Dennis Gabor）1946年提出加窗傅里叶变换，开创了在时间-频率平面上分析信号的方法，Gabor还发明了全息摄影术，这项工作让他获得了1971年的诺贝尔…https://zhuanlan.zhihu.com/p/625292103

小波分析这种信号处理方法是不是过时了，对于含有噪声的非平稳声信号，目前最流行的处理方法是什么？ - 知乎非平稳信号处理应该是现在信号处理技术最新的也是最热的研究方向了，信号处理方法从最早的时域统计到傅里…https://www.zhihu.com/question/23701194/answer/167005497