Huffman赫夫曼编码的工作原理

谈到压缩这玩意儿，大家可能会想到 忘记压缩密码 将巨大文档变成一个神秘的小文件，而且你还通过这个小文件来恢复这个巨大文档。但是，大家一定都想过，为什么压缩能这么神奇呢？

 

首先抛开那些什么二叉树，二分查找的。假如让人帮忙复述这一段话：

 

•  

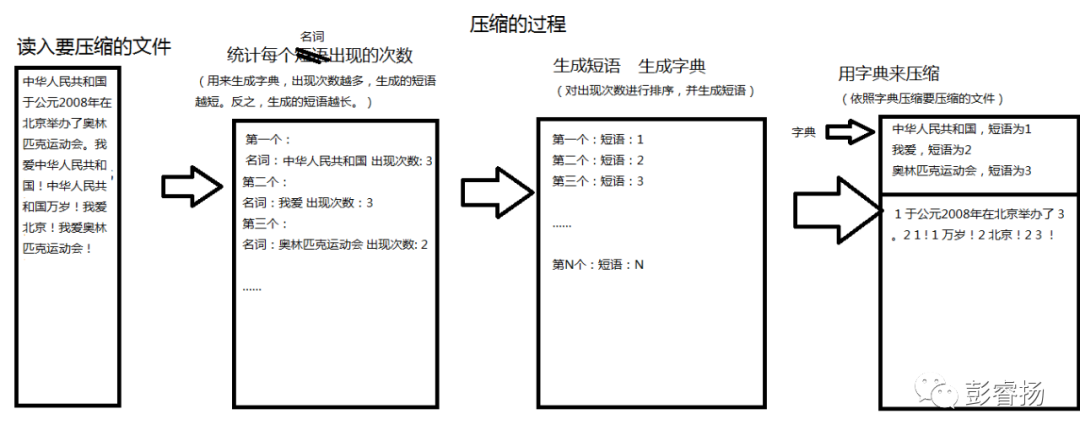
中华人民共和国于公元2008年在北京举办了奥林匹克运动会。

 

他可能会说成：

 

•  

中国2008年在北京举办了奥运会。

 

一下子短了将近一半！这是怎么回事儿啊？

 

我们都知道，中国就是指中华人民共和国，奥运会就是指奥林匹克运动会。而公元2008年，即使不加公元，人们也会明白你的意思。所以，这其实就是用一些固定的短语（例如中国）来替代比较长的名词（中华人民共和国）。这种方法在压缩算法中叫做字典。

 

但是，让机器来做这件事就难多了，因为机器对什么汉语英语一窍不通，更不知道什么中国美国。他无法理解短语、句子，连字是什么他也不关心。所以，我们要想让机器能恢复你的大文档，就必须给他一本厚厚的‘字典’ （当然，机器也不喜欢背字典），这本字典中包含着这个文档中用到的名词，以及比这个名词更短的短语。所以，压缩文件中的内容实际上是：

 

•  

字典 和 被字典替换过的新句子（比原句子更短）

 

而字典看起来像是这样：

 

•  
•  
•  
•  
•  
•  
•  

第一个: 短语: 中国  对应的名词: 中华人民共和国
第二个: 短语: 奥运会  对应的名词: 奥林匹克运动会
......

 

因为机器不理解短语，不关心名词，我们也可以在短语上做点手脚，让他变得更短。机器最喜欢的是数字，所以，我们可以将短语都替换成数字。这时候，字典变成了这样：

 

•  
•  
•  
•  
•  
•  
•  

第一个: 短语: 1   对应的名词: 中华人民共和国
第二个: 短语: 2   对应的名词: 奥林匹克运动会
......

 

所以，我们可以对照着字典，将原来很长的句子替换成这个：

 

原句（真长）：

•  

中华人民共和国于公元2008年在北京举办了奥林匹克运动会。

 

字典：

•  
•  
•  
•  
•  
•  
•  

第一个: 短语: 1   对应的名词: 中华人民共和国
第二个: 短语: 2   对应的名词: 奥林匹克运动会
......

 

替换后：

•  

1 于公元2008年在北京举办了 2。

 

好像有点复杂，其实也没什么难的。在我们进入什么完全二叉树、二进制位前先消化一下：

 

 

（如果大家有不懂的地方，可以在后台直接问我，我收到消息后会慢慢慢慢回复。）

 

 

大家了解了基本知识，现在我们来解析一下压缩算法中的元老——huffman编码吧。

 

 

huffman编码的核心思想有两个，一个是刚才我们了解的字典，一个是二叉树。

 

二叉树可以想象成一棵倒过来的树，他由树枝和树叶组成，每一个树枝树叶上都有一个数字。

 

每一根树枝上可以有树枝，也可以有树叶。但是，同一根树枝上树枝树叶的总和不能大于二，换句话说，一根树枝上最多只能有两个东西（或者叫做节点 node，节点泛指树枝树叶。）

 

父节点是有孩子的，他是一根树枝，子节点是指父节点的孩子，他既可以是树枝也可以是树叶。

 

啊，是不是晕了？看张图片吧。

 

 

为什么要设计成这个样子呢？

 

大家有没有玩过猜数字游戏（就是《Python编程：从入门到实践》那本书所说的作者小时候做的游戏），程序从1-100之间找一个随机数，然后让你猜，并告诉你猜的太大、太小或者猜对了。大家试试玩这个游戏，找一下最快的方式。

 

 

最快的方式类似于这样：

 

 

没错，这就是二叉查找——每次寻找范围中间的那个数字，并且不断比较，最终找到结果。二叉树是为查找而生的，他的查找速度很快，完全是二叉查找的功劳。

 

说的太远了，我们继续回来说huffman编码。

 

huffman编码会先初始化一个字典，这是一个表格，里面有名词以及他的出现次数。他读取出要被压缩的文件，并填完这个表格。

 

然后，他按出现的次数由大到小排列一个列表，里面只有名词的内容。

 

最关键的一步，他将出现次数最大的作为根节点，第二大的是根节点左边的孩子节点，第三大的是根节点右边的孩子节点。

 

第四大的是第二大的左边的孩子节点，还是画张图片吧。

 

 

huffman怎么分配短语呢？是这样的，他按照每个位来编码，根节点的编码为1，根左节点的编码为11，根右节点的编码为10（注意是二进制数），etc.

 

 

所以，我们用huffman编码将最开始那句话编码下，就变成了：

 

•  

1 于公元2008年在北京举办了 2 。3 1 ！1 万岁！3 北京！3 2 ！

 

后面是字典。。。 

 

压缩算法绝对不止huffman一种，这是一种十分简单的算法，相信大家看了这篇文章，应该都懂了吧……（没有自信的）