用 * 输出一个正六边形,输入一个整数 n 代表输出的正六边形的边的长度 (*的数目)
代码::
n = int(input("input n:"))
for i in range(n, 2 * n):
if i <= 2 * n - 1:
print((2 * n - 1 - i) * ' ', end='')
print(i * ' *')
a = 1
for i in range(2 * n - 2, n - 1, -1):
while i >= 2:
print(a * ' ', end='')
a += 1
break
print(i * ' *')


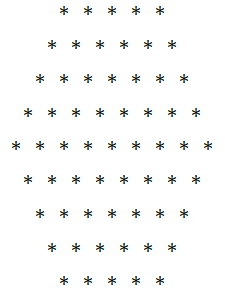
























 1178
1178

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








