HDU 5735 Born Slippy（树形DP）

Description
一个n个节点的有向树，每个点有点权w[i]，对于每个节点s=1,2,…,n，需要找一个序列v[1],v[2],…,v[m]满足：
1.v[1]=s，v[i]是v[i-1]的祖先，i=2,…,m
2.最大，其中opt为AND,OR,XOR之中的一种
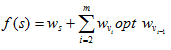
求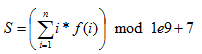
Input
第一行一整数T表示用例组数，每组用例首先输入点数n和操作opt，然后输入n个整数wi表示n个点的点权，之后n-1个整数fi表示点fi是点i的父亲节点
(T<=300,2<=n<=2^16,0<=wi<=2^16)
Output
对于每组用例输出一个整数S
Sample Input
3
5 AND
5 4 3 2 1
1 2 2 4
5 XOR
5 4 3 2 1
1 2 2 4
5 OR
5 4 3 2 1
1 2 2 4
Sample Output
91
139
195
Solution
令dp[x]=f(x)-w[x]，则较容易得到转移方程dp[x]=max{dp[y]+w[x] opt w[y]}，其中y是x祖先，注意到0<=w[i]<=2^16，将数字划分为前八位和后八位，对每个点x，用f[a][b]表示w[x]前八位为a，后八位opt b+dp[x]的最大值，那么每次转移求dp[x]时，若w[x]前八位为a，后八位为b,则有dp[x]=max{ f[i][b]+(i opt b)<<8 }，其中i是x所有祖先的权值前八位，这个可以在dfs的时候用vis数组标记下得到，得到dp[x]之后，因为之后的dfs中需要更新f[a][i]的值，所以此处令开一个数组temp[x][i]记录一下f[a][i]，回溯的时候还原即可，而更新f[a][i]就是令f[a][i]=max{ f[a][i], dp[x]+b opt i }，i=0,1,…,255，所以每次更新dp数组和f数组的复杂度都是O(255)，树形DP复杂度O(n)，总时间复杂度为O(255n)
Code

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
typedef unsigned int u;
#define Max(x,y) (x>y?(x):(y))
#define mod 1000000007ll
#define maxn 258
u T,n,w[maxn*maxn],f[maxn][maxn],temp[maxn*maxn][maxn],vis[maxn];
ll ans;
vector<int>v[maxn*maxn];
char op[5];
u opt(u a,u b)
{
    if(op[0]=='A')return a&b;
    else if(op[0]=='X')return a^b;
    return a|b;
}
void dfs(int x)
{
    u a=w[x]>>8,b=w[x]&255;
    ll dp=0;
    for(int i=0;i<256;i++)
        if(vis[i])dp=Max(dp,f[i][b]+(opt(i,a)<<8));
    vis[a]++;
    ans=(1ll*x*(dp+w[x])%mod+ans)%mod;
    for(int i=0;i<256;i++)
        temp[x][i]=f[a][i],f[a][i]=Max(f[a][i],dp+opt(b,i));
    for(int i=0;i<v[x].size();i++)
        dfs(v[x][i]);
    vis[a]--;
    for(int i=0;i<256;i++)f[a][i]=temp[x][i];
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        ans=0;
        memset(vis,0,sizeof(vis));
        for(int i=1;i<=n;i++)v[i].clear();
        scanf("%d%s",&n,op);
        for(int i=1;i<=n;i++)scanf("%d",&w[i]);
        for(int i=2;i<=n;i++)
        {
            int j;
            scanf("%d",&j);
            v[j].push_back(i);
        }
        dfs(1);
        printf("%I64d\n",ans);
    }
    return 0;
}