HDU 5737 Differencia（归并树）

Description
给两个长度均为n的序列a和b，对这个序列做m次操作，每次操作是将a序列某一段区间的所有数改成同一个值，问每次操作后满足a[i]>=b[i]的i的个数
Input
第一行为一整数T，对于每组用例首先输入四个整数n,m,A,B,之后两行每行n个整数分别表示a序列和b序列，m次操作通过以下子函数得到
int a = A, b = B, C = ~(1<<31), M = (1<<16)-1;
int rnd(int last) {
a = (36969 + (last >> 3)) * (a & M) + (a >> 16);
b = (18000 + (last >> 3)) * (b & M) + (b >> 16);
return (C & ((a << 16) + b)) % 1000000000;
}
其中last为上一次查询的答案，初始化为0，每次操作令c=rnd()%n+1,d=rnd()%n+1,x=rnd()+1，若c+d+x是奇数则将a序列中区间[c,d]中所有数改成x，若c+d+x为奇数，则查询有多少i满足a[i]>=b[i]
(1<=n<=100000,1<=m<=3000000,1<=A,B<=2^16,1<=ai,bi<=10^9)
Output
对于每组用例，记z[i]为第i次操作后的答案，每次修改后的答案是0，求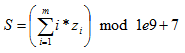
Sample Input
3
5 10 1 2
5 4 3 2 1
1 2 3 4 5
5 10 3 4
5 4 4 2 1
1 2 3 4 5
5 10 5 6
5 4 5 2 1
1 2 2 4 5
Sample Output
81
88
87
Solution
归并树，将b序列放到线段树上，每个节点上存的是将这个节点代表的在b序列中的某一段排完序后的有序表，例如5 3 4 1 2就会形成下面这样的树

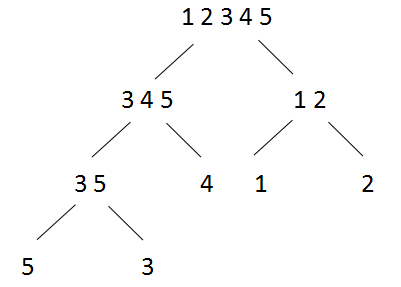
对于线段树上每个节点i，用st[i]和en[i]表示这个节点在b序列中的位置，换句话说，线段树每个节点上存的是b[st[i]]~b[en[i]]排完序后的结果
再将线段树上这些有序表按后序遍历的顺序放在pool数组中，例如上图那例子对应的pool数组就是5 3 5 3 4 3 4 5 1 2 1 2 1 2 3 4 5
然后对pool数组中每个数pool[i]，用pl[i]和pr[i]表示在pool[i]所在节点的左儿子和右儿子中,最后一个不大于pool[i]的点在pool数组中的下标，例如上例中，对pool[15]=3来说，他所在节点的两棵子树为3 4 5和1 2，分别对应pool数组的下标为6 7 8和11 12，所以pl[i]=6，pr[i]=12，如果左(右)子树所有数都大于pool[i]则令pl[i] (pr[i]) =0
那么每次对于一次修改，首先在st[1]~en[1]中二分搜索出最后一个不大于x的数的位置pos，那么两个子节点的有序表中最后一个不大于x的数的位置就是pl[pos]和pr[pos]，依次类推我们可以得到线段树每个节点所代表的有序表中最后一个不大于x的数的位置pos，那么某个节点i对答案的贡献就是pos-st[i]+1，这样每个节点的权值更新就变成了O(1)（此处节点的权值表示这个节点所代表的b序列子段对答案的贡献），每次更新和修改操作就是O(log n)，总时间复杂度O(mlog n)
Code

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
#define mod 1000000007ll
#define ls (t<<1)
#define rs ((t<<1)|1)
#define maxn 111111 
int T,n,m,a[maxn],b[maxn],c,d,x,cnt,ans,res;
//c,d是每次操作区间,cnt为线段树上有序表点数和,ans记录总答案,res记录每次查询的答案 
int st[maxn*3],en[maxn*3];
//线段树中第i个节点上的有序表是b[st[i]]~b[en[i]]排完序后的结果 
int pool[maxn*17];
//pool数组是将线段树上每个节点的有序表按后序遍历放在一起的结果
//例如b数组为1 2 3 4 5时,pool数组就是1 2 1 2 3 1 2 3 4 5 4 5 1 2 3 4 5 
int pl[maxn*17],pr[maxn*17];
//pl[i]和pr[i]表示在pool[i]所在节点的左子树和右子树中,最后一个不大于pool[i]的点在pool数组中的下标  
int lazy[maxn*3];//lazy标记 
int num[maxn*3];//num[i]表示sigma{a[i]>=b[i],i=st[i],...,en[i]} 
void Build(int t,int l,int r)
{
    lazy[t]=-1;
    if(l==r)
    {
        st[t]=++cnt,en[t]=cnt;
        pool[cnt]=b[l];
        num[t]=(a[l]>=b[l]);
        return ;
    } 
    int mid=(l+r)>>1;
    Build(ls,l,mid),Build(rs,mid+1,r);
    num[t]=num[ls]+num[rs];
    int l1=st[ls],r1=en[ls],l2=st[rs],r2=en[rs];
    st[t]=cnt+1;
    while(l1<=r1&&l2<=r2)
        pool[++cnt]=pool[l1]<=pool[l2]?pool[l1++]:pool[l2++];
    while(l1<=r1)pool[++cnt]=pool[l1++];
    while(l2<=r2)pool[++cnt]=pool[l2++];
    en[t]=cnt;
    l1=st[ls],l2=st[rs];
    for(int i=st[t];i<=en[t];i++)
    {
        while(l1<=r1&&pool[l1]<=pool[i])l1++;
        while(l2<=r2&&pool[l2]<=pool[i])l2++;
        pl[i]=l1-1,pr[i]=l2-1;
        if(pl[i]<st[ls])pl[i]=0;
        if(pr[i]<st[rs])pr[i]=0;
    }
}
void Lazy(int x,int pos)
{
    num[x]=pos?pos-st[x]+1:0;
    lazy[x]=pos;
}
void Push_down(int t)
{
    if(lazy[t]==-1)return ;
    int pos=lazy[t];
    Lazy(ls,pl[pos]),Lazy(rs,pr[pos]);
    lazy[t]=-1;
}
void Update(int t,int l,int r,int pos)
{
    if(c<=l&&d>=r)
    {
        Lazy(t,pos);
        return ;
    }
    Push_down(t);
    int mid=(l+r)>>1;
    if(c<=mid)Update(ls,l,mid,pl[pos]);
    if(d>mid)Update(rs,mid+1,r,pr[pos]);
    num[t]=num[ls]+num[rs];
}
void Query(int t,int l,int r)
{
    if(c<=l&&d>=r)
    {
        res+=num[t];
        return ; 
    }
    Push_down(t);
    int mid=(l+r)>>1;
    if(c<=mid)Query(ls,l,mid);
    if(d>mid)Query(rs,mid+1,r);
    num[t]=num[ls]+num[rs];
}
int Binary_search(int x)
{
    int l=st[1],r=en[1],ans=0,mid;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(pool[mid]<=x)ans=mid,l=mid+1;
        else r=mid-1;
    }
    return ans;
}
int A,B,C=~(1<<31),M=(1<<16)-1;
int rnd() 
{
    A=(36969+(res>>3))*(A&M)+(A>>16);
    B=(18000+(res>>3))*(B&M)+(B>>16);
    return (C&((A<<16)+B))%1000000000;
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        ans=cnt=res=0;
        scanf("%d%d%d%d",&n,&m,&A,&B);
        for(int i=1;i<=n;i++)scanf("%d",&a[i]);
        for(int i=1;i<=n;i++)scanf("%d",&b[i]);
        Build(1,1,n);
        for(int i=1;i<=m;i++)
        {
            c=rnd()%n+1,d=rnd()%n+1,x=rnd()+1;
            if(c>d)swap(c,d);
            if((c+d+x)&1)Update(1,1,n,Binary_search(x));
            else
            {
                res=0;
                Query(1,1,n);
                ans=(1ll*i*res%mod+ans)%mod;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}