洛谷 P2703 [NOI2006] 千年虫

最新推荐文章于 2024-07-24 20:44:05 发布

honkkengn

最新推荐文章于 2024-07-24 20:44:05 发布

阅读量758

点赞数 20

文章标签：算法 c++ 图论数据结构动态规划

本文链接：https://blog.csdn.net/VF222/article/details/140634082

版权

题目描述

千年虫是远古时代的生物，时隔几千万年，千年虫早已从地球上销声匿迹，人们对其知之甚少。考古生物学家最近开始对其有了兴趣，因为一批珍贵的千年虫化石被发现，这些化石保留了千年虫近乎完整的形态。

理论科学家们根据这些化石归纳出了千年虫的一般形态特征模型，并且据此判定出千年虫就是蜈蚣的祖先！但科学家 J 发现了实际与理论的一些出入，他仔细的研究了上百个千年虫化石，发现其中大部分千年虫的形态都不完全符合理论模型，这到底是什么因素造成的呢？理论科学家 K 敏锐的指出，千年虫的形态保存在化石中很有可能发生各种变化，即便最细微的变化也能导致它不符合模型。

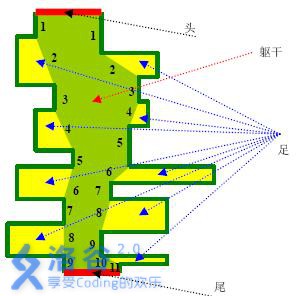
于是，摆在科学家面前的新问题诞生了：判断一个化石中的千年虫与理论模型的差距有多大？具体来说，就是根据一个千年虫化石的形态 �A，找到一个符合理论模型的形态 �B，使得 �B 是最有可能在形成化石时变成形态 �A。理论学家提出的“千年虫形态特征模型”如下（如左图所示）：躯体由头、尾、躯干、足四大部分构成。

头，尾用一对平行线段表示。称平行于头、尾的方向为 �x 方向；垂直于 �x 的方向为 �y 方向；
在头尾之间有两条互不相交的折线段相连，他们与头、尾两条线段一起围成的区域称为躯干，两条折线段都满足以下条件：拐角均为钝角或者平角，且包含奇数条线段，从上往下数的奇数条垂直于 �x 方向。
每条折线段从上往下数的第偶数条线段的躯干的另一侧长出一条足，即一个上、下底平行于 �x 方向的梯形或矩形，且其中远离躯干一侧的边垂直于 �x 方向。

注意：足不能退化成三角形（即底边的长度均大于零），躯干两侧足的数目可以不一样。（如上图，左边有 44 条足，右边有 55 条足）

可见，�x-�y 直角坐标系内，躯干和所有足组成的实心区域的边界均平行或垂直于坐标轴。为了方便，我们假设所有这些边界的长度均为正整数。因此可以认为每个千年虫的躯体都由一些单位方格拼成。每个单位方格都由坐标 (�,�)(x,y) 唯一确定。设头尾之间的距离为 �n，则我们可以用 2×�2×n 个整数来描述一条千年虫 �B（如右图）：将 �B 沿平行 �x 轴方向剖分成 �n 条宽度为 11 的横条，每个横条最左边一格的 �x 坐标设为 ��Li，最右一格的的 �x 坐标设为 ��Ri。则 (�,�1,�2,…,��,�1,�2,…,��)(n,L1,L2,…,Ln,R1,R2,…,Rn) 就确定了一条千年虫。

由于岁月的侵蚀，在实际发现的化石中，千年虫的形状并不满足上面理论模型的规则，一些格子中的躯体已经被某些矿物质溶解腐蚀了。地质、物理、生物学家共同研究得出：

腐蚀是以格子为单位的，只能一整格被腐蚀；
腐蚀是分步进行的，每一步只有一格被腐蚀；
如果去掉一个格子后躯体不连通了，那么这个格子当前不会被腐蚀；
如果一个格子的左边邻格和右边邻格都还没被腐蚀，那么这个格子当前不会被腐蚀；
与头相邻的格子不能全部被腐蚀，与尾相邻的格子不能全部被腐蚀。

倘若满足上面五条，我们仍然可以用 (�,�1,�2,…,��,�1,�2,…,��)(n,L1,L2,…,Ln,R1,R2,…,Rn) 来描述一个化石里头的千年虫的形态。其中 ��≤��Li≤Ri。

例如下图：

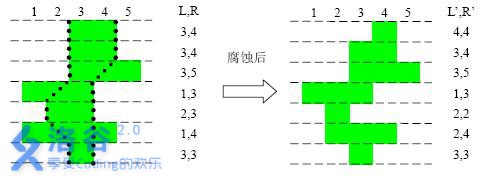
现在你的任务是，输入一个化石里的千年虫的描述 �A，找一个满足理论模型的千年虫的描述 �B，使得 �B 可以通过腐蚀过程得以变为 �A，且由 �B 转化为 �A 的代价（须被腐蚀的格子数）最少。输出此最小代价。

输入格式

第一行为一个整数 �n。

以下 �n 行，每行两个整数，其中第 �i 行为两个整数 ��′Li′、��′Ri′，用一个空格分开；保证输入数据合法。

输出格式

仅一行，为一个整数，表示最少代价。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

【样例说明】

如图：

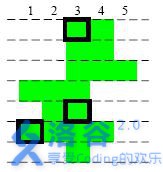
【评分方法】

本题没有部分分，你的程序的输出只有和我们的答案完全一致才能获得满分，否则不得分。

【数据范围】

对于 30%30% 的数据，�≤100n≤100，��≤100Ri≤100；

对于 50%50% 的数据，�≤1000n≤1000，��≤1000Ri≤1000；

对于 70%70% 的数据，�≤105n≤105，��≤1000Ri≤1000；

对于 100%100% 的数据，1≤�≤1061≤n≤106，0≤��≤��≤1060≤Li≤Ri≤106。

我们注意到这个题本质是给定一个序列 ��ai，然后需要给每个 ��ai 加上一个非负整数得到序列 ��bi，使得最后的序列满足这样的条件：

可以将整个序列分成奇数段，使得一段内的数都相等，且相邻两段之间满足 <,>,<,...><,>,<,...> 的关系。即形成谷，峰，谷，峰...，谷这样的形式。

然后要最小化加上的数的和。

做法什么的可以看别的题解，这里主要证明一下结论。

结论是一定存在一组最优的 ��bi 满足对于任意 �i，∃�,∣�−�∣≤2,��∈[��,��+1]∃j,∣i−j∣≤2,bi∈[aj,aj+1]（网上写的结论是 [��,��+2][aj,aj+2]，我是证的过程中发现结论实际上更强。）

我们首先考虑一下如果每段长度都是 11（即相邻两数都不相等），那么有显然的结论：若 �i 在谷，那么 ��=��bi=ai，若 �i 在峰，那么 ��=max⁡(��,��−1+1,��+1+1)bi=max(ai,ai−1+1,ai+1+1)。因为一个谷的位置我们一定不会给它加，而峰的位置只要加到比相邻两数大即可。

然而现在麻烦的地方在于段长度不为 11 的时候。

我们的思路是先随便考虑一个合法的解，然后来改造它使得代价不增并使它满足一些特殊的性质。

对于一个 ��=��bi=ai 的位置，我们称它为固定点，对于一个 ��∈[��,��+1]bi∈[ai,ai+1] 的位置，我们称它为弱固定点。

下面讨论的段都是长度 >2>2 的段。

首先考虑段的两端，对于谷，若它某一端不是固定点，那么可以让这个数减一，段中与它相邻的数加一。对于峰，若它某一端里面一个数不是固定点，那么可以让这一端加一，里面那个数减一。

然后考虑段的内部。

对于谷，我们考虑找到内部相邻的三个位置，满足中间的位置不是弱固定点。那么我们可以让中间这个位置减二，其他两个位置加一。

对于峰，我们考虑找到内部相邻的三个位置，满足两边的位置都不是固定点。那么我们可以让中间这个位置加二，其他两个位置减一。

画画图就可以知道我们的这些操作都不改变解的合法性。不停地做这些操作，直到无法操作时，可以发现对于长度 >2>2 的段内部的数都满足上面提到的结论了。

然后我们把同一段看作一个数，它新的值 ��′ai′ 是段内 ��ai 的 max⁡max。这时我们发现一段 [�,�][l,r] 的 ��′ai′ 满足 ��′=max⁡(��,��+1)=max⁡(��−1,��)ai′=max(al,al+1)=max(ar−1,ar)

因为对于长度为 22 的段显然，而长度大于 33 的段经过上面的操作一定在与端点距离 ≤1≤1 的位置存在固定点。

我们现在只关心长度为 22 的段..那么谷显然满足结论，因为 ��=max⁡(��,��+1)ai=max(ai,ai+1) 或 max⁡(��−1,��)max(ai−1,ai)，而对于长度为 22 的段构成的峰，如果这个峰取到了自己的 �′a′，那么满足条件，否则仍然有一点棘手。

我们现在约定这个峰被它右边的谷限制。即右边的 �′a′ 比较大。那么看起来当右边的谷长度为 22 时，峰中的左元素与谷中的固定点会相距 33..当然证到这里仍然得到了取值个数为常数，只不过稍微弱了一点。但是我们并不满足。

考虑如果峰中的右元素不是固定点，那么我们可以让峰中的右元素减一，谷中的左元素加一，此时峰的长度就减一，变成长度为 11 的峰。此时因为原来满足 �=�′+1b=a′+1，容易发现仍然满足条件。做不了这个操作的峰一定满足右元素是固定点，那么就满足性质了。（这里注意一下每次我们操作完之后段的形态会变化，我们需要重新求 �′a′ 然后得到新答案）

我们来总结一下：

长度为 11 谷：��=��bi=ai

长度为 22 谷：∃�,∣�−�∣≤1,��=��∃j,∣i−j∣≤1,bi=aj

长度 >2>2 谷：∃�,∣�−�∣≤1,��=��∃j,∣i−j∣≤1,bi=aj 或 ��∈[��,��+1]bi∈[ai,ai+1]

长度为 11 峰：∃�,∣�−�∣≤2,��∈[��,��+1]∃j,∣i−j∣≤2,bi∈[aj,aj+1]

长度为 22 峰：∃�,∣�−�∣≤1,��=��∃j,∣i−j∣≤1,bi=aj

长度 >2>2 峰：∃�,∣�−�∣≤1,��=��∃j,∣i−j∣≤1,bi=aj

综上，对于任意 �i，∃�,∣�−�∣≤2,��∈[��,��+1]∃j,∣i−j∣≤2,bi∈[aj,aj+1]。

#include<bits/stdc++.h>
using namespace std;
const int N=1000000+10;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef double ddf;
int n,m;
int l[N],g[N],f[2][N][2],pr,nt;
int t[2],s[2][N];
int ass;
void fuck(){
	memset(f,0x3f,sizeof(f));
	t[1]=0;
	for(int j=1;j<=3;j++){
		for(int k=g[j];k<=g[j]+2;k++){
			if(k>=g[1])s[1][++t[1]]=k;
		}
	}
	for(int i=1;i<=t[1];i++)f[1][i][0]=s[1][i]-g[1];
	pr=0,nt=1;
	for(int i=2;i<=n;i++){
		pr^=1,nt^=1;t[nt]=0;
		int lf=max(1,i-2),rf=min(n,i+2);
		for(int j=lf;j<=rf;j++){
			for(int k=g[j];k<=g[j]+2;k++){
				if(k>=g[i])s[nt][++t[nt]]=k;
			}
		}
		for(int j=1;j<=t[nt];j++){
			f[nt][j][1]=f[nt][j][0]=inf;
			for(int k=1;k<=t[pr];k++){
				if(s[pr][k]>s[nt][j])f[nt][j][0]=min(f[nt][j][0],f[pr][k][1]);
				else if(s[pr][k]<s[nt][j])f[nt][j][1]=min(f[nt][j][1],f[pr][k][0]);
				else f[nt][j][0]=min(f[nt][j][0],f[pr][k][0]),f[nt][j][1]=min(f[nt][j][1],f[pr][k][1]);
			}
			f[nt][j][0]+=s[nt][j]-g[i];
			f[nt][j][1]+=s[nt][j]-g[i];
		}
	}
	int re=inf;
	for(int i=1;i<=t[nt];i++)re=min(re,f[nt][i][0]);
	ass+=re;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d%d",&l[i],&g[i]);
	fuck();
//	cout<<ass<<endl;
	for(int i=1;i<=n;i++)g[i]=N-l[i];
	fuck();
	printf("%d",ass);
	return 0;
}

拜拜!

honkkengn

关注

20
点赞
踩
10

收藏

觉得还不错? 一键收藏
0
评论
洛谷 P2703 [NOI2006] 千年虫

我们首先考虑一下如果每段长度都是 11（即相邻两数都不相等），那么有显然的结论：若 �i 在谷，那么 ��=��bi=ai，若 �i 在峰，那么 ��=max⁡(��,��−1+1,��+1+1)bi=max(ai,ai−1+1,ai+1+1)。结论是一定存在一组最优的 ��bi 满足对于任意 �i，∃�,∣�−�∣≤2,��∈[��,��+1]∃j,∣i−j∣≤2,bi∈[aj,aj+1]（网上写的结论是 [��,��+2][aj,aj+2]，我是证的过程中发现结论实际上更强。
复制链接

扫一扫