数据结构：树与二叉树（二） 二叉树

这篇文章讲一下二叉树ADT。

1.二叉树数据结构

（1）二叉树（Binary Tree）是一个有限元素的集合（可以空），它或者是空（空二叉树），或者由一个称为根的元素以及分别称为左子树和右子树的两个互不相交的集合组成，这个两个集合又都是二叉树。

上面这个定义太绕口了，我读了好几遍才明白，二叉树，说白了就是每个结点最多只有两个孩子结点（即孩子结点数量<=2）。

（2）二叉树有五种形态，第一种是空二叉树，第二种是只有父亲结点，第三种是只有做孩子，第四种是只有有孩子，第五种是既有左孩子又有右孩子，如下图所示：

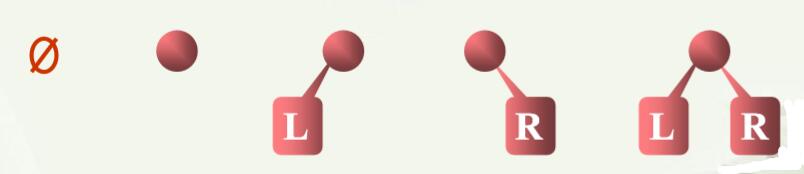
（3）二叉树结构化定义

 

2.二叉树的性质

（1）第一个性质：二叉树第i层上最多有2^(i-1)个结点(i>=1)，最少，除根节点外，自然是零个结点最少。

（2）第二个性质：深度为k的二叉树，至多有2^k-1个结点，最少有零个结点。

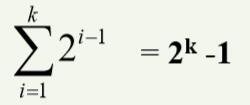
（3）第三个性质：对任意一棵二叉树T，如果其叶子结点数为n，度为2的结点数为m，则n=m+1.

这里还有个证明，我简单给大家写一下：

证明：

设度为1的结点数为k，总结点数为s，

那么s=n+m+k

设分支数为B，则B=s-1=n+m+k-1

又因为B=n*0+k*1+m*2

所以n*0+k*1+m*2=n+m+k-1

得n=m+1

这里面的一些概念，大家又不懂的地方，可以看我的上一篇博客“数据结构：树与二叉树（一）”，下面是链接：

https://blog.csdn.net/Viadimir/article/details/105923124

（4）满二叉树（full binary tree）：高度为k的二叉树，若具有2^k-1个结点，则称之为满二叉树。说通俗点就是每个分支结点的度都是2，就是都有两个孩子结点。下面这棵树就是满二叉树：

对二叉树的结点逐层从上到下、每层从左到右进行编号，于是每个结点都有一个符号。接下来要常用到这个符号。

（5）完全二叉树（complete binary tree）：假设二叉树有n个结点，对二叉树的结点进行编号，若二叉树各结点与深度相同的满二叉树中编号相同的1~n个各结点一一对应，则称为完全二叉树。

对于完全二叉树，另外一种说法就是，若设二叉树的深度为k，那么去掉第k层，前k-1层必然构成一个满二叉树，不满的最后一层，结点首先出现在左边。

完全二叉树举例：

完全二叉树性质1：具有n个结点的完全二叉树深度为log以2为底(n+1)的对数，或者是log以2为底n的对数+1。

完全二叉树性质2：如果对一棵具有n个结点的完全二叉树的结点进行编号，则对任一结点i(1<=i<=n)有：

①若i=1，则该结点是二叉树的根，无双亲，否则，其双亲结点的编号为i/2或（i-1)/2；

②如果2*i>n，则结点i没有左孩子，否则，其左孩子的编号为2*i；

③如果2*i+1>n，则结点i没有右孩子，否则，其右孩子编号为2*i+1；

④若i为奇数，且i≠1，那么该结点必然有左兄弟，其左兄弟编号为i-1，不一定有右兄弟；；若i为偶数且i≠n，那么该结点必有右兄弟，其右兄弟编号为i+1，不一定有左兄弟。

 

3.二叉树顺序存储结构

（1）存储方式：用地址连续的空间单元来存储二叉树的各个元素，单位了表示关系，利用二叉树的性质，元素存放时，首先确定一个序号，该序号是对二叉树按完全二叉树形式编号而得，编号为i的存放在第i个位置。这种存储方式的特点是，存储位置体现层次关系，双亲i/2或(i-1)/2，孩子是2*i或者2*i+1，但是，插入、删除有可能需要移动大量元素，空间效率低。

（2）顺序存储结构举例：

也有一种极端情况，空间存储效率极低：

这种树，可以叫做完全右叉树，存储空间利用率极低。

（3）高级语言实现

#define maxdepth 二叉树的最大深度 
#define maxlen  2maxdepth-1   //maxlen连续空间的最大值 
typedef   用户数据类型 ElemType;      //定义数据元素类型 
struct sqbitree {     
    ElemType elem[1..maxlen];     //连续存储空间 
    nd:0..maxlen           //二叉树占用空间大小 
}

 

4.二叉树链式存储结构

（1）存储方式：用任意的空间单元来存储二叉树的各个元素，在存储元素时，同时也存储其相关元素的地址（左、右孩子、双亲）。

①二叉链式

②三叉链式

（2）链式存储结构特点：

①占用空间不随树的形态而变化；

②n个结点的二叉树，占用空间为：n*(存储一个元素的空间+存储指针的空间)；

③对求孩子或双亲操作容易；

④插入、删除不需要移动元素，但需要调整大量的指针；

⑤空指针比较多（有2*n-(n-1)=n+1个）。

（3）二叉树基于链式存储下的遍历操作

这个操作是二叉树中最重要的操作之一，有深度优先遍历和广度优先遍历两种方式，深度优先遍历又分为前序遍历、中序遍历、后序遍历，广度优先遍历又被称为层次遍历，具体的内容，大家可访问下面这篇博客，写的通俗易懂，很适合初学者：

https://blog.csdn.net/qq_42651904/article/details/90288715

还有一种操作就是根据二叉树的前序和中序遍历序列，构造出二叉树

这里给大家讲解一个例子

①

前序遍历序列中，第一个结点必然是根结点；中序遍历的顺序是，先左子树，后根结点，然后是右子树，所以中序遍历序列中，A结点的左右，必然是A结点的左右子树，所以将HBDF分为一堆，为A的左子树，EKCG分为一堆，为A的右子树；再往下分，前序遍历的顺序是，先根结点，然后再是左子树，然后再是右子树，所以根据前序遍历序列，在A的左右两个子树中，B必然是左子树的根结点，再带入中序遍历序列中，得出H是B的左子树，DF是B的右子树。

②

H没有左右子树；在前序序列中，FD，中序序列中，DF，根据前序和中序的遍历规则可得，F是B的右儿子，D是F的左儿子。

③

最后再看A的右子树，当然，还是根据前序和中序的遍历规则，E是右子树的根结点，E没有左孩子，C是E的右子树的根结点，K和G分别是C的左右孩子。至此，该树已经画完。

 

还有一种二叉树叫做线索二叉树，我仔细看了一下，感觉作用不是很大，甚至有点多余（也可能是我孤陋寡闻了），这里就不给大家讲了，有兴趣的童鞋可以自己上网搜一下；还有一种树叫森林，森林中，重要的知识就是遍历，而森林的遍历与二叉树的遍历相差不多，这里也不给大家讲了，按照我自己的理解，森林，就是很多棵树的集合。

 

5.二叉树链式ADT操作实现

我直接贴全部代码，就不分开贴了。

#include <iostream>
#include <queue>
#include <cstdlib>
#include <string.h>
#include <algorithm>
using namespace std;

//结点类定义
class BinTreeNode{
public:
    BinTreeNode *leftChild,*rightChild;
    char data;
public:
    BinTreeNode(){leftChild=NULL;rightChild=NULL;}
    BinTreeNode ( char x, BinTreeNode *left = NULL,
                 BinTreeNode *right = NULL ):data (x),leftChild (left),rightChild(right){}               //构造函数
    ~BinTreeNode(){}//析构函数
};

class BinaryTree{
public:
    BinTreeNode *root;
public:
    BinaryTree(){root = new BinTreeNode();}
    void CreateBinTree(BinTreeNode *&root);//创建二叉树
    void PreOrder(BinTreeNode *root);//前序遍历
    void InOrder(BinTreeNode *subTree );//中序遍历
    void PostOrder(BinTreeNode *subTree );//后序遍历
    int Depth(BinTreeNode *subTree);//计算二叉树深度（高度）
    void parent(BinTreeNode *subTree,char c);//求给定元素的双亲
};
//求给定元素的双亲
void BinaryTree::parent(BinTreeNode *subTree,char c){
    if (subTree!=NULL){
        if ((subTree->leftChild!=NULL&&subTree->leftChild->data==c)||(subTree->rightChild!=NULL&&subTree->rightChild->data==c)){
            cout<<subTree->data;
        }
        parent(subTree->leftChild,c);
        parent(subTree->rightChild,c);
    }
};
//求二叉树深度
int BinaryTree::Depth(BinTreeNode *subTree){
    if (subTree==NULL) {
        return 0;//空二叉树深度为0
    }
    else{
        return 1+max(Depth(subTree->leftChild),Depth(subTree->rightChild));
    }
};

//前序遍历
void BinaryTree::PreOrder(BinTreeNode *subTree){
    if (subTree!=NULL){
        cout<<subTree->data<<" ";
        PreOrder(subTree->leftChild);
        PreOrder(subTree->rightChild);
    }
};

//中序遍历
void BinaryTree::InOrder(BinTreeNode *subTree){
    if (subTree != NULL) { //终止递归的条件
        InOrder(subTree->leftChild);
        cout<<subTree->data<<" ";
        InOrder(subTree->rightChild );
    }
};

//后序遍历
void BinaryTree::PostOrder(BinTreeNode *subTree){
    if (subTree!=NULL){ //终止递归的条件
        PostOrder(subTree->leftChild );
        PostOrder(subTree->rightChild );
        cout<<subTree->data<<" ";
    }
};

//创建二叉树
void BinaryTree::CreateBinTree(BinTreeNode *&root){
    char ch;
    cin>>ch;
    if (ch=='#'){
        root = NULL;
    }
    else{
        root = new BinTreeNode(ch);
        CreateBinTree(root->leftChild);
        CreateBinTree(root->rightChild);
    }
};

int main(){
    BinaryTree bt;
    bt.CreateBinTree(bt.root);
    //前序遍历
    cout<<"前序遍历序列：";
    bt.PreOrder(bt.root);
    cout<<endl;
    //中序遍历
    cout<<"中序遍历序列：";
    bt.InOrder(bt.root);
    cout<<endl;
    //后序遍历
    cout<<"后序遍历序列：";
    bt.PostOrder(bt.root);
    cout<<endl;
    //计算二叉树深度
    cout<<"二叉树深度为:"<<bt.Depth(bt.root)<<endl;
    //查找给定元素的双亲
    char element;
    cout<<"请输入需要查找的元素:";
    cin>>element;
    cout<<"双亲为:";
    bt.parent(bt.root,element);
    cout<<endl;
}
//测试序列：A B H # # F D # # # E # C K # # G # #
//对于该测试序列，大家直接测试粘贴到cmd里即可
//这个测试序列就是离该段代码最近的那棵树

输出结果为：