数据结构(C语言实现) - 二叉树的基本操作(建立，遍历，结点数，叶子结点数，高度，按树状打印，输出叶子结点等）

最新推荐文章于 2024-09-07 14:22:27 发布

XW-YYDS

最新推荐文章于 2024-09-07 14:22:27 发布

阅读量1.8w

点赞数 68

分类专栏：数据结构文章标签：数据结构二叉树

本文链接：https://blog.csdn.net/Vincent_Xupt/article/details/78797907

版权

数据结构专栏收录该内容

7 篇文章

订阅专栏

通常，对二叉树的操作都是利用二叉链表进行的。

二叉链表：包括三个域-数据域，左孩子，右孩子的结点结构的二叉树存储结构。

二叉链表的存储结构如下：

typedef char DataType;
 
typedef struct node		/*二叉树的存储结构*/ 
{
	DataType data;
 	struct node *Lchild;
 	struct node *Rchild;
}BiTNode,*BiTree;

二叉树的基本操作包括：建立，递归遍历，求结点数，求叶子结点数，输出叶子结点，求二叉树的高度，求结点的双亲，按树状打印等等。完整代码如下：

#include <stdio.h>
#include <stdlib.h>

typedef char DataType;
 
typedef struct node		/*二叉树的存储结构*/ 
{
	DataType data;
 	struct node *Lchild;
 	struct node *Rchild;
}BiTNode,*BiTree;

int Count1=0;	/*统计结点数目的全局变量*/

int Count2=0;	/*统计叶子结点数目的全局变量*/ 

int depth = 0;	/*记录当前求得的最大层次*/ 

BiTNode *Create_BiTree();	/*先序建立二叉树*/	

void  PreOrder(BiTree root);	/*先序遍历二叉树*/

void InOrder(BiTree root);	 /*中序遍历二叉树*/

void PostOrder(BiTree root);	 /*后序遍历二叉树*/

void PreOrder_CalNode(BiTree root);		/*统计二叉树的结点*/

void InOrder_PrintLeaf(BiTree root); 	/*输出二叉树的叶子结点*/

void PostOrder_CalLeaf(BiTree root);	/*方法1-统计叶子结点的数目*/

int CalLeaf(BiTree root);	/*方法2-统计叶子结点的数目*/

void TreeDepth(BiTree root,int h);	/*方法1-求二叉树的高度*/

int PostOrder_TreeDepth(BiTree root);	/*方法2-求二叉树的高度*/

BiTree Parent(BiTree root,BiTree current);	/*求二叉树中某个结点的双亲*/ 

void PrintTree(BiTree root,int h);		/*按树状打印二叉树*/ 
 
int main()
{
	BiTree root;
	/*-----------------二叉树的建立-----------------*/ 
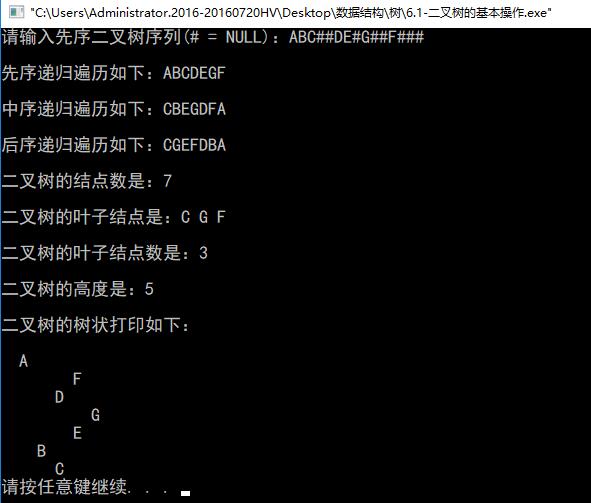
	printf("请输入先序二叉树序列(# = NULL)："); 
	root = Create_BiTree();
	
	/*-----------------二叉树的递归遍历---------------*/ 
	printf("\n先序递归遍历如下：");
	PreOrder(root);
	printf("\n\n中序递归遍历如下：");
	InOrder(root);
	printf("\n\n后序递归遍历如下：");
	PostOrder(root);
	printf("\n");
	
	/*-----------先序遍历统计二叉树中的结点数---------*/ 
	PreOrder_CalNode(root);
	printf("\n二叉树的结点数是：%d\n",Count1);
	
	/*-----------中序遍历输出二叉树的叶子结点---------*/ 
	printf("\n二叉树的叶子结点是：");
	InOrder_PrintLeaf(root);
	printf("\n");
	
	/*----------后序遍历统计二叉树的叶子结点数---------*/
	PostOrder_CalLeaf(root);
	printf("\n二叉树的叶子结点数是：%d\n",Count2); 
	
	/*----------遍历计算二叉树的高度(层次数)---------*/
	int h=1; /*h为root所在的层次,初始值为1*/
	TreeDepth(root,h);
	printf("\n二叉树的高度是：%d\n",depth);
	
	/*-----------------求某结点的双亲----------------*/
	
	
	/*-----------------按树状打印二叉树--------------*/
	h = 1;
	printf("\n二叉树的树状打印如下：\n\n");
	PrintTree(root,h);
	
	return 0;
}

BiTNode *Create_BiTree()		/*先序建立二叉树*/
{
	DataType ch;
    BiTree root;
    scanf("%c",&ch);
    if(ch=='#')		root=NULL;
    else{
        root = (BiTree)malloc(sizeof(BiTNode));
        root->data = ch;
        root->Lchild = Create_BiTree();
        root->Rchild = Create_BiTree();
    }
    return root;
}

void  PreOrder(BiTree root)	/*先序遍历二叉树*/
{
	if(root){
		printf("%c",root->data);	/*访问根节点数据*/ 
		PreOrder(root->Lchild);		/*先序访问左子树*/ 
		PreOrder(root->Rchild);		/*先序访问右子树*/ 
	}
}

void InOrder(BiTree root) /*中序遍历二叉树*/
{
	if(root){
		InOrder(root->Lchild);		/*中序访问左子树*/ 
		printf("%c",root->data);	/*访问根节点数据*/ 
		InOrder(root->Rchild);		/*中序访问右子树*/ 
	}
}

void PostOrder(BiTree root) /*中序遍历二叉树*/
{
	if(root){
		PostOrder(root->Lchild);		/*后序访问左子树*/  
		PostOrder(root->Rchild);		/*后序访问右子树*/
		printf("%c",root->data);	/*访问根节点数据*/
	}
}

void PreOrder_CalNode(BiTree root)		/*统计二叉树的结点*/
{
	if(root)
	{
		Count1++;
		PreOrder_CalNode(root->Lchild);
		PreOrder_CalNode(root->Rchild);
	}
}

void InOrder_PrintLeaf(BiTree root) 	/*输出二叉树的叶子结点*/
{
	if(root){
		InOrder_PrintLeaf(root->Lchild);
		if(root->Lchild == NULL  &&  root->Rchild == NULL){
			printf("%c ",root->data);		/*输出叶子结点*/ 
		}
		InOrder_PrintLeaf(root->Rchild);
	}
}

void PostOrder_CalLeaf(BiTree root)		/*方法1-统计叶子结点的数目*/ 
{
	if(root){
		PostOrder_CalLeaf(root->Lchild);
		PostOrder_CalLeaf(root->Rchild);
		if(root->Lchild == NULL  &&  root->Rchild == NULL){
			Count2++;		/*统计叶子结点*/ 
		}
	}
}

int CalLeaf(BiTree root)	/*方法2-统计叶子结点的数目*/
{
	int nl,nr;		/*nl,nr分别统计左右子树的叶子结点数目*/ 
	if(root==NULL) return 0;
	if(root->Lchild==NULL && root->Rchild==NULL) return 1;
	nl = CalLeaf(root->Lchild);		/*递归求左子树的叶子数*/
	nr = CalLeaf(root->Rchild); 	/*递归求右子树的叶子数*/ 
}

void TreeDepth(BiTree root,int h)	/*方法1-求二叉树的高度*/
{
	if(root){
		if(h>depth) depth = h;		/*当前结点层次大于depth,更新*/
		TreeDepth(root->Lchild,h+1);	/*遍历左子树，子树根层次为h+1*/ 
		TreeDepth(root->Rchild,h+1);	/*遍历右子树，子树根层次为h+1*/ 
	}
}

int PostOrder_TreeDepth(BiTree root)	/*方法2-求二叉树的高度*/
{
	int hl,hr,h;
	if(root==NULL) return 0;
	else {
		hl = PostOrder_TreeDepth(root->Lchild); /*递归求左子树的高度*/ 
		hr = PostOrder_TreeDepth(root->Rchild);	/*递归求右子树的高度*/
		h = (hl > hr ? hl : hr) + 1;  /*计算树的高度*/
		return h; 
	}
}

BiTree Parent(BiTree root,BiTree current)	/*求二叉树中某个结点的双亲*/
{
	BiTree p;
	if(root==NULL) return NULL;
	if(root->Lchild==current || root->Rchild==current)
	return root;						/*  *root即为current的双亲*/
	p=Parent(root->Lchild,current);		/*递归在左子树中查找*/
	if(p!=NULL) return p;
	else return(Parent(root->Rchild,current));	/*递归在右子树中查找*/ 
	
} 

void PrintTree(BiTree root,int h)		/*按树状打印二叉树*/
{
	if(root==NULL) return;
	PrintTree(root->Rchild,h+1);	/*先序打印右子树*/
	for(int i=0;i<h;i++)  printf("  ");
	printf("%c\n",root->data);		/*输出结点*/
	PrintTree(root->Lchild,h+1);	/*先序打印右子树*/ 
}

运行结果如下: