中缀表达式转换为后缀表达式

                                                           中缀表达式转换为后缀表达式

转载自http://blog.csdn.net/ssjhust123/article/details/8001651

一、后缀表达式求值

后缀表达式也叫逆波兰表达式，其求值过程可以用到栈来辅助存储。假定待求值的后缀表达式为：6  5  2  3  + 8 * + 3  +  *，则其求值过程如下：

1）遍历表达式，遇到的数字首先放入栈中，此时栈如下所示：

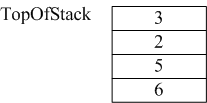
2）接着读到“+”，则弹出3和2，执行3+2，计算结果等于5，并将5压入到栈中。

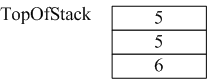
3）读到8，将其直接放入栈中。

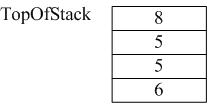
4）读到“*”，弹出8和5，执行8*5，并将结果40压入栈中。而后过程类似，读到“+”，将40和5弹出，将40+5的结果45压入栈...以此类推。最后求的值288。

 

 

二、中缀表达式转后缀表达式

2.1）规则

中缀表达式a + b*c + (d * e + f) * g，其转换成后缀表达式则为a b c * + d e * f  + g * +。

转换过程需要用到栈，具体过程如下：

1）如果遇到操作数，我们就直接将其输出。

2）如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将其放入栈中。

3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。

4）如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下我们才弹出" ( "，其他情况我们都不会弹出" ( "。也就是说这种操作，" + "的优先级最低，" ( "优先级最高。

5）如果我们读到了输入的末尾，则将栈中所有元素依次弹出。

 

2.2）实例

规则很多，还是用实例比较容易说清楚整个过程。以上面的转换为例，输入为a + b * c + (d * e + f)*g，处理过程如下：

1）首先读到a，直接输出。

2）读到“+”，将其放入到栈中。

3）读到b，直接输出。

此时栈和输出的情况如下：

 

4）读到“*”，因为栈顶元素"+"优先级比" * " 低，所以将" * "直接压入栈中。

5）读到c，直接输出。

此时栈和输出情况如下：

 

6）读到" + "，因为栈顶元素" * "的优先级比它高，所以弹出" * "并输出， 同理，栈中下一个元素" + "优先级与读到的操作符" + "一样，所以也要弹出并输出。然后再将读到的" + "压入栈中。

此时栈和输出情况如下：

 

7）下一个读到的为"("，它优先级最高，所以直接放入到栈中。

8）读到d，将其直接输出。

此时栈和输出情况如下：

 

9）读到" * "，由于只有遇到" ) "的时候左括号"("才会弹出，所以" * "直接压入栈中。

10）读到e，直接输出。

此时栈和输出情况如下：

 

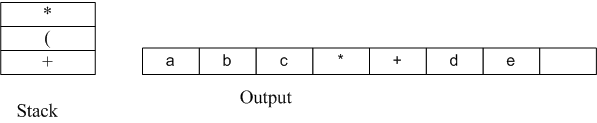
11）读到" + "，弹出" * "并输出，然后将"+"压入栈中。

12）读到f，直接输出。

此时栈和输出情况：

 

 

13）接下来读到“）”，则直接将栈中元素弹出并输出直到遇到"("为止。这里右括号前只有一个操作符"+"被弹出并输出。

 

14）读到" * "，压入栈中。读到g，直接输出。

 

15）此时输入数据已经读到末尾，栈中还有两个操作符“*”和" + "，直接弹出并输出。

至此整个转换过程完成。程序实现代码后续再补充了。

 

 2.3）转换的另一种方法

1)先按照运算符的优先级对中缀表达式加括号，变成( ( a+(b*c) ) + ( ((d*e)+f) *g ) )

2)将运算符移到括号的后面，变成((a(bc)*)+(((de)*f)+g)*)+

3)去掉括号，得到abc*+de*f+g*+