基于comsol的双目标函数流热拓扑优化液冷板结构设计，双目标函数为 大换热量 大和

基于COMSOL的双目标函数流热拓扑优化：液冷板结构设计的新思路

摘要：
本文将探讨基于COMSOL的双目标函数流热拓扑优化在液冷板结构设计中的应用。通过建立数学模型，将最大换热量和最小流体功率耗散最小作为无量纲化的双目标函数，实现流道和热结构的协同优化设计。本文将介绍优化设计的方法、实施过程及结果分析，以期为液冷板结构设计的优化提供新的思路。

一、引言

随着电子设备的日益普及和高度集成化，设备的散热问题越来越受到关注。液冷板作为一种新型的散热技术，其结构设计对于设备的散热性能具有重要影响。本文将基于COMSOL，采用双目标函数流热拓扑优化的方法，对液冷板的结构设计进行深入研究。

二、双目标函数流热拓扑优化的基本原理

双目标函数流热拓扑优化是一种基于数值模拟和优化算法的结构设计方法。该方法将最大换热量和最小流体功率耗散最小作为无量纲化的双目标函数，通过优化算法对流道和热结构进行协同优化设计。在优化过程中，COMSOL将根据设定的边界条件和物理参数，对结构进行数值模拟和分析，从而得到最优的设计方案。

三、液冷板结构设计的数学模型建立

在液冷板结构设计的数学模型建立中，我们需要考虑流道的形状、尺寸、位置以及材料的热导率等因素。通过建立数学模型，将双目标函数进行无量纲化处理，以便于进行优化计算。在模型中，我们将采用适当的边界条件和物理参数，以反映液冷板在实际工作过程中的热环境和流体流动情况。

四、优化设计的方法与实施过程

在优化设计的过程中，我们首先需要确定优化的目标和约束条件。然后，通过COMSOL进行数值模拟和分析，得到不同设计方案下的流场、温度场以及流体功率耗散等情况。接着，我们根据双目标函数的无量纲化处理结果，对设计方案进行评估和比较，最终得到最优的设计方案。

五、结果分析

通过双目标函数流热拓扑优化的方法，我们可以得到液冷板结构设计的最优方案。与传统的设计方法相比，该方法可以更好地考虑流道和热结构的协同优化设计，从而提高设备的散热性能。同时，通过无量纲化的双目标函数处理，我们可以更加客观地评估不同设计方案的性能，为设计人员提供更加准确的决策依据。

六、代码实现与案例分析

以下是基于COMSOL的液冷板结构设计的代码实现示例：

% 导入COMSOL相关模块
% ... 省略导入代码 ...

% 建立数学模型并设定边界条件和物理参数
% ... 省略建模代码 ...

% 进行数值模拟和分析，得到不同设计方案下的流场、温度场以及流体功率耗散等情况
% ... 省略模拟和分析代码 ...

% 根据双目标函数的无量纲化处理结果，对设计方案进行评估和比较
% ... 省略评估和比较代码 ...

% 输出最优设计方案的相关数据和图形结果
% ... 省略输出代码 ...

通过以上代码实现，我们可以得到液冷板结构设计的最优方案，并对不同设计方案进行评估和比较。下面是一个案例分析的例子：

在某电子设备中，采用液冷板进行散热。通过双目标函数流热拓扑优化的方法，我们得到了最优的液冷板结构设计方案。与传统的设计方法相比，该方案在保证最大换热量的同时，将流体功率耗散降到了最低，从而提高了设备的散热性能。经过实际应用测试，该设计方案在保证设备正常运行的同时，有效地降低了设备的温度，提高了设备的稳定性和可靠性。

七、总结与展望

本文介绍了基于COMSOL的双目标函数流热拓扑优化在液冷板结构设计中的应用。通过建立数学模型和优化算法，实现了流道和热结构的协同优化设计。该方法可以更好地考虑设备的实际工作情况和需求，从而提高设备的散热性能。未来，我们将继续深入研究双目标函数流热拓扑优化的方法，探索更加高效和可靠的液冷板结构设计方案，为电子设备的散热技术提供新的思路和方法。
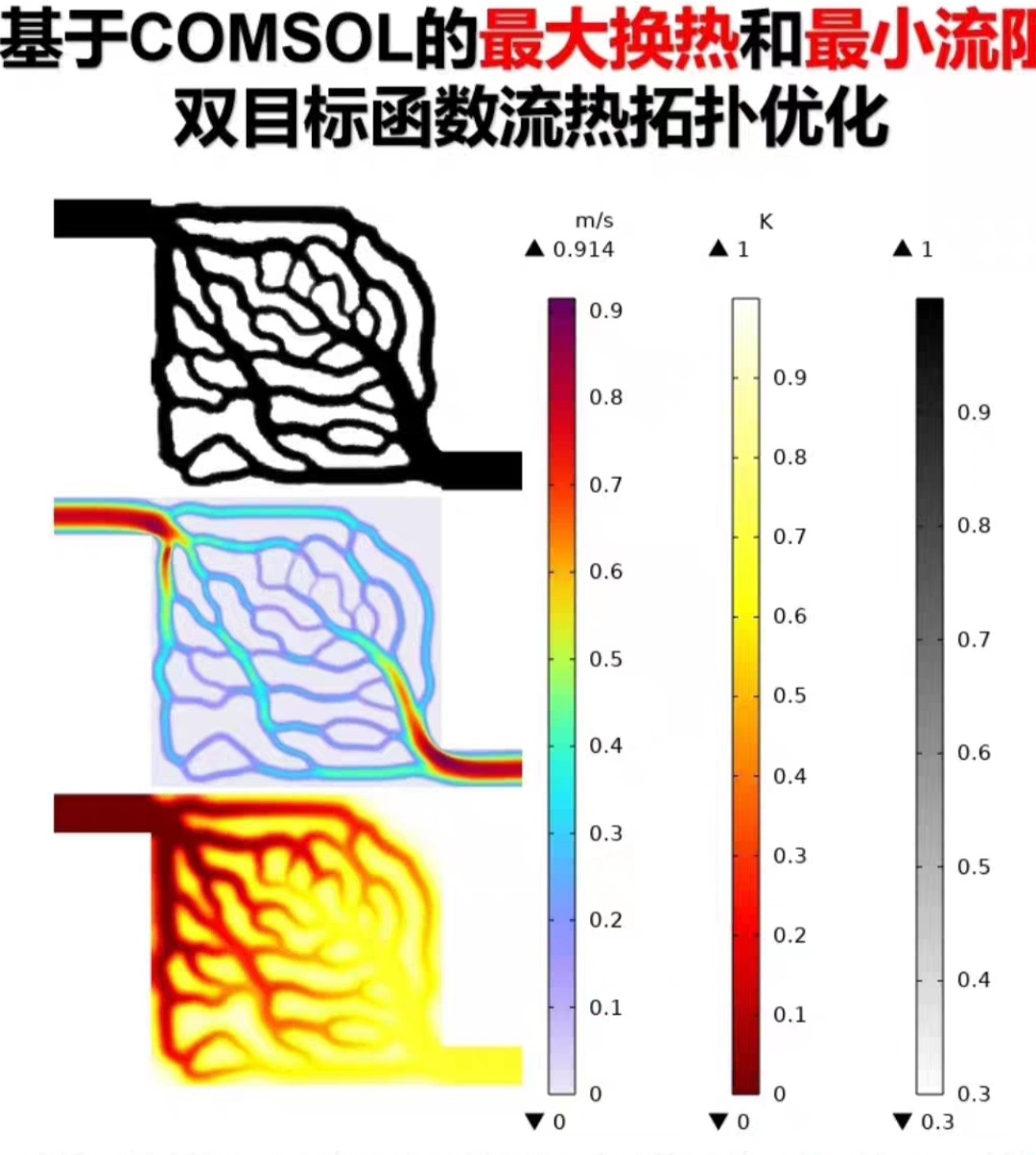
基于comsol的双目标函数流热拓扑优化液冷板结构设计，双目标函数为最大换热量最大和最小流体功率耗散最小的无量纲化