数据结构之二叉查找树介绍

目录

一、定义

二、二叉查找树的搜索

三、二叉查找树的插入

四、二叉查找树的删除

五、总结

---

一、定义

二叉查找树（Binary Search Tree），也叫二叉搜索树或二叉排序树，它或者是一棵空树。

二叉查找树具有下列性质：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树；

下图就是一个标准的二叉查找树：

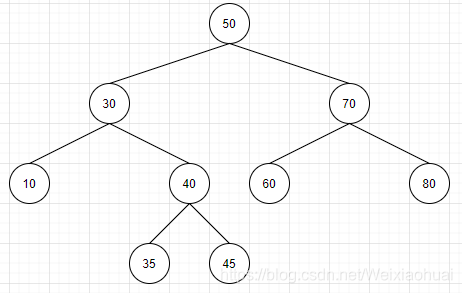
可见，从根节点50开始，左子树的所有节点的值都比根节点50小，右子树的所有节点的值都比根节点大。

二、二叉查找树的搜索

根据上面提到的二叉查找树的特性，当搜索一个节点在树中的位置时，我们需要从根节点出发：

• （1）如果查找的元素对应的值比当前节点对应的值小，则到它的左子树去进行查找；
• （2）如果查找的元素对应的值比当前节点对应的值大，则到它的右子树去进行查找；
• （3）如果查找的元素对应的值等于当前节点对应的值，说明找到了；
• （4）如果直至叶子节点都找不到对应的值，说明该元素不存在该树中；

以上面的二叉查找树为例，如果我们要搜索45节点在树中的位置，大体流程如下：

• 【a】从根节点50出发，45 < 50，小于50，则去50的左子树进行查找，当前节点变为30；
• 【b】比较45 > 30，大于30，则去30的右子树进行查找，当前节点变为40；
• 【c】比较45 > 40，大于40，则会40的右子树进行查找，当前节点变为45；
• 【d】比较45 = 45，刚好相等，找到目标节点，整个查找过程结束；

如下图所示：

三、二叉查找树的插入

二叉查找树进行插入的话，首先必须找出需要插入的位置，这个搜索过程跟上面的流程一样，找到插入位置后直接插入即可，大体包括下面的步骤：

• 如果当前二叉查找树是一颗空树，则直接创建节点进行插入即可；
• 如果当前二叉查找树不是空树，则有下面三个情况：
• 如果插入节点的值比当前节点的值小，则到它的左子树去插入，依次递归查找，如果左子树或者节点为空，则插入到这个位置；
• 如果插入节点的值比当前节点的值大，则到它的右子树去插入，依次递归查找，如果右子树或者节点为空，则插入到这个位置；
• 如果插入节点的值与当前节点的值相等，说明该元素已经在树中存在了，直接返回；

下面以一个示例说明二叉查找树的插入过程：依次插入元素【10、21、30、15、25、35、40、5】，下面是具体的构建过程：

总体原则：根据左小右大找到插入位置进行插入。

【a】插入10

【b】插入20

【c】插入30

【d】插入15

【e】插入25

【f】插入35

【g】插入40

【h】插入5

可见，构建过程比较简单，就是挨个进行比较，比当前节点值小就去左子树去插入，比当前节点值大就去右子树去插入。

四、二叉查找树的删除

删除节点也会涉及到查找删除的节点位置这一步，同样跟上面的查找流程类似。删除前首先要找到该节点，如果找不到，说明树中不存在此节点，不进行任何操作，直接结束即可。

 二叉查找树删除大致可以分为以下三种情况：

• 删除节点是叶子节点，无子节点，直接删除即可；
• 待删除的节点只有一个子节点，那么用该子节点接到删除节点的父节点即可；
• 待删除的节点有两个子节点，那么使用前或后继节点作为替换节点，对删除节点进行数据替换，然后转移至删除替换节点即可；

【a】删除节点是叶子节点，无子节点

 如果删除节点35，因为35是叶子节点，所以直接删除即可。

【b】待删除的节点只有一个子节点，那么用该子节点接到删除节点的父节点即可

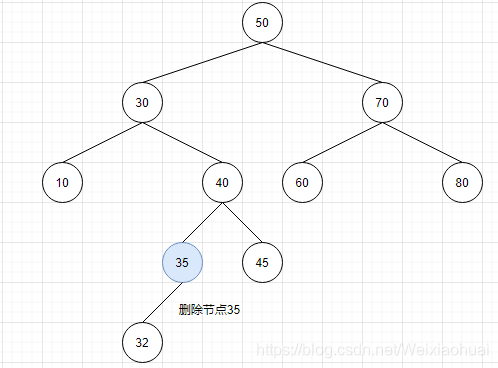
如果我们删除节点35，因为35只有一个子节点32，所以只需要将32连接到40的左子树上面，断开35和40的连接即可，如下图：

【c】待删除的节点有两个子节点，那么使用前或后继节点作为替换节点，对删除节点进行数据替换，然后转移至删除替换节点即可

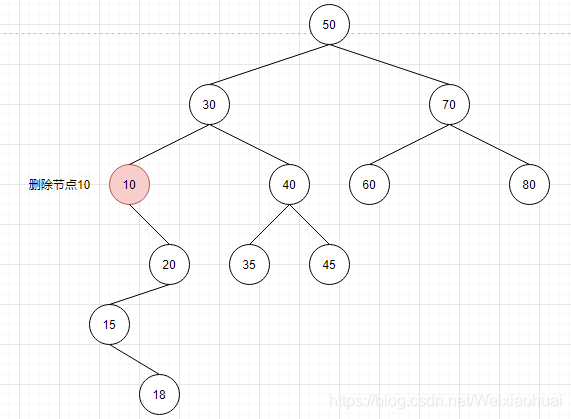
在二叉搜索树中，寻找前后继节点很简单：

• 前继节点：小于当前节点的，在左子树中最右边的那个节点。
• 后继节点：大于当前节点的，在右子树中最左边的那个节点。

查找过程：

• （1）寻找前继节点，当前节点左子树进行查找，然后右转一直走到底（右子节点为null时终止）；
• （2）寻找后继节点，当前节点右子树中查找，然后左转一直走到底（左子节点为null时终止）；

如下图所示：

下面我们需要删除节点10，具体删除流程如下图所示：

注意：上图中的15应该是10的后继节点，笔者笔误了。

五、总结

本文主要总结了二叉搜索树的一些特性，以及二叉搜索树的查找流程、插入、删除流程，并通过示例讲解了具体是怎么操作的，但是二叉搜索树在极端情况下的查询效率不是很高，复杂度可能会是O(n)，如下图：

 

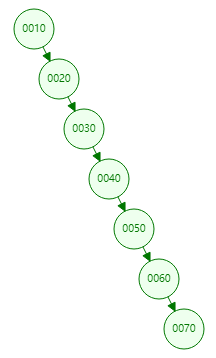
造成上面的原因主要是树不平衡，为了解决这种不平衡，推出了平衡二叉搜索树，平衡二叉搜索树（AVL树、红黑树等）就是为了解决这个问题：

平衡二叉树在进行插入、删除后，会进行自平衡，从而保证其查询的时间复杂度接近于O(log2n)。

小伙伴们可以在下面的网址进行动态构建二叉搜索树、红黑树等等，可以加深二叉搜索树的插入、删除等流程。

https://www.cs.usfca.edu/~galles/visualization/BST.html