原文:https://blog.csdn.net/henucm/article/details/98492753
题意:给你x0、x1 a、b、mod,根据 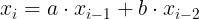 求出
求出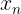

根据上述公式,再套用十进制矩阵快速幂即可(二进制好像会超时...)
用十进制
设 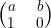 为res 则可得
为res 则可得 ![\large ans=res^{n[i]-'0'}](https://i-blog.csdnimg.cn/blog_migrate/e823febf68b7be4093e36a99113f014c.gif)
我们再设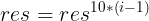
就是分解n为每一位,再去相乘。
例如 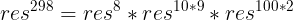
讲计算出来的![\large res.m[1][0]*x1+res.m[1][1]*x0](https://i-blog.csdnimg.cn/blog_migrate/ec6ce18900aebc72b471138e2c6fca82.gif) 即可
即可
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
//typedef __int128 bll;
const ll maxn = 1e6+100;
//const ll mod = 1e9+7;
const ld pi = acos(-1.0);
const ll inf = 1e18;
const ld eps = 1e-5;
const ld e = exp(1);
ll x0,x1,a,b,mod;
char str[maxn];
struct mat
{
ll m[2][2];
};
mat mul(mat a,mat b)
{
mat res;
for(int i = 0; i < 2; i++)
for(int j = 0; j < 2; j++)
res.m[i][j] = 0;
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
for(int k = 0; k < 2; k++)
{
res.m[i][j] = (res.m[i][j]%mod + a.m[i][k]*b.m[k][j]%mod )%mod;
}
}
}
return res;
}
mat qpow(mat a,int b)
{
mat e;
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
i == j? e.m[i][j] = 1 : e.m[i][j] = 0;
}
}
while(b)
{
if(b&1)
e = mul(e,a);
a = mul(a,a);
b = b >> 1;
}
return e;
}
mat qpow10()
{
mat x,e;
x.m[0][0] = a; x.m[0][1] = b;
x.m[1][0] = 1; x.m[1][1] = 0;
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
i == j? e.m[i][j] = 1 : e.m[i][j] = 0;
}
}
int len = strlen(str+1);
for(int i = len; i >= 1; i--)
{
int tmp = str[i]-'0';
if(tmp > 0)
{
mat t = qpow(x,tmp);
e = mul(e,t);
}
x = qpow(x,10);
}
return e;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin >> x0 >> x1 >> a >> b >> str+1 >> mod;
mat res = qpow10();
//cout << (res.m[0][0]%mod) << endl;
cout << ( (res.m[1][0]*x1%mod)+(res.m[1][1]*x0%mod) )%mod << endl;
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








