样本收集问题

转自:http://blog.csdn.net/zhizichina/article/details/7024015

机器人Rob在一个有n*n 个方格的方形区域F 中收集样本。（i,j）方格中样本的价值为v(i,j)，如下图所示 

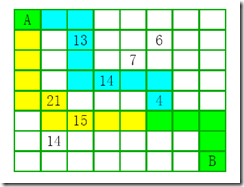
Rob 从方形区域F 的左上角A点出发，向下或向右行走，直到右下角的B 点，在走过的路上，收集方格中的样本。Rob 从A点到B 点共走2次，试找出Rob 的2条行走路径，使其取得的样本总价值最大。给定方形区域F 中的样本分布，编程计算Rob 的2条行走路径，使其取得的样本总价值最大。由文件input.txt给出输入数据。第1 行有1 个正整数n，表示方形区域F有n*n 个方格。接下来每行有3 个整数，前2 个表示方格位置，第3个数为该位置样本价值。最后一行是3个0。

 

由于机器人只能往右走或向下走，所以如果每个位置走过后，它左边或上边的点就不需要考虑了。每个机器人到达终点时都经过2*n-2步。可以设h[x1][y1][x2][y2] 表示第一个机器人到达(x1,y1)第二个机器人走到(x2,y2)时的最优值。如果现在为第S步，如果某个机器的X坐标被确定，那么它的Y坐标也可以推出来（有X+Y = S)。于是我们可以有在第由第S步的最大值去更新S+1步的最大值即可。

 

而在S步时，可以根据所在的两个位置选择一个方向进行推导（共四个，每个机器人往下或往右）。更新时需要注意如果两个机器人走到同一个格子时，它的值只更新一次（每个样本只能收集一次）。

 

现在只剩下一个难点：为什么这样递推是正确的？ 
我们使用的是第S步推导第S+1步，我们知道在第S步时，它左边，上边的方格我们己经不会再使用了，而S+1步所更新的值的位置在它的右边与下边，这样我们就保证了更新的时候没有哪一次把某个方格的值取了两次（如果两个机器人走向同一个方格，需要特殊判断）。这样就保证了算法的正确性。

 

#include <iostream>
#include <cstdio>
using namespace std;

#define MAXN 22

int h[MAXN][MAXN][MAXN][MAXN];
int v[MAXN][MAXN];
int n;

void update(int x1, int y1, int x2, int y2, int val) {
if(y1 >= n || y2 >= n)
return;
if(x1 >= n || x2 >= n)
return;
if(x1 == x2 && y1 == y2) {
h[x1][y1][x2][y2] = max(h[x1][y1][x2][y2], val + v[x1][y1]);
} else {
h[x1][y1][x2][y2] = max(h[x1][y1][x2][y2], val + v[x1][y1] + v[x2][y2]);
}
}


int main() {
scanf("%d", &n);
memset(v, 0, sizeof(v));
int x, y, val;
while(scanf("%d %d %d", &x, &y, &val) && x != 0) {
v[x - 1][y - 1] = val;
}
memset(h, 0, sizeof(h));
h[0][0][0][0] = v[0][0];

/*

此题最重要的思路是以机器人总共走多少步为对象，由x坐标来确定y坐标

*/
for(int s = 0; s < 2 * n - 2; ++s) {
for(int x1 = 0; x1 < n && x1 <= s; ++x1) {
for(int x2 = 0; x2 < n && x2 <= s; ++x2) {
int y1 = s - x1;
int y2 = s - x2;
int v = h[x1][y1][x2][y2];

//此处省略了下面注释掉的四条语句,因为如果确定了d[x1+1][y1][x2+1][y2]，d[x1+1][y1][x2][y2]的值就不需要了

/*

update(x1+1,y1,x2,y2);

update(x1,y1+1,x2,y2);

update(x1,y1,x2+1,y2);

update(x1,y1,x2,y2+1);

*/
update(x1 + 1, y1, x2 + 1, y2, v);
update(x1 + 1, y1, x2, y2 + 1, v);
update(x1, y1 + 1, x2 + 1, y2, v);
update(x1, y1 + 1, x2, y2 + 1, v);
}
}
}
printf("%d/n", h[n - 1][n - 1][n - 1][n - 1]);
return 0;
}