

什么是紧凑频率估计器呢?它是概率数据结构(英文是Probabilistic Data Structures,简称PDS)的一种。
而PDS又是什么呢?它是一类工具,用来紧凑地表示大量数据,然后只使用这种小巧紧凑的数据表示来回答有关数据的查询,提供近似的答案。它牺牲了一定的准确性,但能换取存储空间和计算速度的优化。


PDS主要有三类,一种是频率估计PDS,它帮助高效地统计大数据流中某个元素出现的次数,如网络流量分析、关键词统计等,主要代表为Count-Min Sketch和HeavyKeeper;
一种是成员查询PDS,它帮助快速回答元素是否在集合中的问题,如在网络安全中用来快速判断是否接触过恶意网址或IP地址,在大数据处理时判断某个数据是否已处理等,主要代表为我们上面所说的Bloom filter和Cuckoo filter;
还有一种是基数估计PDS,它用于估算大数据集合中不同元素的数量,如网站不同访问用户数统计等,主要代表为HyperLogLog和KMV。
其中,这个频率估计PDS就是所谓的紧凑频率估计器。

本文主要探讨的是对抗环境中的紧凑频率估计器,我们为什么需要它呢?正如前面所说,紧凑频率估计器可以高效地统计大数据流中某个元素出现的次数,因此我们可以用它们找出网站上访问量最大的网页,或者识别可能的拒绝服务威胁。

现在,关于紧凑频率估计器的性能如何,文章有一些特定的设置和探讨。
可以看到,右侧有一个数据流,正常情况下它独立于左边的紧凑频率估计器的内部结构,因为有独立性,因此紧凑频率估计器在实验中会表现得很好。

独立性:意味着数据流是随机的,不会被CFE内部的规则或设置影响。数据不会“故意”去触发CFE的弱点,CFE可以按设计正常工作。
表现好:因为没有“针对性”问题,CFE不会被特殊的数据流欺骗或干扰,所以能正常发挥出它应有的效果和准确性。
打个比方,假设CFE是一个过安检的机器,如果人流是随机的,这台机器就能稳定识别每个人。但如果人群是根据机器的弱点“设计”过的,比如有些人知道它识别不了某种特定的东西,那这台机器的表现就会很差。

但是,如果这一点没有得到满足,也就是在数据流和CFE之间没有这种独立性了,那么这些频率估计器在这种特定情况下会不会表现失常?

例如,我们先向频率估计器查询某些信息,然后得到某些答案。在这种情况下,数据流和CFE是分开的,CFE会正常运行,并给出答案。

之后,我们将根据之前得到的答案来决定数据流的后续部分(f(ans), g(ans)),也就是说,数据流“依赖”于CFE的答案,这种依赖关系就像是数据流在“观察” CFE 的表现,并根据它的回答来进行调整。

在这种依赖关系下,CFE会不会出现“异常表现”?也就是说,如果数据流根据 CFE的回答来调整内容,CFE是否还能像之前那样准确地估计频率?这就好比一个人根据某个规则去应对一个机器测试,如果这个人知道机器的工作原理并做出相应调整,那么机器可能会被“欺骗”或误导。

答案是肯定的,作者发现了某些攻击,它们可以使得某些元素的频率被严重高估或低估。

这篇论文的主要关注点由此诞生。
一是对抗者如何干扰两个紧凑型频率估计器--count-min sketch(简称CMS)和heavy Keeper(简称HK)--的功能?
二是我们能否减少CFE的估计误差,并使它们在对抗性环境中也具有鲁棒性?

对于第一部分,我们主要讨论这个Count-min sketch。
Count-min sketch,简称CMS,很容易解释。可以说,它是一个由K * m个计数器组成的矩阵。初始化时,我们将所有计数器都设置为0。

然后当我们想在CMS中插入一个元素X时,该元素会首先被K个独立的哈希函数处理。一个哈希函数与CMS的一行相关联。
第一个哈希函数处理后得到的值是5,于是我们找到CMS第一行的第5个位置;第二个哈希函数处理后得到的值是9,于是我们找到CMS第二行的第9个位置;第三个哈希函数处理后得到的值是3,于是我们找到CMS第三行的第3个位置。

然后,我们递增这些位置处的计数器,此元素插入就到此结束。

当我们想要知道某个元素的出现频率时,我们查询CMS并获得频率估计值。

此时,被查询的元素会再次被同样的K个独立的哈希函数处理,这样我们可以获得与元素相关的计数器。

然后,我们取这些计数器的最小值。

在我们的例子中,最小值为39,这就是我们需要的频率估计值。至于为什么是最小值呢?因为计数器是共享的,其他元素在插入的时候也可能会使得我们查询的元素的计数器的值增大,因此它们会高估元素的频率。而最小值相对来说是最接近真实值的,因为它受其他元素影响最小,能更准确反映目标元素的实际频率。

然而,CMS的哈希函数H1H2和H3基本上都是使用可公开计算的哈希函数实现的。

因此,攻击者不仅可以在CMS中插入任意元素,操控计数器;也可以查询频率估计值,获取结果;还可以直接访问底层哈希函数,了解它们是如何工作的,从而进行有针对性的操作。

而攻击者的目标是,在他们获得的特定目标元素输入上,他们需要将误差最大化。对于CMS,就是使得查询所得的元素频率远远高于实际的元素频率。

接下来我们来看看具体的CMS攻击流程。

对于我们的CMS来说,攻击的大纲如下:对抗者首先要找到一个集合,我们称之为目标的覆盖集合cover set。举例来说,如果a和x在第一行共用一个计数器,b和x在第二行共用一个计数器,c和x在第三行共用一个计数器,那么{a,b,c}就是一个覆盖集合。

找到覆盖物后,我们将其重复插入到CMS中,不断累积误差。通过这种攻击,我们得到的误差大约是插入次数除以k,其中k是CMS中的行数。

为了让大家更直观的了解这样做的误差,我们假设插入次数为2的20次。这样,我们的误差约为350k。这是个非常大的误差,不在合理误差范围内。


总的来说,现在让我们试着弄清楚我们的攻击实际上导致了什么。
在CMS中,我们看到我们可以将数据流中本来没有的元素标记为非常频繁出现,或者使得高频率出现的元素标记为从未出现。
因此,我们遗憾地发现,现有的紧凑频率估计器并不具有对抗性鲁棒性。

然而,本文作者的研究并没有就此止步。既然有一系列的频率估计器,而对它们进行分析,其中有些估计器只会高估,有些只会低估。例如,CMS只能高估,而Heavy-keeper只能低估。那么,如果我们将两者结合起来会发生什么呢?
这里我们补充说明一下为什么HeavyKeeper只能低估。是因为它在设计上会“遗忘”一些不常见的元素,只保留更频繁出现的元素的记录。打个比方,HeavyKeeper 就像是一张有限的排行榜,它只能容纳有限数量的选手(数据)。如果有新选手进来但积分不够高,系统会自动“忽略”他们,让他们在排行榜上没有位置。
这种机制会导致低估:因为一旦某个元素不够“热门”,它就可能被踢出或不被记录,导致系统对它的出现次数估计比实际的要低。但对于频繁出现的元素,HeavyKeeper会比较准确地记录,所以它不会高估这些热门元素的频率。这就是为什么HeavyKeeper在设计上只能低估数据,而不会高估的原因。

本文作者做到了将两者结合这一点。现在,首先进行CMS估计,然后进行HK估计。对它们进行细化后,以一种方式将它们结合在一起,并尝试从这两种结构的相互作用中获得最大的收益,然后我们可以得到最终的频率估计值。

作者将这一新成果称为Count Keeper即CK。

而对于这个新计数器CK,它的最大误差是CMS和HK估计值之差的1/2。

在作者的诚实设置实验,也就是无对抗者攻击时的实验中,CK与CMS和HK一样表现出色。

接下来,对于对抗环境中的实验,我们的攻击与对CMS的攻击类似。
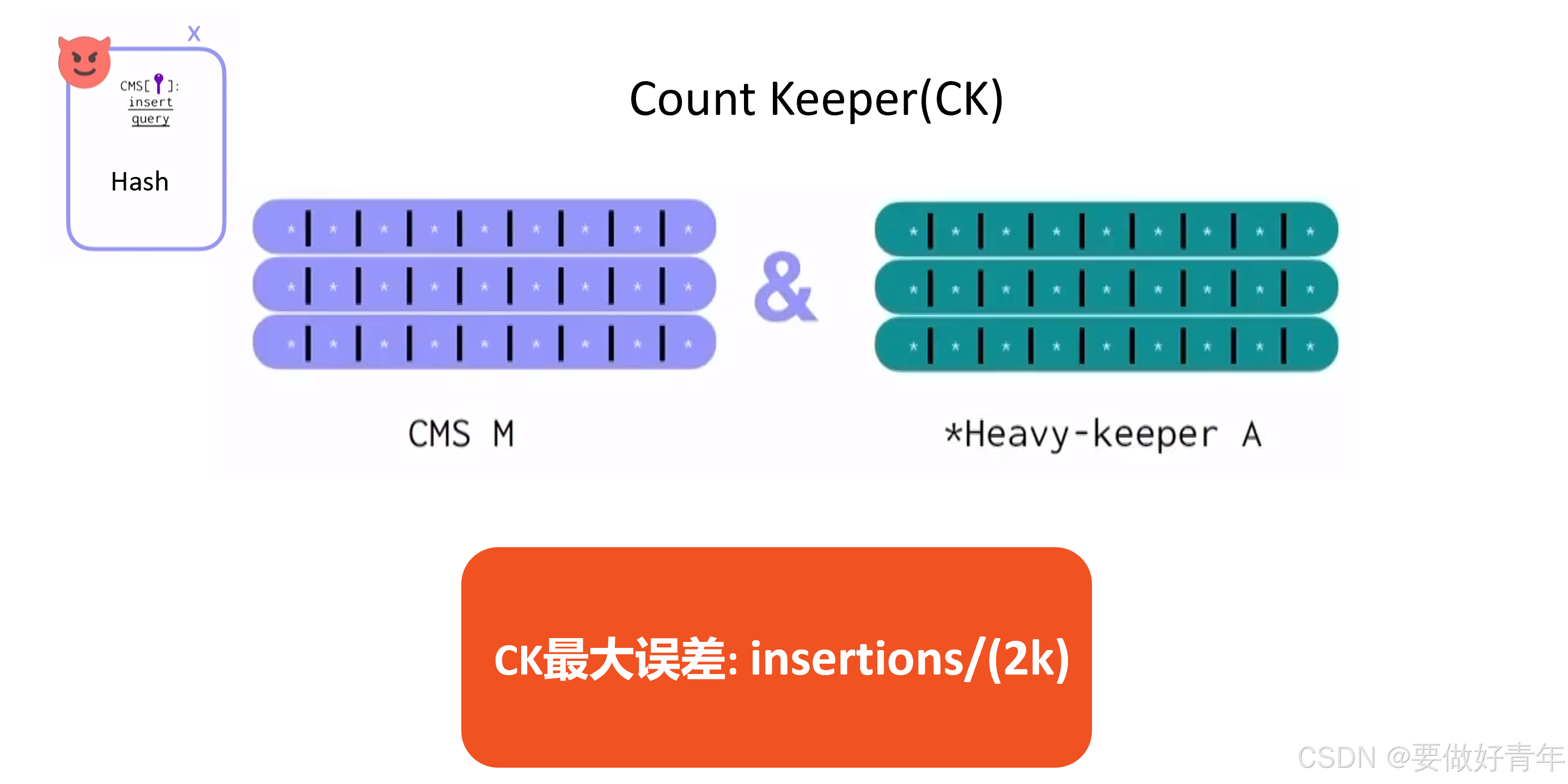
但得到的CK的最大误差是CMS误差的1/2。即插入次数除以2k,其中k是计数器的行数。

总的来说,通过运行攻击实验证实了CK确实具有更强的鲁棒性,它的最大误差是CMS的1/2,并且远小于HK误差的1/2。

但这并不是文章作者所做的全部工作,在此之外,他们提出的CK还可以检测到可疑的估计值。

它能够根据CMS与HK估计值之间的差异来举旗,从而对可疑的元素估计值进行标记。这是我们在CMS或HK中看不到的。
实施了这一策略后,在对抗性设置中,会发现每个目标元素都会被标记,说明目标元素遭受到了攻击;而在正常设置实验中,标记率非常低。这样的机制可以让紧凑频率估计器在对抗性环境中更加稳健。

本文作者目前的工作就是这些,但是进一步地,他们也在想,如果把不同的高估和低估计数器结合在一起会怎样?能否获得更好的对抗鲁棒性?

此外,能否利用某种低成本的加密技术,创造出具有数据很难被对抗者攻击的紧凑频率计数器?
这些都是开放性问题以及他们想在未来完成的工作。

最后,我们来总结一下这篇文章…

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








