前置知识:
lowbit()函数:
取出一个数二进制形式下的最低位的1及其后面的0
例如:lowbit(40)=lowbit(101000)=1000=8
具体实现方式:
inline int lowbit(int x){
return x&(-x);
}40 = 0101000
-40 = 1011000
(40) & (-40) = 1000 = 8
其实可以略微理解一下,因为负数在计算机里面是用补码存储,取反加一,正好就是把最后一个1和后面的0保留,前面的所有位都取反了。
树状数组结构:
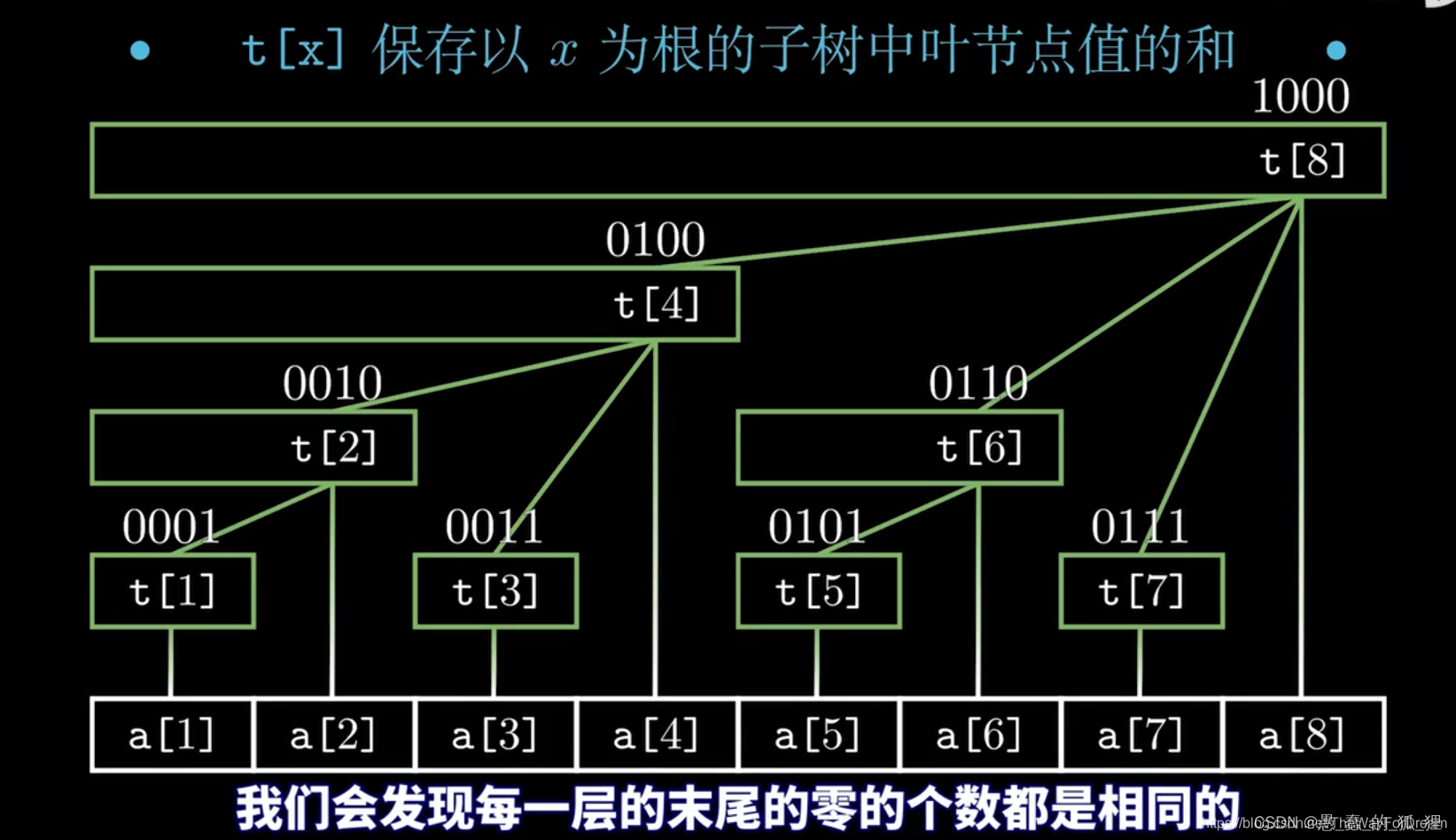
可以看到,数组下标与其所包含的和的对应关系是:t[i]包含 i-lowbit(i)+1 ~ i 的全部和。
可以从二进制的角度理解一下,这种方案可以表示所有1-i的区间,因为把i转化为二进制后可以一段一段的把最后的一个1消除掉。
例如需要表示a[1]~a[7]的和:
t[7] = t[0111] = a[7] // 7-lowbit(7)+1 = 7
t[6] = t[0110] = a[5] + a[6] // 6-lowbit(6)+1 = 5
t[4] = t[0100] = a[1] + a[2] + a[3] + a[4] // 4-lowbit(4)+1 = 1
a[1]~a[7]的和 = t[4] + t[6] + t[7]
t[7]在这里负责涵盖最后一个1的计值范围,也就是111~111和。
t[6]在这里负责涵盖101~110的和,也就是倒数第二个1的范围。
t[4]在这里负责涵盖001~100的和,也就是倒数第三个1的范围。
每一段都是负责把最后一个1消除掉的范围。这样就可以表示所有1~i的区间。
所以只要理解了这个原理,就能知道为什么要lowbit函数了。
一维树状数组:
单点修改、区间查询:
树状数组为t[i],维护a[i]的和
单点修改:
要实现单点修改,从本质上我们可以理解为:当需要修改a[i]的值的时候,我们要把所有包含a[i]的t[i]都修改一遍。
在前置知识树状数组结构中我们理解了t数组的包含关系,那么我们更新的算法就能轻易的写出来:
//a[index]+e
void add(int index,int e){
a[i] += e;
for(int i=index; i<=n; i+=lowbit(i))
t[i] += e;
}还是拿一个例子来说明,假设我要把a[3]+5:
t数组的更新顺序如下:
t[3] = t[0011] += 5 // t[3] = a[3]
t[4] = t[0100] += 5 // 3+lowbit(3)=4 t[4] = a[1] + a[2] + a[3] + a[4]
t[8] = t[1000] += 5 // 4+lowbit(4)=8 t[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8]
在所有的t中,只有这三个元素是包含了a[3]的,其他都不包含。
对于t[i]而言,包含他且离他最近的元素一定是t[i+lowbit(i)],且不存在一个t[k]只包含t[i]的一部分。
区间查询:
树状数组只能直接查找1-i这种形式的区间和,但是可以在这个基础上进行修改:
比如我需要j~i这个区间的和,我可以先查询sum(1 ~ j-1),再查询sum(1 ~ i),然后用sum(1 ~ i) - sum(1 ~ j-1),得出的结果就是j~i区间的和了。
可以写出求和代码:
//求a[1]~a[index]的和
int sum(int index){
int ans = 0;
for(int i=index; i; i-=lowbit(i))
ans += t[i];
return ans;
}求和原理可以看前置知识:树状数组结构。
区间修改、单点查询:
区间修改:
如果需要用树状数组实现区间修改,我们需要引入差分的概念:
d[i] 是差分数组,对应a[i] 有如下关系:
d[i] = a[i] - a[i-1]
d[i] 的用处是实现以下关系:
例如:
a[1~8] = {1,2,3,4,5,6,7,8}
d[1~8] = {1,1,1,1,1,1,1,1}
可以很快的发现这个关系: 是成立的
这时候我们如果把d[3] + 1
d[1~8] = {1,1,2,1,1,1,1,1}
再用 这个公式去计算a[i]可以得出:
a[1~8] = {1,2,4,5,6,7,8,9}
我们会惊喜的发现:a[3~8]都被加1了,这就是差分数组的作用,可以把一段区间同时变化,但只用修改一次。
但是如果我不想把a[3~8]都加1怎么办呢?我只想把a[3-5]加1。
我们只要把a[6-8]再加上-1不就可以了吗?
根据之前的原理:我们只要把d[6] - 1就可以实现了!
d[1~8] = {1,1,2,1,1,0,1,1}
推出a:
a[1~8] = {1,2,4,5,6,6,7,8}
至此,我们已经明白了差分的原理:
这与我们之前:单点修改、区间查询 的功能不是不谋而合吗?
我们只要维护d数组的前缀和(前缀和就是指d[1] + d[2] + ... + d[i])就能得到a[i],而且,如果我们想要修改某一段a[i~j] 只要维护d数组中的两个点就可以了(d[i] 和 d[j+1])。
我们可以给出区间修改的算法:
void add(int index,int e){
for(int i=index; i<=n; i+=lowbit(i))
d[i] += e;
}
//a[i~j] + e
void change(int i,int j,int e){
add(i,e);
add(j+1,-e);
}这样维护d数组后就可以实现d的前缀和就是a的值。
单点查询:
根据之前的理解,单点查询
算法如下:
//查询a[index]的值
int find(int index){
int ans = 0;
for(int i=index; i;i-=lowbit(i))
ans += d[i];
return ans;
}区间修改,区间查询:
区间修改:
因为需要实现区间查询,那么之前的区间修改方案肯定就不适用了,我们只能利用差分的思想,另辟蹊径:
接下来是一串数学推导:
在 区间修改,单点查询 中我们有:
那么:
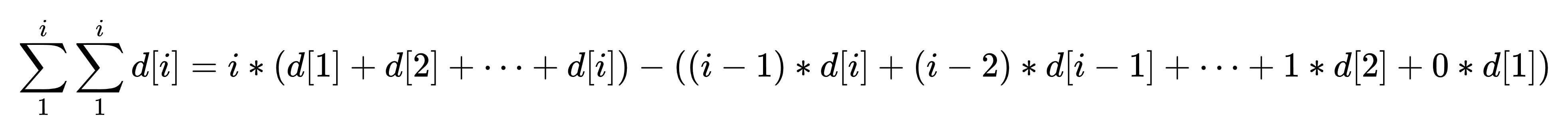
推出:
所以我们需要维护两个前缀和:
所以根据以上内容,综合上一节,我们可以给出区间修改的算法:
void add(int index,int e){
for(int i=index; i<=n; i+=lowbit(i)){
d[i][0] += e; //d[i]
d[i][1] += (index-1)*e; //(i-1)*d[i]
}
}
//a[i~j] + e
void change(int i,int j,int e){
add(i,e);
add(j+1,-e);
}区间查询:
根据之前的公式,我们可以得出区间查询的方案:
//查询d[index][num]的前缀和
int find(int index, int num){
int ans = 0;
for(int i=index; i;i-=lowbit(i))
ans += d[i][num];
return ans;
}
//查询a[i]的前缀和
int sum(int i){
return (i)*find(i,0) - find(i,1) //i*M-N
}二维树状数组:
当一维树状数组拓展到二维时:
t[i][j] =
a[1][1] + a[1][2] + a[1][3] + ··· +a[1][j] +
a[2][1] + a[2][2] + a[2][3] + ··· +a[2][j] +
a[3][1] + a[3][2] + a[3][3] + ··· +a[3][j] +
···
a[i][1] + a[i][2] + a[i][3] + ··· +a[i][j]
可以发现t[i]从一个值变成个了一个树状数组,可以理解为t是一个大的树状数组,其中每个元素t[i]也是一个树状数组,对于小树状数组t[i],其中的元素t[i][j]是一个整数。
单点修改、区间查询:
单点修改:
可以从一维进行类比推理,一样是只修改受影响的元素
具体介绍在代码注释中体现:
//a[i][j] + e
void add(int index_i,int index_j,int e){
for(int i=index_i; i<=n; i+=lowbit(i)){ //枚举受影响的树状数组t[i]
for(int j=index_j; j<=m; j+=lowbit(j)){ //枚举修改树状数组t[i]中受影响的元素
t[i][j] += e;
}
}
}区间查询:
//求a[1][1]~a[index_i][index_j]的和
int sum(int index_i,int index_j){
int ans = 0;
for(int i=index_i; i; i-=lowbit(i))
for(int j=index_j; j; j-=lowbit(j))
ans += t[i][j];
return ans;
}二维下如果要求某个特定的区间,和一维相比更加复杂一些:
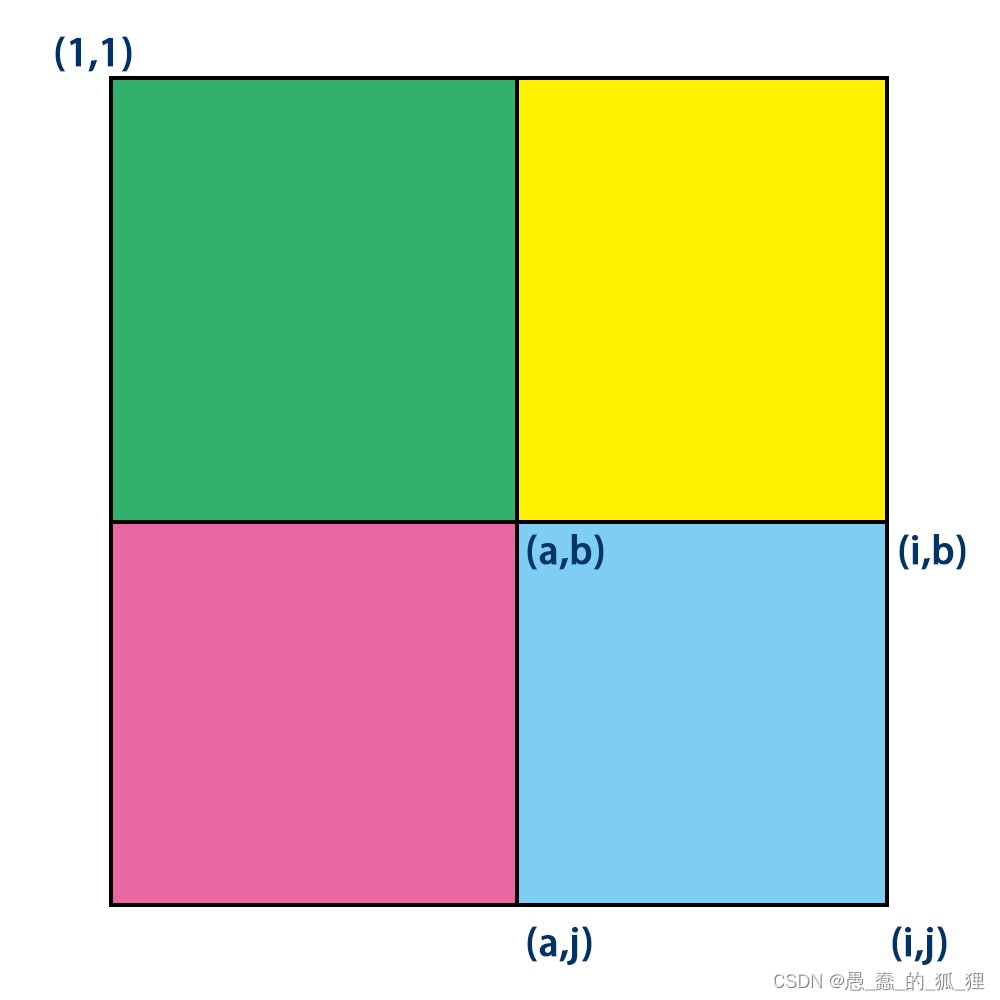
例如我们需要求(a,b) 到 (i,j) 这个区间的和,但我们只有从(1,1)开始到任意点的和:记作sum(i,j)。
这时我们可以得出(减1是因为边界也是要算进和里面的):
(a,b) 到 (i,j) 这个区间的和 = sum(i,j)-sum(a-1,j)-sum(i,b-1)+sum(a-1,b-1)
为什么要加上sum(a-1,b-1)呢?因为我们在-sum(a-1,j)-sum(i,b-1)的时候减去了两个sum(a-1,b-1),要补回来一个。
所以,求任意区间和的算法为:
//求(x1,y1)~(x2,y2)的区间和
int find(int x1,int y1,int x2,int y2){
return sum(x2,y2) - sum(x1-1,y2) - sum(x2,y1-1) + sum(x1-1,y1-1);
}区间修改、单点查询:
区间修改:
区间修改还是逃不出差分的思想,但是二维下的差分和一维相比略有区别:
如果要增加a[i][j] ~ a[x][y]的值那么对d数组的操作为:
d[i][j] + e
d[x][y+1] - e
d[x+1][y] - e
d[x+1][y+1] + e
可以结合之前的知识思考一下,还是很好理解的。
可以得出算法为:
void add(int index_i,int index_j,int e){
for(int i=index_i; i<=n; i+=lowbit(i))
for(int j=index_j; j<=m; j+=lowbit(j))
d[i][j] += e;
}
//a[x1][y1]~a[x2][y2] + e
void change(int x1,int y1,int x2,int y2,int e){
add(x1,y1,e);
add(x2+1,y2,-e);
add(x2,y2+1,-e);
add(x2+1,y2+1,e);
}单点查询:
//查询a[x][y]的值
int find(int x,int y){
int ans = 0;
for(int i=x; i; i-=lowbit(i))
for(int j=y; j; j-=lowbit(j))
ans += d[i][j];
return ans;
}区间修改、区间查询:
区间修改:
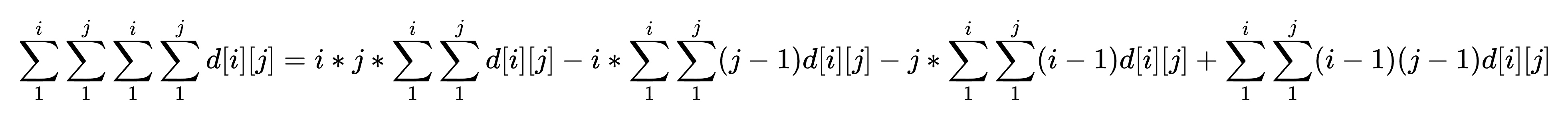
所以我们需要维护四个前缀和:
void add(int index_i,int index_j,int e){
for(int i=index_i; i<=n; i+=lowbit(i)){
for(int j=index_j; j<=n; j+=lowbit(j)){
d[i][j][0] += e; //d[i]
d[i][j][1] += (index_j-1)*e; //(j-1)*d[i]
d[i][j][2] += (index_i-1)*e; //(i-1)*d[i]
d[i][j][3] += (index_i-1)*(index_j-1)*e; //(i-1)*(j-1)*d[i]
}
}
}
//a[x1][y1]~a[x2][y2] + e
void change(int x1,int y1,int x2,int y2,int e){
add(x1,y1,e);
add(x2+1,y2,-e);
add(x2,y2+1,-e);
add(x2+1,y2+1,e);
}区间查询:
//查询d[index_i][index_j][num]的前缀和
int find(int index_i,inde index_j,int num){
int ans = 0;
for(int i=index_i; i; i-=lowbit(i))
for(int j=index_j; j; j-=lowbit(j))
ans += d[i][j][num];
return ans;
}
//查询a[i][j]的前缀和
int sum(int i,int j){
//i*j*M - i*N -j*P + Q
return (i*j)*find(i,j,0) - i*find(i,j,1) - j*find(i,j,2) + find(i,j,3)
}





















 106
106











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








