背包问题详解

前言

本文主要讲解01背包问题，读者如果能完全搞懂01背包，那么稍作思考也能解决完全背包、多重背包问题。至于分组背包、有依赖的背包等问题博主也没有继续深入，但是应该都是在01背包的基础上拓展，读者若有兴趣可查阅其他文章。

01背包问题

有n个物品，每个物品有且仅有1件，每个物品有重量和价值两个属性，现在有一个固定容量的背包，要将这些物品放入背包内，使得背包内物品总价值最大，问要如何放？
举个具体的例子，有5件物品，物品的重量和价值如下所示：

物品编号	重量	价值
1	2	4
2	3	3
3	5	8
4	4	5
5	2	2

背包容量为5时应该怎么放？

解决思路

对于n个物品w容量的背包或许毫无头绪。可以从简单的开始思考，如果是只有1个物品w容量呢？那就很简单了。容量大于等于物品重量时放入，小于时无法放入，这很好理解吧。列出容量与价值的表格如下：
该表格的含义是当有1件物品、背包容量为w时，背包能装的最大价值

可以看到，当背包容量大于2时，能装的最大价值只能是4，因为只有一件物品，背包再大也没东西可以装。

在此问题的基础上拓展一下，当存在编号1、2两件物品时，还是按照之前的思路，只考虑物品2能不能放入，先列出一个临时表格如下：

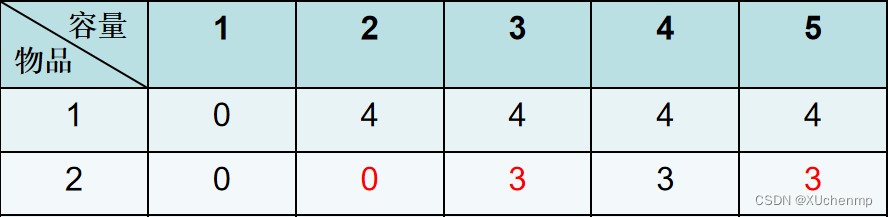
注意表格中三个标红的地方。

1. 当背包容量为2时，虽然不能放入2号物品，但是可以放入1号物品，所以第2行第2列应该填4。含义是当同时存在物品1、2，背包容量为2时，最大价值为4。
2. 当背包容量为3时，虽然可以放入物品2，但是放入物品2后背包容量剩余0，无法再放入其他物品，此时背包的价值是3；如果不放入，背包容量为3，只存在物品1时，最大价值为4；4>3，所以选择不放入，第2行第3列填4。**含义是当同时存在物品1、2，背包容量为3时，最大价值为4。**容量为4时同理。
3. 当背包容量为5时，选择放入物品2，此时背包剩余容量为2，然后发现只存在物品1、容量为2时最大价值为4，此时背包总价值为3+4=7；如果不放入，背包容量为5，只存在物品1时，最大价值为4；7>4，所以选择放入物品2，第五列填7。
   更正后的表格为：
   该表格的含义是当有1、2两件物品、背包容量为w时，背包能装的最大价值
   
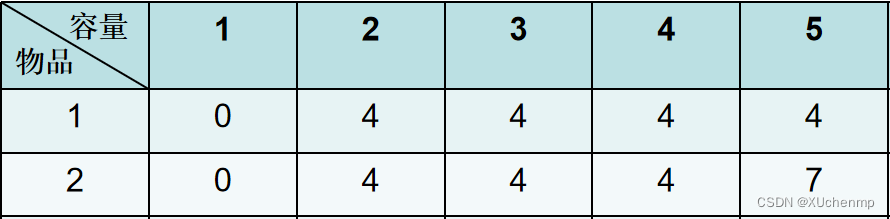
   多件物品与两件物品思路一样，往下继续计算便能得到最终的表格
   当有1、2、3、4、5五件物品、背包容量为w时，背包能装的最大价值
   

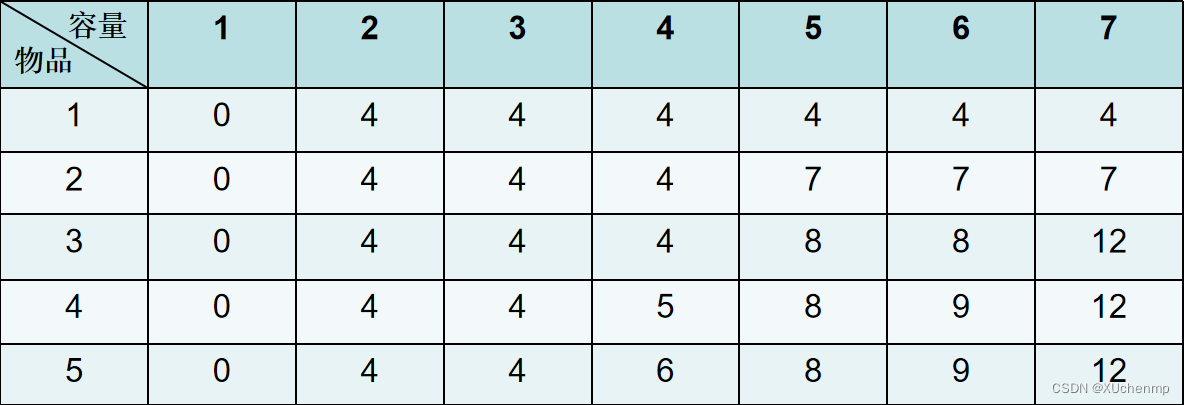
上面说的一堆东西可以凝练成一个东西，那就是状态转移方程
01背包的状态转移方程为$v[i][j]:\{\begin{array}{l}v[i-1][j]j<item[i].weight\\ Max(v[i-1][j],item[i].value+v[i-1][j-item[i].weight])j>=item[i].weight\end{array}$

代码实现

需要注意的是当遍历第一件物品并且 j < item[i].weight时取v[i-1]可能会出现数组越界或者空指针异常等问题；而且计算机是从0开始计数，人类的习惯是从1开始计数；所以为了防止程序异常和便于理解，v[0][j]表示没有物品时背包的价值。
网上大多数代码都是只输出最大价值，博主代码除了输出最大价值外，还输出了具体是拿哪几件物品（多个方案时只输出一个）。前面主要是测试用例和实体类定义，觉得啰嗦可以直接跳到88行看核心方法。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Main {
    public static void main(String[] args) {
        List<Item> items = new ArrayList<>();
        items.add(new Item(2,4));
        items.add(new Item(3,3));
        items.add(new Item(5,8));
        items.add(new Item(4,5));
        items.add(new Item(2,2));
//        items.add(new Item(7,21));
//        items.add(new Item(2,18));
//        items.add(new Item(6,9));
//        items.add(new Item(3,15));
//        items.add(new Item(5,6));
        Backpack res1 = backpack_0_1(items, 7);
        String itemString = Arrays.toString(res1.getItems().toArray());
        System.out.println(String.format("取物品%s,能得到最大价值%s",itemString, res1.getValue()));
    }

    public static class Backpack {
        // 背包中存放的物品编号
        private List<Integer> items = new ArrayList<>();
        // 物品总价值
        private int value = 0;

        public List<Integer> getItems() {
            return items;
        }

        public void setItems(List<Integer> items) {
            this.items = items;
        }

        public int getValue() {
            return value;
        }

        public void setValue(int value) {
            if (value < 0) {
                throw new RuntimeException("物品价值不能小于0");
            }
            this.value = value;
        }
    }

    public static class Item {
        private int volume;
        private int value;

        public Item() {}
        public Item(int volume, int value) {
            if (volume <= 0) {
                throw new RuntimeException("物品体积必须大于0");
            }
            if (value <= 0) {
                throw new RuntimeException("物品价值必须大于0");
            }
            this.volume = volume;
            this.value = value;
        }

        public int getVolume() {
            return volume;
        }

        public void setVolume(int volume) {
            if (volume <= 0) {
                throw new RuntimeException("物品体积必须大于0");
            }
            this.volume = volume;
        }

        public int getValue() {
            return value;
        }

        public void setValue(int value) {
            if (value <= 0) {
                throw new RuntimeException("物品价值必须大于0");
            }
            this.value = value;
        }
    }

    public static Backpack backpack_0_1(List<Item> items,Integer backpackVolume){
        if (backpackVolume < 0) {
            throw new RuntimeException("背包体积不能小于0");
        }
        if (backpackVolume == 0 || items.size() == 0) {
            return new Backpack();
        }
        // 为了便于理解，在第0个位置填充null，保证第n个物品在items[n]的位置
        items.add(0,null);
        Backpack[][] table = new Backpack[items.size()][backpackVolume + 1];
        // 从体积为1开始遍历每一件物品
        for (int i = 1;i <= backpackVolume;i++) {
            for (int j = 1;j < items.size();j++) {
                Item item = items.get(j);
                // 不存在该物品时，容量为i时背包的最优解
                Backpack bestBackpack = table[j-1][i] == null ? new Backpack() : table[j-1][i];

                // 物品体积大于当前背包体积，不放入物品
                if (item.getVolume() > i) {
                    table[j][i] = bestBackpack;
                } else {
                    // 剩余体积
                    int residueVolume = i - item.getVolume();
                    // 剩余体积能装的最大价值
                    Backpack residueBestBackpack = table[j - 1][residueVolume] == null ? new Backpack() : table[j - 1][residueVolume];
                    int value =  residueBestBackpack.getValue();
                    // 如果放入后的价值大于放入前的价值，则放入该物品。否则不放入
                    if (item.getValue() + value > bestBackpack.getValue()) {
                        Backpack backpack = new Backpack();
                        backpack.setValue(item.getValue() + value);
                        backpack.getItems().addAll(residueBestBackpack.getItems());
                        backpack.getItems().add(j);
                        table[j][i] = backpack;
                    } else {
                        table[j][i] = bestBackpack;
                    }
                }
            }
        }
        return table[items.size()-1][backpackVolume];
    }
}

完全背包问题与多重背包问题

如果能彻底搞懂01背包问题那么这两种背包问题相信大部分人都能想得出来。如果暂时没想到或许对比一下01背包问题和完全背包问题的状态转移方程就能明白了。
01背包$v[i][j]:\{\begin{array}{l}v[i-1][j]j<item[i].weight\\ Max(v[i-1][j],item[i].value+v[i-1][j-item[i].weight])j>=item[i].weight\end{array}$

完全背包$v[i][j]:\{\begin{array}{l}v[i-1][j]j<item[i].weight\\ Max(v[i-1][j],item[i].value+v[i][j-item[i].weight])j>=item[i].weight\end{array}$

没错，就只是v[i]和v[i-1]的不同。
01背包问题是每类物品有且仅有一件，如果选择放入该物品，那么该物品就没有了，所以就只能是 item[i].value + v[i-1][j-item[i].weight]；完全背包问题是每类物品有无限件，哪怕我选择放入该物品之后还可以继续放入物品，所以就是 item[i].value + v[i][j-item[i].weight]。
如果还有点懵，不如回想一下本文的第一个例子，只有一件物品时，01背包容量大于物品重量后价值不会发生变化。但是完全背包的价值会随着容量的扩大从而阶梯性的增加，因为当剩余又能够放入一件物品时价值就会增加。

至于多重背包问题也是在此基础上拓展，无非是多了一个什么时候取v[i]什么时候取v[i-1]的问题罢了，就留给读者自行思考了。