位运算基础知识归纳(持续更新)2024-9-27更新：位运算优先级，操作等；

现代计算机中，几乎都是二进制计算机，所有的数据都以二进制的形式存储在设备中。位运算就是直接对存储在内存中的数据的二进制位进行操作。在计算机中，每一个二进制位称为1个bit，单位简写做1b。通常8个bit为一个单位，称为字节(byte)，单位简写作1B。

在C++中表示二进制数一般使用0x前缀表示的十六进制形式，和二进制数有一一对应的关系，如0x5A，表示二进制数 01011010 。

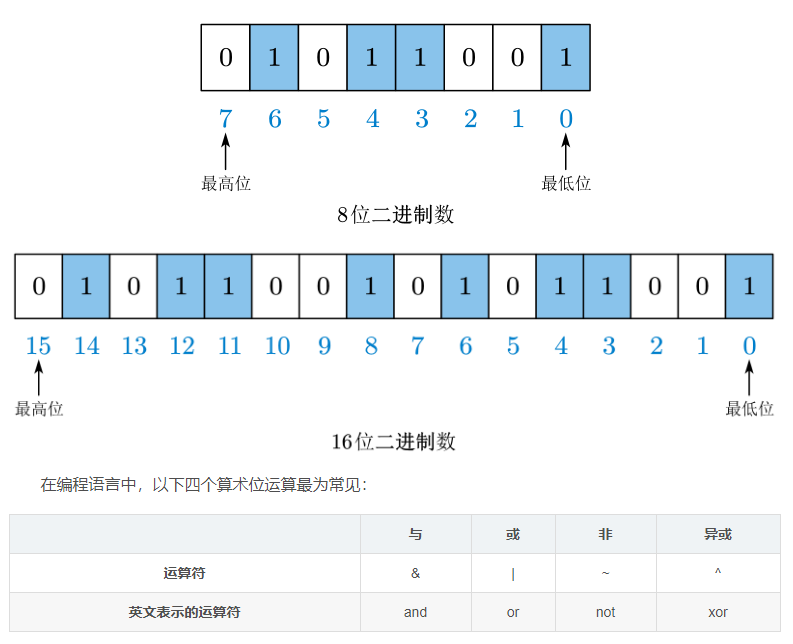
在 n 位二进制数中，我们一般称最低位为第 0位，最高位为 n − 1 位，总右到左依次是第 0 , 1 , 2 , ⋯   , n − 1 位 ，如下图所示：

（我们在计算时，一般使用的是 32位的int 类型(在个人计算机中，int一般为32位)，但为了便于将算法以图形表示，下面一般使用8位的二进制数来展示，而不是使用32位，否则位数太多，图形过小，不利于绘制和阅读。）

假设如果 A = 60，且 B = 13，现在以⼆进制格式表⽰，它们如下所⽰：

A = 0011 1100

B = 0000 1101

则

A&B = 0000 1100(与，对应位两个均为1则得1，否则为0)  

A|B = 0011 1101(或，对应位只要有一个为1则得1)

A^B = 0011 0001(异或，对应位相同为0，不同为1)

~A  = 1100 0011（非，取反，即0变1，1变0）

<< ⼆进制左移运算符。左操作数的值向左移动右操作数指定的位数。 A << 2 将得到 240，即为 1111 0000，每左移一位，相当于乘2。

>> ⼆进制右移运算符。左操作数的值向右移动右操作数指定的位数。 A >> 2 将得到 15，即为 0000 1111，每右移一位，相当于除2。

注意以下⼏点：

1． 在这6种操作符，只有~取反是单⽬操作符，其它5种都是双⽬操作符。

2． 位操作只能⽤于整形数据，对float和double类型进⾏位操作会被编译器报错。

3． 对于移位操作，右移时⾼位是补符号位。如下⾯代码会输出-4和3。

因为15=0000 1111(⼆进制)，右移⼆位，最⾼位由符号位填充将得到0000 0011即3。-15 = 1111 0001(⼆进制，补码形式)，右移⼆位，

最⾼位由符号位填充将得到1111 1100即-4（见注1）。

int a = -15, b = 15;

printf("%d %d\n", a >> 2, b >> 2);

4． 位操作符的运算优先级⽐较低，尽量使⽤括号来确保运算顺序，否则很可能会得到莫明其妙的结果。⽐如要得到像

1，3，5，9这些2^i+1的数字。写成int a = 1 << i + 1;是不对的，程序会先执⾏i + 1，再执⾏左移操作。应该写成int a = (1<< i) + 1;

又例如 if (a&b!=0)    ，会先判断(b!=0)。

5． 另外位操作还有⼀些复合操作符，如&=、|=、 ^=、<<=、>>=。

位运算的应用：

 判断偶数，判断最低位是0还是1即可，⽐求模快

x % 2 != 0 //x正负都可以判断；不⽤x%2 == 1，因为如果x为负奇数，x%2=-1

(x & 0x1) == 0

例如：

int x;

int main()

{

   cin>>x;

   if((x & 0x1)==0) cout<<"yes"; 

   else cout<<"no";

   return 0;

}

2.两个数的交换

a = a^b;//a变为⼀个相同为0，相异为1的结果 

b = a^b;//该结果和b做运算，得到原来的a 

a = a^b;//该结果和a做运算，得到原来的b

再来个实例说明下以加深印象。int a = 13, b = 6;

a的⼆进制为1101(⼆进制)

b的⼆进制为 110(⼆进制)

第⼀步 a^=b a = 1101 ^ 110 = 1011;

第⼆步 b^=a b = 110 ^ 1011 = 1101;即b=13

第三步 a^=b a = 1011 ^ 1101 = 110;即a=5

3.lowbit运算

lowbit 运算 是位运算中比较重要的运算方式，用于计算一个二进制数最低位的1。

lowbit 即二进制数最低位1所对应的值。

如，二进制数 0b01011000最低的 1是在第3位，对应值为0b1000，即8。

lowbit运算的实现

一个数的lowbit值，即一个数的最低位，可通过如下操作取出，复杂度为 O(1)：

假设原来的数是a，对a取反加1得到~a+1，原数a和~a+1进行位与操作，就得到了lowbit值，即lowbit(a) = a & (~a + 1)。

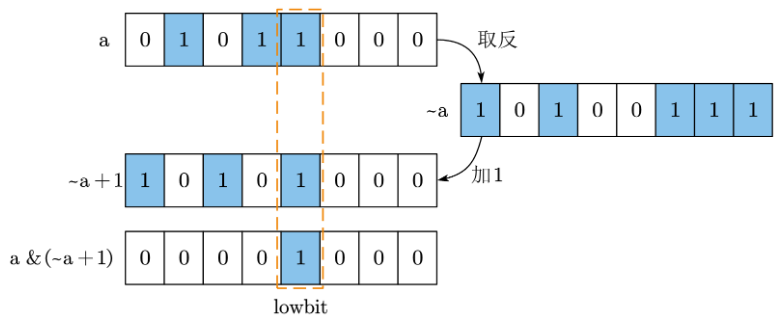
当这个数是0，没有最低位1的时候，结果为0。

因为取反加1就是一个数的相反数的补码，因为lowbit也写作

lowbit(a)=a&(-a)

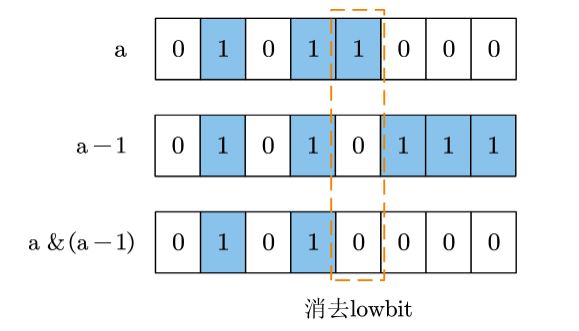
一个数消去它的lowbit位，由上面的lowbit求法，直接减去它的lowbit值即可。

即 a-(a&-a)

也可以由a&(a-1)得到

4.求整数的⼆进制表⽰中1的个数，不⽤⼀个⼀个的移位判断

#include <bits/stdc++.h>

using namespace std;

int x,cnt;

int main()

{

   cin>>x;

   while(x!=0)

   {

   cnt++;

   x&=x-1;//将最右边的1置为0；正负都可计算，负数是按照补码计算的，最后的符号位也被统计

   } 

   cout<<cnt;

   return 0;

}

5.判断一个数是否2的N次⽅次

题⽬要求：⽤⼀个表达式，判断⼀个数X是否是2的N次⽅，即2,4,8,16……等，要求不可以⽤循环语句。

解析：2,4,8,16这样的数转化成⼆进制是10,100,1000,10000。

如果X减去1后（低⼀位并且⼆进制的每⼀位都是1），这个数与X做与运算，答案若是0，则X是2的N次⽅。

所以答案是：!(x&(x-1))

即可写成：if !(x&(x-1)) cout<<"yes"

例题：

第4题     优秀的拆分(csp2020入门级1) 

一般来说，一个正整数可以拆分成若干个正整数的和。例如，1=1，10=1+2+3+4等。 

对于正整数n的一种特定拆分，我们称它为“优秀的”，当且仅当在这种拆分下，n被分解为了若干个不同的2的正整数次幂。注意，一个数x能被表示成2的正整数次幂，当且仅当x能通过正整数个2相乘在一起得到。 

例如，10=8+2=23+21是一个优秀的拆分。但是7=4+2+1=22+21+20就不是一个优秀的拆分，因为1不是2的正整数次幂。 

现在，给定正整数n，你需要判断这个数的所有拆分中，是否存在优秀的拆分。若存在，请你给出具体的拆分方案。 

#include<bits/stdc++.h>
using namespace std;
int x;
long long y;
int main()
{
	cin>>x;
	if(x%2==1)
	{
		cout<<-1;
		return 0;
	}
	for(int i=1;;i++)
	{
		if(pow(2,i)>x)
		{
			y=pow(2,i-1);
			cout<<y<<" ";
			x-=y;
			i=1;
		}
		if(pow(2,i)==x)
		{
			y=pow(2,i);
			cout<<y;
			x=0;
		}
		if(x==0) return 0;
	}
}

位运算的性质
 运算符的优先级
优先级需要弄清楚，如果不太清楚可以加小括号确保是想要的运算顺序，这里只是相对优先级，即只是和一些常用的算术运算符做比较。

优先级    运算符    结合方向
1    − （符号运算符） , ∼ （取反运算符）， + + （自增）， − − （自减） -（符号运算符）,\sim（取反运算符）， ++（自增），--（自减）−（符号运算符）,∼（取反运算符），++（自增），−−（自减）    从右到左
2    ∗ （乘） , / （除） , % （取余） *（乘）,/（除）,\%（取余）∗（乘）,/（除）,%（取余）    从左到右
3    + （加） , − （减） +（加）,-（减）+（加）,−（减）    从左到右
4    < < （左移）， > > （右移） <<（左移），>>（右移）<<（左移），>>（右移）    从左到右
5    > （大于） , < ( 小于 ) , > = ( 大于等于 ) , < = ( 小于等于 ) >（大于）,<(小于),>=(大于等于),<=(小于等于)>（大于）,<(小于),>=(大于等于),<=(小于等于)    从左到右
6    = = ( 等于 ) , ! = （不等于） ==(等于),!=（不等于）==(等于),!=（不等于）    从左到右
7    & （按位与） \&（按位与）&（按位与）    从左到右
8    ∧ ( 按位异或 ) \wedge (按位异或)∧(按位异或)    从左到右
9    ∣ ( 按位或 ) |(按位或)∣(按位或)    从左到右
2.2 位运算符的运算律
公式名称    运算规则
交换律    A & B = B & A , A ∧ B = B ∧ A A\&B=B\&A ,A\wedge B=B\wedge AA&B=B&A,A∧B=B∧A
结合律（注意结合律只能在同符号下进行）    ( A & B ) & C = A & ( B & C ) (A\&B)\&C=A\&(B\&C)(A&B)&C=A&(B&C)
等幂律    A & A = A ， A ∣ A = A A\&A=A，A|A=AA&A=A，A∣A=A
零律    A & 0 = 0 A\&0=0A&0=0
互补律（注意，这不同于逻辑运算）    A & ∼ A = 0 , A ∣ ∼ A = − 1 A\&\sim A=0,A|\sim A=-1A&∼A=0,A∣∼A=−1
同一律    A ∣ 0 = A ， A ∧ 0 = A A|0=A，A\wedge 0 =AA∣0=A，A∧0=A
以上仅为已证明的运算律（可能存在遗漏），其余的博主均认为是不符合不成立的，注意：千万不要将逻辑运算的运算律或者其他的运算律与这混为一谈。

3 位运算高级操作
如下表，请读者认真阅读理解，在阅读的过程中可以对示例进行运算。

功能    示例    位运算
去掉最后一位    0100 − > 0010 0100->00100100−>0010    x > > 1 x>>1x>>1
在最后加一个0 00    0100 − > 1000 0100->10000100−>1000    x < < 1 x<<1x<<1
在最后加一个1    0100 − > 1001 0100->10010100−>1001    ( x < < 1 ) + 1 (x<<1)+1(x<<1)+1
将最后一位变为1 11    0100 − > 0101 0100->01010100−>0101    x ∣ 1 x|1x∣1
将最后一位变为0 00    0101 − > 0100 0101->01000101−>0100，这里实际上就是先确保最低位变为1 11，再减去1 11。    ( x ∣ 1 ) − 1 (x|1)-1(x∣1)−1
最后一位取反    0100 − > 0101 0100->01010100−>0101 ，利用异或性质，其中除最后一位其余不变。    x ∧ 1 x\wedge1x∧1
把右数的第k kk位变为1 11    0001 − > 1001 , k = 4 0001->1001,k=40001−>1001,k=4    x ∣ ( 1 < < ( k − 1 ) ) x|(1<<(k-1))x∣(1<<(k−1))
把右数的第k kk位变为0 00    1001 − > 0001 , k = 4 1001->0001,k=41001−>0001,k=4，这个操作实际上就是先得到了1000 10001000，然后取反得到0111 01110111，最后利用按位与的性质其余位不变，最高位为0 00    x & ( ∼ ( 1 < < ( k − 1 ) ) ) x\&(\sim(1<<(k-1)))x&(∼(1<<(k−1)))
把右数的第k kk位取反    1000 − > 0000 , k = 4 1000->0000,k=41000−>0000,k=4，利用异或性质    x ∧ ( 1 < < ( k − 1 ) ) x\wedge (1<<(k-1))x∧(1<<(k−1))
由于表长限制，这里接下表继续：

功能    示例    位运算
取末k kk位    1011 − > 0011 , k = 2 1011->0011,k=21011−>0011,k=2    x & ( ( 1 < < k ) − 1 ) x\&((1<<k)-1)x&((1<<k)−1)
取右数的第k kk位    1011 − > 0001 , k = 4 1011->0001,k=41011−>0001,k=4，右移k − 1 k-1k−1位则是去掉了最后的k − 1 k-1k−1位，我们利用按位与即可将其提取出来    x > > ( k − 1 ) & 1 x>>(k-1)\&1x>>(k−1)&1
把末k kk位全变为1 11    1000 − > 1111 , k = 3 1000->1111,k=31000−>1111,k=3    x ∣ ( ( 1 < < k ) − 1 ) x|((1<<k)-1)x∣((1<<k)−1)
把末k kk位取反    0101 − > 1010 , k = 4 0101->1010,k=40101−>1010,k=4    x ∧ ( ( 1 < < k ) − 1 ) x\wedge ((1<<k)-1)x∧((1<<k)−1)
把右边连续的1 11变为0 00    0111 − > 0000 0111->00000111−>0000 ，注意是右起连续的1 11    x & ( x + 1 ) x\&(x+1)x&(x+1)
把右起的第一个0 00变为1 11    0011 − > 0111 0011->01110011−>0111    x ∣ ( x + 1 ) x|(x+1)x∣(x+1)
把右起连续的0 00变为1 11    1000 − > 1111 1000->11111000−>1111，注意是右起连续的0 00    x ∣ ( x − 1 ) x|(x-1)x∣(x−1)
取右边连续的1 11    1011 − > 0011 1011->00111011−>0011    ( x ∧ ( x + 1 ) ) > > 1 (x\wedge (x+1))>>1(x∧(x+1))>>1
去掉右起的第一个1 11的左边    1101 − > 0001 1101->00011101−>0001    x & ( x ∧ ( x − 1 ) ) x\&(x\wedge (x-1))x&(x∧(x−1))
当然，这里只是一些常用的，并不是全部，位运算的神奇远不止于此。

 负数的位运算
首先，我们要知道，在计算机中，运算是使用的二进制补码，而正数的补码是它本身，负数的补码则是符号位不变，其余按位取反，最后再+ 1 +1+1得到的， 例如：

15 1515,原码:00001111   00001111\space00001111 补码:00001111 0000111100001111

− 15 -15−15,原码:10001111   10001111\space10001111 补码:11110001 1111000111110001

那么对于负数的位运算而言，它们的操作都是建立在补码上的，得到的运算结果是补码，最后将补码结果转化成一个普通的十进制数结果。
但需要注意的是，对于有符号数的右移操作，不同的处理器架构可能有不同的规定。在某些架构中（如x86），如果对有符号数执行算术右移（arithmetic right shift），则高位空出来的位置会补上符号位；对于无符号数的右移操作，所有架构都遵循相同的规则：高位空出来的位置会补0。例如对于− 15 -15−15，其补码为11110001 , 11110001,11110001,右移一位( − 15 > > 1 ) (-15>>1)(−15>>1)得到的是11111000 1111100011111000，即− 8 -8−8，其他的同理。
在大多数现代处理器上，无论是有符号数还是无符号数，左移操作总是将空出来的低位补0。

这里我们介绍几个特殊的性质：

快速判断是否为− 1 -1−1

在链式前向星中，我们初始化h e a d headhead数组为− 1 -1−1，最后判断是否遍历完u uu的所有边时，即判断i ii是否为− 1 -1−1，我们直接用∼ i \sim i∼i即可。原因就在于− 1 -1−1的补码是11111111 1111111111111111，按位取反就变为00000000 0000000000000000，这实际上就是0 00。

取最低位的1 11，lowbit函数

也就是x & ( − x ) x\&(-x)x&(−x)，这在树状数组中起着巨大作用，这里指路一篇树状数组讲解b l o g blogblog:点这里，我们来证明一下，这里取x = 15 x=15x=15，对于15 & ( − 15 ) 15\&(-15)15&(−15)，我们知道，在补码上进行运算得到的是00000001 0000000100000001，需要注意二元运算的符号位我们需要进行运算。