阅读笔记：Safe Coverage of Moving Domains for Vehicles With Second-Order Dynamics

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

阅读笔记：Safe Coverage of Moving Domains for Vehicles With Second-Order Dynamics

安全性通过HJ可达性理论分析实现（CBF的问题在于存在震荡，对于需要c-cover的情况可能无法满足？）
均匀分布通过人工势场（artificial potential）和对准力（alignment force），控制达到期望的车间距和相对速度。

创新点在于：提出一种新的控制器，通过分布式控制，无需领导者，实现多智能体系统自发的完成对目标区域的覆盖。并通过HJ可达性保证过程的安全性。

一、HJ可达性详述

Hamilton–Jacobi (HJ) 可达性理论是一种用于碰撞避免的理论框架。在本文中，它被应用于确保多自主智能体之间的安全运动。HJ 可达性是基于博弈论的方法，其中两个智能体被建模为微分博弈的玩家：一个智能体（玩家1）作为“追踪者”（控制方），另一个智能体（玩家2）作为“逃避者”（扰动方）。

• Player 1（控制方）：试图将系统引向安全状态（或避免危险区域）。
• Player 2（扰动方）：试图将系统推向危险状态（最坏情况）。

HJ 可达性分析需要求解一个 Hamilton–Jacobi 偏微分方程（HJ PDE），以计算出向后可达集（Backward Reachable Set, BRS）。这个集合表示在最坏情况下，系统不可避免地到达危险状态的所有初始状态。通过求解 HJ PDE，可以得出一个最优控制策略，从而确保即使在最坏情况下，仍然能够避免碰撞。

• Backward Reachable Set (BRS)：表示从某个状态出发，最终无法避免到达危险区域的所有状态集合。
• Time-to-Reach (TTR)：从当前状态到达目标或危险区域所需的时间。

考虑一个两人零和博弈系统，其状态$z(t)$满足以下动力学方程：
$$\dot{z}(t)=f(z(t).u(t),d(t)),z(0)=x$$
其中，

• $u(t)$：控制方（Player 1）的输入。
• $d(t)$：扰动方（Player 2）的输入。
• $f$：系统动力学函数。

目标与策略

• Player 1 的目标是将系统状态远离危险区域（最大化安全性）。
• Player 2 的目标是将系统状态推向危险区域（最小化安全性）。
• 非预测性策略：Player 2 的行为不能依赖未来的信息。

Backward Reachable Set (BRS)

BRS 定义为系统中所有初始状态的集合，这些状态在最坏情况下会不可避免地进入危险区域。数学表达为：
B R S = { x ∈ R n   ∣   ∃ u ， ∀ d ， z ( t ) ∈ Γ D   a s   t → ∞ } BRS=\{ x\in R^n\ |\ \exists u ， \forall d ，z(t)\in\Gamma_D\ as \ t\rightarrow \infin\} BRS={x∈Rn ∣ ∃u，∀d，z(t)∈ΓD​ as t→∞}

Hamilton-Jacobi (HJ) 偏微分方程

最优控制输入

通过求解上述 HJ PDE，可以得到控制方的最优策略：
u ∗ ( z ) = a r g m i n u ∈ U m a x d ∈ D { − ∇ ϕ ( z ) ⋅ f ( z , u , d ) } u^*(z)=arg\underset{u\in U}{\mathrm{min}}\underset{d\in D}{\mathrm{max}}\{ -\nabla \phi(z)\cdot f(z,u,d)\} u∗(z)=argu∈Umin​d∈Dmax​{−∇ϕ(z)⋅f(z,u,d)}

HJ 可达性理论的步骤

最关键的一步就是如何获得$\varphi$，并由此得到最优控制策略。

应用实例

动力学相对形式

定义目标集合和可达集

解析求解方法

将上式进行化简可以得到：

控制策略

二、问题建模

动力学模型如下：

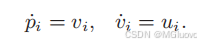
控制和状态限制、控制策略如下

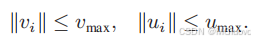
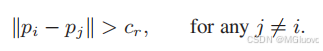
r-cover and r-subcover

若全部覆盖且满足智能体间距为r，智能体边界间距为r/2，则为cover，反之为subcover
考虑目标域移动速度恒定为$v_d$，则${\Omega }_t=\Omega +t{v}_d$表示移动目标域，定义目标域中心为$p_d$，则移动目标域为$p_d(t)=p_d+t{v}_d$

下面定义移动域集群

3.控制器设计

1. coverage controller

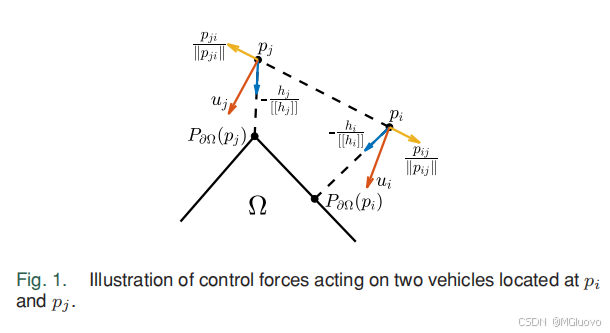
先考虑$v_d=0$的情况

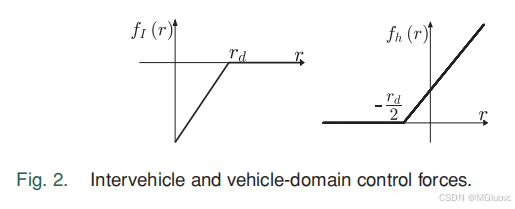
• $f_I$表示智能体间的斥力，在$r_d$内越近越大
• $f_h$表示智能体间的斥力，靠近边界时斥力上升，在边界外时则表现为引力

再考虑$v_d\ne 0$的情况

与$v_d=0$相比，需要设计一个机制来对齐移动域的速度以及智能体间的相对速度

受Cucker-Smale model启发，提出以下控制力

假设智能体知道其他智能体的速度和未知以及其到移动域的投影距离和$v_d$
智能体与邻居的一致性更强，而与距离更远的智能体的一致性更弱
$r_d=\sqrt{\frac{Area(\Omega )}{N}}$

结论： 由上述定义的动力学模型和控制输入可以保证Flocking with the moving target

4. HJ可达性分析

1.动力学模型：

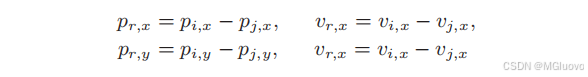
2.不安全区域

Γ D = { z : p r , x 2 + p r , y 2 ≤ c r 2 } \Gamma_D=\{z:p^2_{r,x}+p^2_{r,y} \le c^2_r\} ΓD​={z:pr,x2​+pr,y2​≤cr2​}

3. PDE

定义$\psi$为在最坏的情况下最终到达不安全区域的初始状态集合。
通过解析的方式构建：
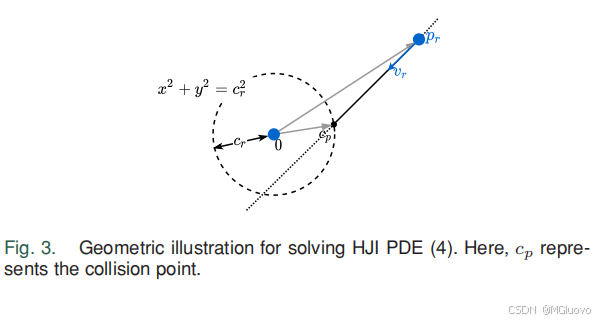
若存在碰撞，则存在一个碰撞点$c_p$如图所示，$c_p=(p_{r,x}+\psi (z)v_{r,x}，p_{r,y}+\psi (z)v_{r,u})$，并将其带入不安全区域中可以得到

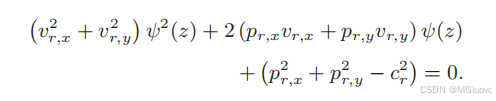
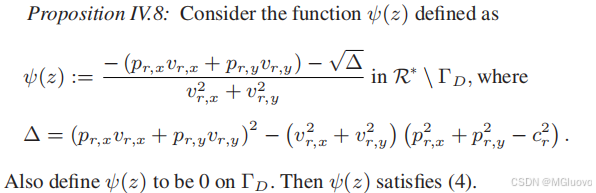
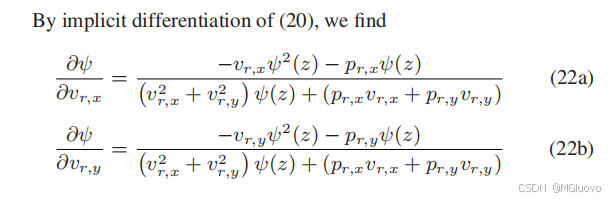
5.总的控制策略

定义安全时间为$t_{safety}$，若$\psi >t_{safety}$，证明不会发生碰撞，使用coverage controller；若$\psi \le t_{safety}$，证明可能发生碰撞，要用安全控制器，如果车辆检测到多个冲突，它将应用在该特定时间检测到的第一个冲突的控制策略。

（是否可以也涉及一个switching function，让两种控制器之间的转换更加平滑？
是否可以用CBF代替HJ可达性分析？保证两辆以上车辆的避免碰撞是一个未解决的问题