离散数学——图（无序积、图的表示、邻接点与边、图的分类、子图与补图、结点度数、握手定理）

一.无序积

图有无向图与有向图，为了描述无向图，首先给出无序积的概念：
定义设A，B为任意集合，称集合
$$A\&B=\{(a,b)|a\in A，b\in B\}$$为A与B的无序积，（a,b） 称为无序对

简单来说，就是对于序偶而言,<a,b>与<b,a>并不相同，但是在无序对里$（a，b）=（b，a）$

二.图的定义

一个图是一个序偶<V,E>,记为 G=<V,E>,其中:
(1) V = { v 1 , v 2 , . . . . v n } V=\{v_1,v_2,....v_n\} V={v1​,v2​,....vn​}是有限非空集合,$v_i$称为结点,简称点, $V$称为结点集.

(2)$E$是有限集合,称为边集.$E$中的每个元素都有$V$中的结点对与之对应,称之为边.

需要注意的是,定义中的结点对既可以是无序的,也可以是有序的.若边e与无序结点对$(u,v)$相对应,则称e为无向边,记为$e=(u,v)=(v,u)$,这时称u,v是边e的两个端点.若边e与有序结点对$<u,v>$相对应,则称e为有向边(或弧),记为$e=<u,v>$,这时称$u$为$e$的始点(或弧尾),$v$为$e$的终点(或弧头),统称为e的端点

三.图的表示

1.集合表示法与图形表示法

但是这两种表示方法都有各自的弊端，于是接下来引入邻接矩阵：

2.邻接矩阵法

定义：设图 G = < V , E > , 其中 V = { v 1 , v 2 , . . . , v n } , 并假定结点已经有了从 v 1 到 v n 的次序，则 n 阶方阵 A G = ( a i j ) n × n 称为 G 的邻接矩阵，其中： G=<V,E>,其中V=\{v_1,v_2,...,v_n\},并假定结点已经有了从v_1到v_n的次序，则n阶方阵A_G=(a_{ij})_{n×n}称为G的邻接矩阵，其中： G=<V,E>,其中V={v1​,v2​,...,vn​},并假定结点已经有了从v1​到vn​的次序，则n阶方阵AG​=(aij​)n×n​称为G的邻接矩阵，其中： $$a_{ij}=\{\begin{array}{ll}1& 若（v_i,v_j）\in E或<v_i,v_j>\in E（i,j=1,\mathrm{2...}n）\\ 0& 否则\end{array}$$
光看函数表示可能难以理解，接下来给出邻接矩阵的实际操作：

也就是说，对于无向图：如果两个结点之间有边的话，就写1，没有就写0
对于有向图，则要注意箭头方向，行表示箭头的起点，列表示箭头终点，例如：

对应的邻接矩阵就是：$$\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 1& 0& 1& 1& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 0\end{array}\right]$$

四.邻接点与邻接边

一些简单的特殊图：

其中，含有n个结点的图也称为n阶图
零图没有任何边，容易知道它的邻接矩阵为全0

五.图的分类

1.按边有无方向分类

2.按有无平行边分类

注意不要搞混了简单图和平凡图，简单图是无环的线图。平凡图是只有一个结点的零图

特别注意一下：在有向图中，连接两个相同的结点，但是方向相反的边，不是平行边！！

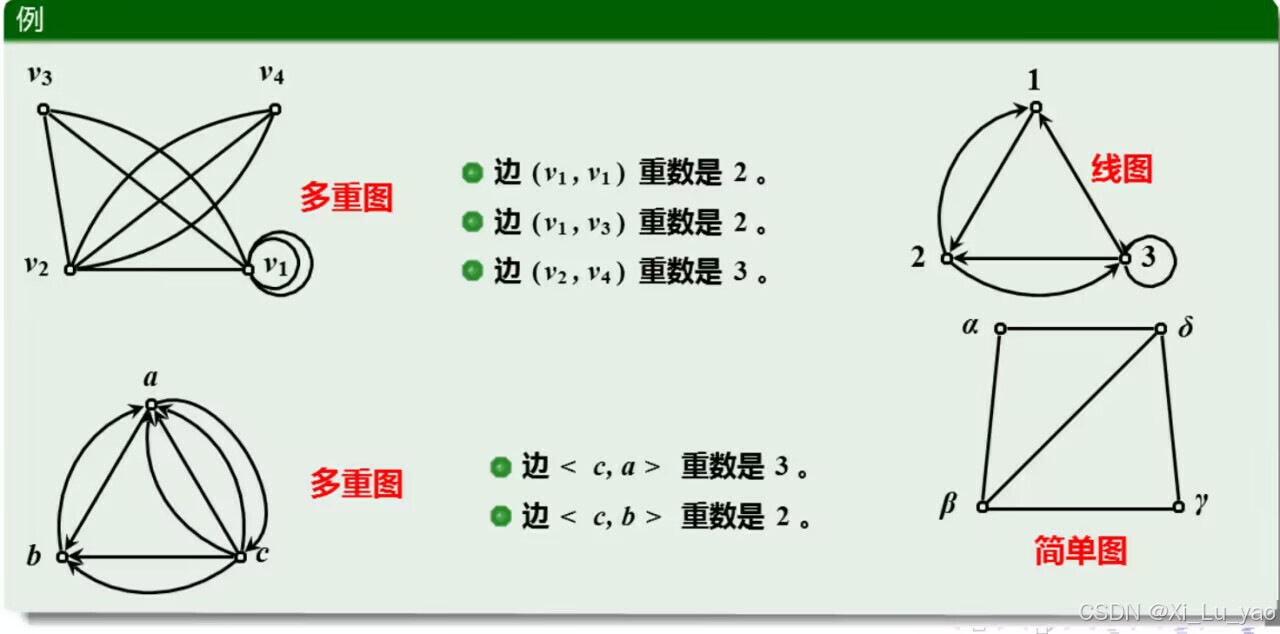
3.按边或结点是否含权分类

边有权值的赋权图:

边和结点都有权值：


$f表示结点，g表示边$，$<f,g>对应<V,E>$，方便记忆

六. 子图与补图

1.子图

(1)子图：$若V_1\subseteq V,E_1\subseteq E,则称G,是G的子图,记为G_1\subseteq G$

(2)真子图：$若G_1\subseteq G,且G\ne G(即V_1\subseteq V或E_1\subseteq E),则称G_1是G的真子图，记为G_1\subset G$

(3)生成子图：若$V_1=V,E_1\subseteq E,则称G_1是G的生成子图$。
通俗理解就是在原来的图上删边（可以删除0条边，也就是$E_1=E$时）

(4)导出子图：$设V_2\subseteq V且V_2\ne Ø$,$以V_2为结点集,以两个端点均在V_2中的边的全体为边集的G的子图,称为V_2导出的G的子图,简称V_2的导出子图.$
通俗理解就是在原图上删点，但是剩余的点的边关系要保留

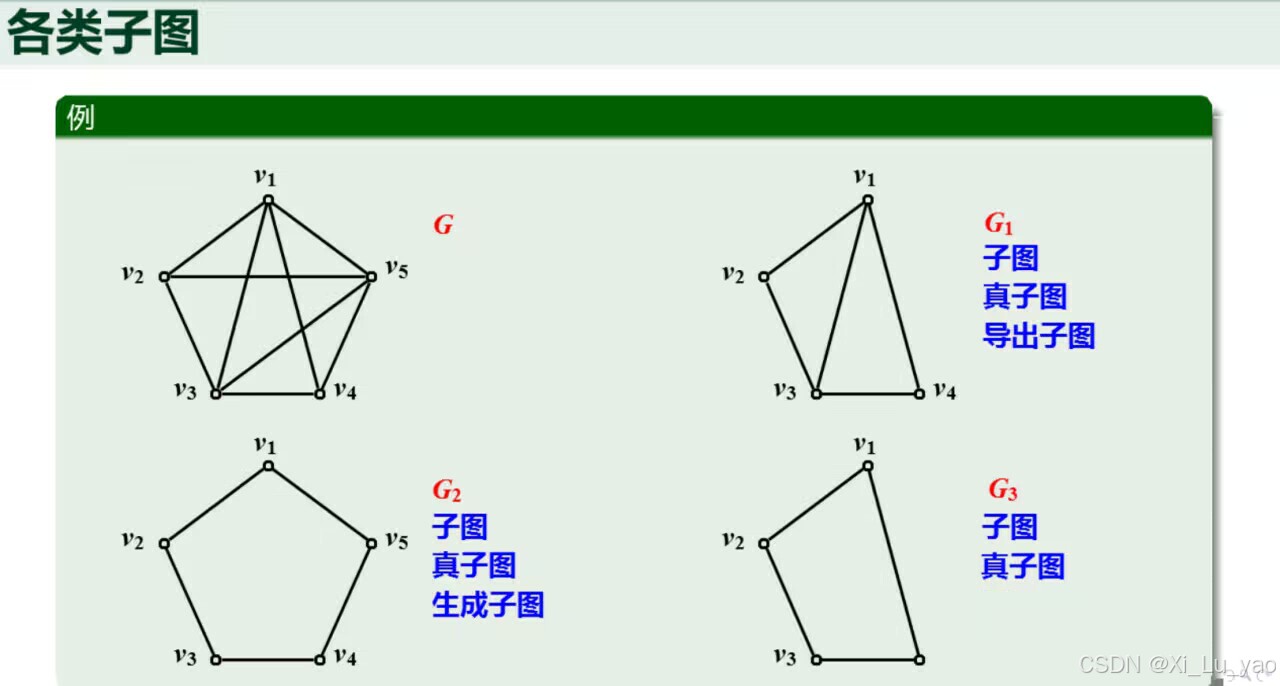
同时，G也是G自己的子图、生成子图、导出子图：

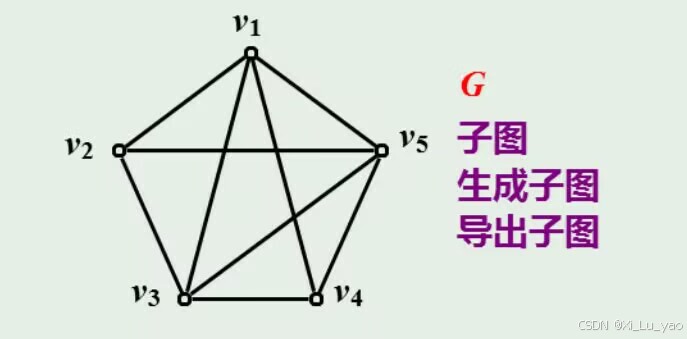
2.完全图与补图

这边解释5条边一定有3条在$G$或$\overline{\text{G}}$中：
1.若$G$有0条边，则$\overline{\text{G}}$中有5条边，而5>3，则$\overline{\text{G}}$中一定有三条边
2.若$G$有1条边，则$\overline{\text{G}}$中有4条边，同1中理由
3.若$G$有2条边，则$\overline{\text{G}}$中有3条边
4.若$G$有3（或4或5）条边，显然满足

七.结点度数与握手定理

记住：出正入负（与电路中的电流流入流出符号相反，不要搞混了）