每日两道leetcode

11. 盛最多水的容器 - 力扣（LeetCode）

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

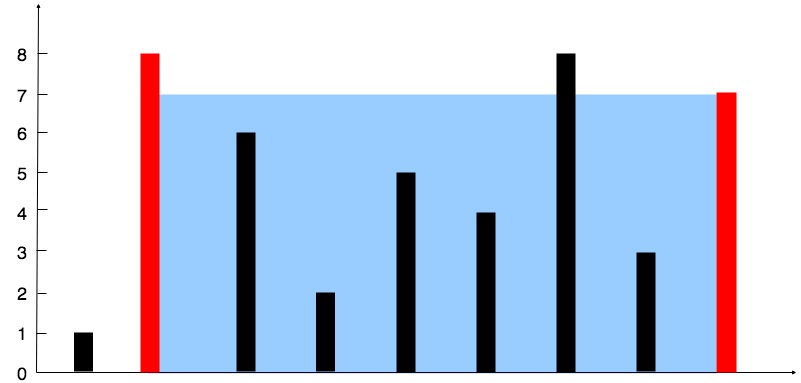
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

思路

1. 最先能想到的肯定是两个指针从同一端逐渐延伸或是分别从两端开始往里收缩，但是没想到怎么去延伸或收缩，最后还是参考了官方题解。
2. 其思路就是，指针从两端往里缩，每次都只移动较低的那一头，保持另一头的最高高度不变，而达成缩短一步进行探索的目的。
3. 直到两个指针相遇，输出过程中遇到的最大的面积即可。
4. 总结来说，关键要想好怎么贪心，我一开始采用同端扩展的方法，但是最后会受限于左节点的高度，所以是有问题的。双端收缩就需要判断该怎么贪心保证一次不要跨度过大，所以官方题解的思路确实好呢。

代码实现

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l = 0, r = height.size()-1, max_area = 0, area, distance;
        distance = r;
        while(l < r) {
            if(height[l] < height[r]) {
                max_area = max(max_area, distance * height[l]);
                l++;
            }
            else {
                max_area = max(max_area, distance * height[r]);
                r--;
            }
            distance--;
        }
        return max_area;   
    }
};

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。