柯西乘积定理（Cauchy Product Theorem）

柯西乘积

结论

在数学上，以法国数学家奥古斯丁·路易·柯西命名的柯西乘积，是指两组数列an，bn的离散卷积。

对两个严格的形式级数（不需要收敛）an，bn：

           

一般地，对于实数和复数，柯西乘积定义为如下的离散卷积形式：

            

啥叫形式？

• “形式”是指我们对级数运算时不考虑是否收敛，参见形式幂级数。
• 人们希望，通过对两组级数做实际卷积的有限和的类推，得到无穷级数。
• 就如同两个数列的和是有限范围一样做乘法。 在充分良态（well-behaved）的情况下，上述式子成立。而更重要的一点，尽管这两个无穷级数可能不收敛，它们的柯西乘积仍可能存在。（百度百科）

叽里咕噜说啥呢？

• “形式”，就是对级数做运算的时候，不管能不能得到一个确切的结果（也就是不考虑他是发射还是收敛），先算了再说。就跟形式幂级数一样，就只看式子的样子，也就是形式。
• 咋做运算呢？——就像我们平常算有限个数加起来再相乘那样，对两组无穷多个数加起来的级数（无穷级数 ）也做类似的操作。把两组级数按照一种特定方式（类似卷积，就是按一定规则把对应项乘起来再相加 ）相乘，得到一个新的无穷级数 。
• 如果各项数值变化比较规律，满足一些条件，这样相乘得到的式子是成立的。而且有意思的是，就算最开始那两个无穷级数加起来没有个确定的数（不收敛 ），按照这种方式乘出来的新级数（柯西乘积 ）却有可能是有意义的，能算出个结果来 。

此外，对以下两个级数相乘：

                                         

还可以表示为：

                                

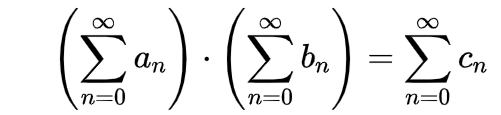
其中：

柯西划线法

        怎么记住这个公式？

        先将两个级数的项写出来，横着一排，竖着一排：

                ​​​​​​​       

        写上对应两个项数的乘积：

                           ​​​​​​​

        划线：

                    

        那么，当a级数有三项，b级数有三项的时候就可以下成下面这样：

                                        

        可以发现，对上面的第i行（i从0到4），都有：每一项的下标和都是i

        故：

        

     

推广

        两个从  n=0  开始的无穷幂级数，与相乘，得到的结果是一个新的无穷幂级数，其中新幂级数的第  n  项系数 是通过将  a  系列的前  n+1  项（即到）与  b  系列对应的项（ 即到)两两相乘再求和得到的，也就是 

                        

参考资料

柯西乘积_百度百科

张宇十八讲