博弈论入门--巴什博弈的推导与证明

巴什博弈:

巴什博弈是一种两人博弈，起源于20世纪初的法国。游戏开始时，有一堆物品，两人轮流取n个物品，每次可以取走1~m个物品，最少取一个，最多取m个，谁取走最后一个物品谁就赢了。巴什博弈的关键在于找到取胜策略，即先手能否必胜或必输。

首先我们分情况进行讨论：

          1.n<=m时：显然先手可以一次性取走所有石子 后手必输

          2.n=m+1时：先手无论怎么取石子 剩余的石子总是在区间[1,m]中 此时后手可以一次性拿完所有石子 先手必输

由这两个基本点我们是否可以推断当n=k（m+1）时，先手必输？ 我们先采用归纳法尝试证明我们的这个猜想

当n=6 m=2时，我们将整个情况画出来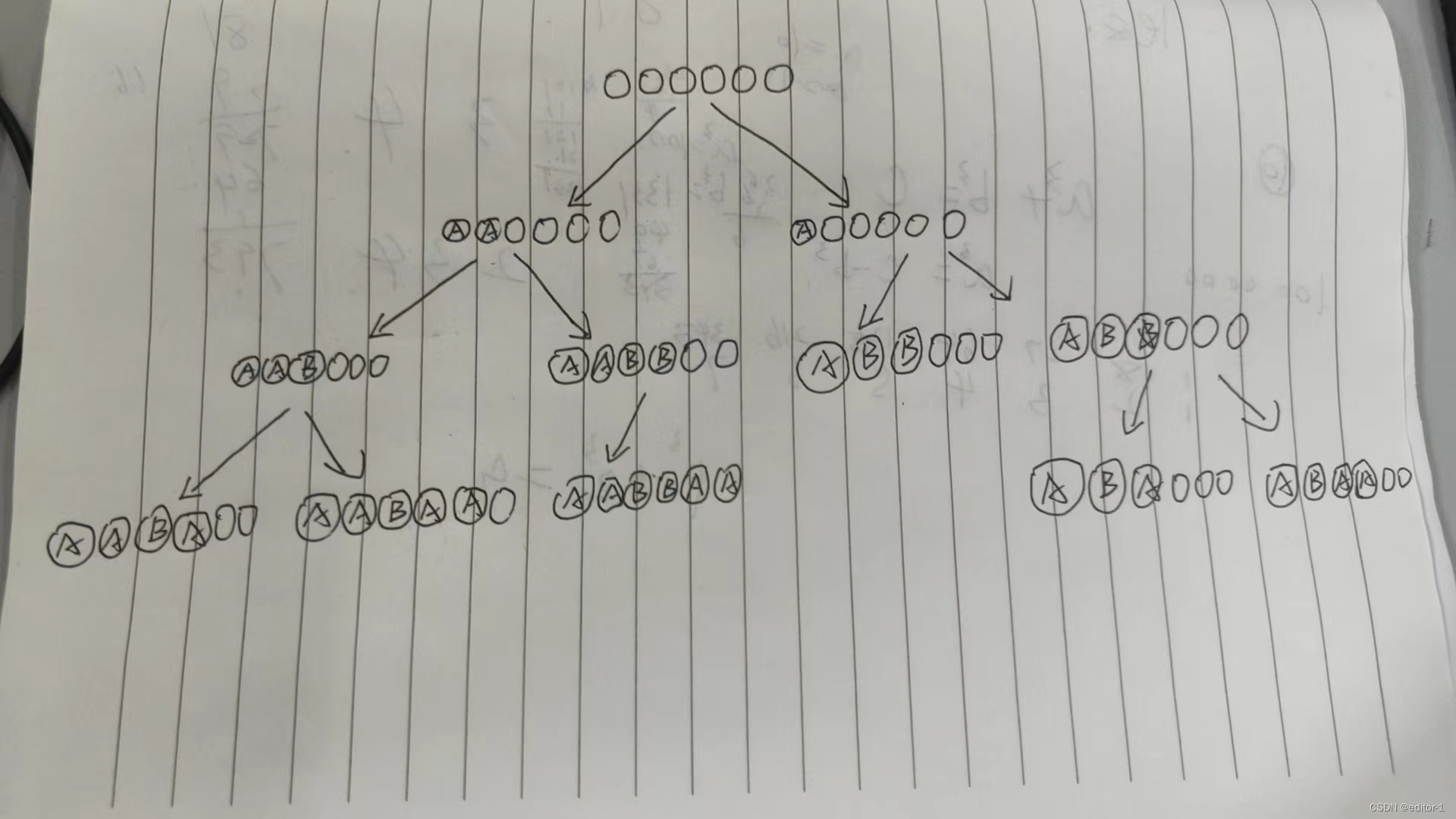

 这张图我只画到了胜负揭晓的状态 通过枚举我们发现如果后手B采取最优策略时 无论A怎么走都会陷入到只剩下(m+1)的状态 也就是先手必输局 那么我们可以由此推断得出当

                                              n=k(m+1)+s (m+1>s>0)

后手必输，因为先手采取最优策略拿走s个，让后手陷入了n=k*（m+1）局面 也就是上述的必败局势 通过归纳法我们证明出巴氏博弈的局面分析

                                         n%(m + 1) =  = 0，后手必胜。反之先手必胜

第二种证明方法--反证法

若 n≤k(m+1) 时命题成立

那么当k(m+1)<n≤(k+1)(m+1) 时，若 n=(k+1)(m+1)那么先手取完后剩下的物品数范围是 [k(m+1)+1,k(m+1)+m]后手可以正好取到 k(m+1)，由假设得先手必败

若 n<(k+1)(m+1) 那么先手可以取到 k(m+1)，由假设得此时后手必败先手必胜

证明完毕

通过巴什博弈我们可以对博弈论有初步的了解，了解到先手必胜这个概念 也就是说当先手必胜时，无论后者以什么样的策略进行反击都毫不影响最后的结果，这也就是必胜态 算是对博弈论的一个小入门