Datawhale组队学习2025.2 数学建模导论 Task 2: 权重生成与评价模型

Datawhale组队学习2025.2 数学建模导论 Task 2: 权重生成与评价模型

学习内容：

内容：@若冰（马世拓）

• 第7章 权重生成与评价模型
  • 引言
  • 7.1 层次分析法
    • 7.1.1 层次分析法的原理
    • 7.1.2 层次分析法的案例
  • 7.2 熵权分析法
    • 7.2.1 熵权分析法的原理
    • 7.2.2 熵权分析法的案例
  • 7.3 TOPSIS分析法
    • 7.3.1 一般的TOPSIS分析法
    • 7.3.2 改进的TOPSIS分析法
    • 7.3.3 TOPSIS分析法的案例
  • 7.4 CRITIC方法
    • 7.4.1 CRITIC分析法的原理
    • 7.4.2 CRITIC分析法的案例
  • 7.5 模糊综合评价法
    • 7.5.1 模糊综合分析法的原理
    • 7.5.2 模糊综合分析法的案
  • 7.6 秩和比分析法
    • 7.6.1 秩和比分析法原理
    • 7.6.2 秩和比分析法案例
  • 7.7 主成分分析法
    • 7.7.1 主成分分析法的原理
    • 7.7.2 主成分分析法的案例
  • 7.8 因子分析法
    • 7.8.1 因子分析法的原理
    • 7.8.2 因子分析法的案例
  • 7.9 数据包络分析法
    • 7.9.1 CCR数据包络模型
    • 7.9.2 BBC数据包络模型
    • 7.9.3 数据包络模型的实现
  • 7.10 评价模型总结
    • 7.10.1 指标体系的构建
    • 7.10.2 两大核心：权重生成与得分评价

---

学习时间：

• ddl: 2.16 凌晨03:00

---

学习笔记：

引言

这一章我们主要介绍评价模型。这类模型主要是用以解决对于一个目标不同方案之间比较或不同影响因素之间比较的问题。本章主要涉及到的知识点有：

• 层次分析法
• 熵权法
• TOPSIS分析法
• 模糊评价法
• CRITIC方法
• 主成分分析法
• 因子分析法
• 数据包络法

7.1 层次分析法

层次分析法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初提出的一种评价策略。这种策略虽然带有一定主观性，但非常奏效，也是在社会科学研究中经常使用的一类方法。

7.1.1 层次分析法的原理

首先，层次分析法的流程分五步走：

1.选择指标，构建层次模型。

2.对目标层到准则层之间和准则层到方案层之间构建比较矩阵。

3.对每个比较矩阵计算CR值检验是否通过CR检验，如果没有通过检验需要调整比较矩阵。

4.求出每个矩阵最大的特征值对应的归一化权重向量。

5.根据不同矩阵的归一化权向量计算出不同方案的得分进行比较。

下面我们就对其中的每个步骤进行详细的分析。

首先是选择指标。在一些问题当中，如果它明确了需要做一个评价类问题，有可能会给出一些评价的指标准则，但很多情况下它并不会给你明确的指标。这需要你查阅资料或者自己去构建。事实上当我们需要用层次分析法解决问题的时候所评价的准则量绝非空穴来风凭空杜撰，而是在经过大量文献考证或社会调查后选取的。如果不去查阅文献的话可能就得发放调查问卷或者使用德尔菲法去征求专家意见。所幸，这些指标都是可以通过查找以往文献得到的。指标按照一定的层级结构组织起来就构成了一个指标体系。

层次分析法的层次从何而来？注意，在层次分析法中一个非常重要的操作就是构造层次模型图。从结构上看，层次分析法将模型大致分为目标层、准则层和方案层。目标层是你的评价目标，准则层是你的评价指标体系，方案层是多个对比方案。注意，方案层是一定要有多个对象进行比较的，因为层次分析法是基于比较的方法。

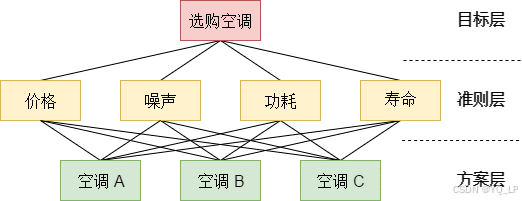
图7.1 使用层次分析法选择空调

两个相邻的层次之间是需要构建成对比较矩阵的。比方说在上图，我们在目标层和准则层之间就需要构建第一层比较矩阵，这个矩阵的大小是行列均为4。矩阵的每一项表示因素i和因素j的相对重要程度。由于对角线上元素都是自己和自己做比较，所以对角线上元素为1。另外，还有一条重要性质：
$$a{}_{ij}a{}_{ji}=1$$
关于这个矩阵的每一项取值多少，若因素i比因素j重要，为了描述重要程度，我们用1~9中间的整数描述，如表5.2所示。

表5.2 重要性程度取值

取值	1	2	3	4	5	6	7	8	9
相对重要程度	同等重要	介于1、3之间	相对重要一些	介于3、5之间	相对比较重要	介于5、7之间	相比明显重要	介于7、9之间	相比非常重要

表5.2中描述的重要性是因素i比因素j重要的情况下描述的。如果是因素j比因素i重要，由式（5.2）得到的“相对不重要程度”那就用1~9的倒数描述即可。这个比较矩阵每一项的确定具有较强的主观性，因为究竟二者重要程度是比较重要还是非常重要也是不同的人可能有不同的理解，但总体来讲是奏效的。

注意：通常来说，对重要性的取值都是取奇数，也就是1、3、5、7、9，偶数是当你不太确定，也就是认为介于两个奇数程度之间时再取偶数。

除了准则层外，方案层也需要构建成对比较矩阵。但不同的是，假如有m个准则n个样本，需要构建的矩阵数量为m，矩阵大小为(n,n)。每个成对比较矩阵是需要我们自己手动确定的。在人工商定了这些成对比较矩阵后，接下来的操作是对每个成对比较矩阵进行一致性检验。在前面我们已经知道如何对矩阵进行特征值分解，那么对于成对比较矩阵可以很容易地计算出它最大的特征值及其对应的特征向量。那么，定义CI值：
$$CI=\frac{\lambda {}_{max}-n}{n-1}$$
这里n取4的话很容易计算出CI值为0.0145。而除了CI，还有一个RI值（随机一致性指标），在不同的n的取值下RI值也不同。这个值是通过大量随机实验得到的统计规律，数值可以查表获得，将RI表列在表5.4中。

表5.4 RI*取值

n	1	2	3	4	5	6	7
RI	0	0	0.52	0.89	1.12	1.26	1.32
n	8	9	10	11	12	13	14
RI	1.41	1.46	1.49	1.52	1.54	1.56	1.58

得到RI和CI后，计算CI和RI的比值也就是CR。查表计算可以得到这个矩阵的CR值为0.0161。通常来说，当CR值超过0.1时，就可以认为这个矩阵是不合理的，需要被修改、被调整。这里由于没有超过这个阈值，所以可以认为这个比较矩阵通过了一致性检验。于是，剩下的过程便可以如法炮制，计算出准则层到方案层的4个矩阵了。

得到一致性检验结果后，还需要对最大特征值对应的特征向量进行归一化得到权重向量。归一化的方法为将特征向量除以该向量所有元素之和：
$$x{}_i=\frac{x{}_i}{\sum _{i-1}^{n}x{}_i}$$
最终可以得到每个指标的权重，以及每个样本在不同指标上的归一化得分。通过加权折算就可以得到评价的最终分数。

7.2 熵权分析法

熵权法是一种客观赋权方法，基于信息论的理论基础，根据各指标的数据的分散程度，利用信息熵计算并修正得到各指标的熵权，较为客观。相对而言这种数据驱动的方法就回避了上面主观性因素造成的重复修正的影响。

7.2.1 熵权分析法的原理

在上一节例7.1中，我们发现一个现象：衡量好坏的标准因指标而异。由于指标的多样性，有些指标越大越好，如成绩；有些越小越好，如房贷；有些在特定区间过高或过低都不佳，如血压；还有些存在最优值，偏差越大越差。若模型未经数据预处理直接计算，可能出现问题。因此，第一步是指标正向化。它涉及将原本的负向指标转为正向指标，例如将死亡率转为生存率、故障率转为可靠度。通过正向化，目标或结果的达成情况更直观，提高指标的可解释性和可操作性。

• 对于极大型指标：指标越大越好，不需要正向化。只需要通过min-max规约或Z-score规约进行规约即可。

• 对于极小型指标：此类指标越小越好。它的正向化方式比较简单，可以取相反数；如果指标全部为正数，也可以取其倒数。

• 对于区间型指标：它的规约方法遵循下面的式子。

  KaTeX parse error: Unknown column alignment: * at position 58: …{\begin{array}{*̲{20}{l}}{1-\fra…

• 对于中值型指标：它的正向化操作为

$$x{}_{new}=1-\frac{\left|x-x{}_{best}\right|}{max\left(\left|x-x{}_{best}\right|\right)}$$

在进行指标正向化以后，所有的指标全部被变换为越大越好。而为了进一步消除量纲这些的影响，需要进一步进行min-max规约化或z-score规约化消除量纲差异。

熵权法的主要计算步骤如下。

（1）构建m个事物n个评价指标的判断矩阵$R(i=1,2,3,\dots ,n；j=1,2,\dots ,m)$。

（2）将判断矩阵进行归一化处理，得到新的归一化判断矩阵$B$。
$$B=\frac{X-min\left(X\right)}{max(X)-min\left(X\right)}$$
（3）熵权法可利用信息熵计算出各指标的权重，从而为多指标评价提供依据。根据信息论中对熵的定义，熵值$e$的计算如下。
$$e{}_j=\frac{\sum _{i=1}^{n}p{}_{ij}lnp{}_{ij}}{lnn}$$
其中$p$为离散属性中每个类取值的占比。通过式(5.8)的熵值，可以评价不同指标的离散程度，一般情况下，信息熵越小，离散程度越大，因子对综合评价的权重就越大。

（4）计算权重系数，式子(5.9)中代表对于某一个属性$j$，第$i$类占样本的比例。$n$为属性$j$的取值数量。所以，权重系数$w$定义为
$$w{}_j=\frac{1-e{}_j}{\sum _{i=1}^m\left(1-e{}_j\right)}$$

注意：熵权法是一个数据驱动过程，一定要保证有一定数据量并且做了正向化。

7.3 TOPSIS分析法

TOPSIS评价法是有限方案多目标决策分析中常用的一种科学方法，其基本思想为，对原始决策方案进行归一化，然后找出最优方案和最劣方案，对每一个决策计算其到最优方案和最劣方案的欧几里得距离，然后再计算相似度。若方案与最优方案相似度越高则越优先。

7.3.1 一般的TOPSIS分析法

中国有句古话，叫做“近朱者赤近墨者黑”。我们要比较各个方案的好坏，但是每个方案都有很多不同的指标，比如经济、环境、社会等等。如果我们直接比较这些指标，可能会很复杂，而且也容易受到不同指标单位和量纲的影响。层次分析法里面我们用成对比较矩阵主观地消除量纲影响，熵权法里面我们用熵值和正向化消除了量纲影响，还有什么办法嘞？在TOPSIS分析法中，我们通过计算每个方案离理想解和负理想解的距离来判断优劣。理想解是最佳方案，各项指标最优；负理想解是最差方案，各项指标最差。这种方法就像“近朱者赤近墨者黑”，离最好的方案越近，表现就越优秀，离最差的方案越远，表现就越差。简化多个指标问题为距离问题，如图所示。

对于距离，有多种方式可以衡量它。包括最常用的欧几里得距离、曼哈顿距离、余弦距离等多种计算方式，它们的计算方法如下：
$$Manhaton(x,y)=\sum _{i=1}^n\left|x{}_i-y{}_i\right|$$