运筹说 第117期｜论文速读之基于M/M/c排队模型的多门越库配送环境下车辆路径问题

前几期的推送已经讲解了排队论的基本知识、数学模型和相关算法，相信大家对排队论已经有了充分的了解，这期小编将带大家一起来读一篇基于M/M/c排队模型的多门越库配送环境下车辆路径问题的文章。

1.文章信息

题目：An M/M/c queue model for vehicle routing problem in multi-door

cross-docking environments

作者：Asefeh Hasani Goodarzi, Eleen Diabat , Armin Jabbarzadeh，Marc Paquet

来源：Computers and Operations Research

出版信息：Volume 138, February 2022, 105513

网址：https://doi.org/10.1016/j.cor.2021.105513

2.文章导读

越库配送作为一种高效的物流解决方案，在全球范围内广泛应用于众多市场领域的众多行业。越库配送是指货物送达仓库后，卸载、收货、分类、重组后直接装载到出库承运车上送达目的地，而无需像传统的库存管理那样存储在仓库中，以减少对仓库存储的需求，加快货物在供应链中的移动。在本文中，产品由进站卡车从不同的产地收集，到配送中心后卸下，与其他产品重新整合，然后在当天或第二天装上出站卡车。这个过程中，车辆在配送中心的等待时间是关键影响因素，如果等待时间过长会延长产品的交付时间，同时增加滞留费用。因此，为了最小化交付时间与滞留费用，需要考虑进站卡车的路径优化问题，这种把越库配送与车辆路径问题相结合，以有效地满足一系列运输需求的问题，被称为带越库配送的车辆路径问题（Vehicle Routing Problem with cross-docking，VRPCD）。此外，在越库配送中由于不同配件需要在配送中心组合后再出库，装载有某一配件的卡车如果没有同时到达配送中心，则会造成组合时间的延迟。此前的研究中只了考虑卡车同时到达的情形，但由于卡车同时到达造成的拥堵，同样会增加时间成本。因此，本文权衡了卡车的同时到达和允许排队的队列长度，放宽了卡车同时到达的约束，假设卡车会在不同的时间段内到达，在此基础上研究配送中心入库门处卡车的排队问题，以及启动取货流程的车辆调度方案。

3.摘要

在越库配送中，入库门资源有限且货车到达时间不确定，不可避免地导致排队问题。码头车辆排队时间较长会降低服务质量，并且会导致配送中心的经济成本增加。因此，本文研究了基于排队论的多门越库配送系统中的车辆路径问题，并且本文的排队模型适用于码头拥堵的情况。本文关注配送中心的入库门，并假设卡车到达配送中心的比率是一个随机变量。此外，配送中心无法同时为所有车辆提供服务，它具有容量约束和服务时间约束等局限性。

本文提出了一个M/M/c排队模型来模拟这种越库配送环境，并确定车辆启动取货过程的调度计划。在所提出的多通道排队系统中，货车到达配送中心的流程可以看作泊松过程，从而得到一个非线性的数学公式来优化问题，然后将模型线性化。为了解决该问题的计算复杂性，本文开发了一种新的遗传算法（GA）来获得问题的近最优解，并将其与优化软件GAMS的解进行了验证；然后对模型的不同参数进行敏感性分析，研究其对队列中车辆运输成本和等待成本的影响。结果表明，在该问题中考虑排队方法，能够显著降低队列中入库卡车的平均等待时间。

4.主要内容

4.1问题描述

本文的研究重点是越库配送中的入站调度问题，主要关注配送中心入库门处卡车的排队问题以及启动取货流程的车辆调度方案。研究的目标是通过最小化网络运输成本（即路线行驶成本与车辆运行成本之和）和排队等待的预期成本来优化系统。本文假设了一个多入库门的越库配送系统，并采用了M/M/c（c>1）排队模型。在这个系统中，入库门被视为排队系统中的处理机（服务器），越库配送操作从第一辆卡车被引导到一个空闲的门开始，直到最后一辆卡车离开其指定的门结束。入库门的数量限制为给定的数c，其中c为正整数，考虑到卡车的数量通常会超过入库门的数量，假设卡车的到达过程和服务时间分别遵循泊松分布和指数分布，且卡车的容量不统一。作者建立了一个混合整数非线性规划（MINLP）模型来描述该问题，并采用遗传算法进行求解。为了验证求解算法的性能，通过具体的实验比较了优化软件GAMS和遗传算法的求解时间，结果显示遗传算法的计算时间更短。

4.2数学模型

本文建立了一个混合整数非线性规划（MINLP）模型，旨在确定使得卡车的出行成本、运营成本和平均排队等待成本最小的最佳路线。该模型考虑了车辆容量、整个过程的时间范围以及配送中心发生超长排队的概率等各种约束条件。

​

 图1 MINLP模型

 模型的解释如下：目标函数（1）使车辆的总运输成本和运行成本以及平均排队等待时间成本最小。约束（2）和（3）将配送中心作为所有路由的初始和最后节点。约束（4）保证了流量守恒，并规定车辆进入一个节点之后必须离开。约束（5）和（6）要求每个节点分别只有一辆车进入和离开，这意味着不能进行拆分服务。约束（7）表示可用车辆的最大数量。取货和发货过程中所装载的商品（船上产品）数量分别用约束（8）和约束（9）表示。约束（10）规定每辆车的载货总量不能大于其承载能力。约束（11）设置了每个取货或送货节点允许启动服务的时间。约束（12）规定了车辆完成该过程的时间范围。取货过程结束后，每辆车在约束（13）所表示的时间进入配送中心。在约束（14）中，确定每辆出站车辆取货过程的开始时间。概率约束（15）对超过b辆卡车在交叉码头排队等候的概率施加了一个阈值θ。约束（16）使用两个变量计算队列中车辆的平均等待时间：平均队列长度Lq 和车辆到达率λ 。约束（17）和（18）防止了拾取和交付过程的混合。最后，约束（19）定义了变量的性质。

​

 图2 MINLP模型

约束（20）将概率方程（15）转换为其等效的确定性和线性约束。Ps是有c个服务器的系统中有s个现有客户（相当于卡车）的稳态概率。式（21）和式（22）分别为服务率和到达率。约束（23）为配送中心卡车数目为0的概率P0 。公式（24）表示系统中有n辆卡车的概率。将约束（20）右侧代入已知的c、λ 和µ的值，转化为式（25）。

​

 图3 MINLP模型

利用上述方程中已知的c、λ 和µ的值，计算出每个s的Ps值，将式（20）改写为式（26）。式（27）表示两个连续到达卡车之间的时间。考虑到排队约束，到达率应受交叉码头的最大到达率（λmax ）的限制，同一时间间隔内到达的卡车总数应以公式（28）中规定的λmax 为界。约束（29）为队列中车辆的平均等待时间。为了线性化（27），将方程重新表述为式（30）-（34）。由于存在二元变量，将（28）改写为（35）。式（36）通过对数函数将式（29）中的幂函数线性化。

4.3构建算法

本文为求得最优解，提出了一种新的遗传算法，新算法相比于原始算法在生成初始种群步骤进行了改进。首先，生成一个巨型巡回染色体，其中形成一个包含所有节点的随机巡回路线，然后根据生成的路线中随机选择的卡车的订单，在考虑容量和时间限制的情况下，为它们分配节点。使用维度为|V|*|N|的矩阵创建一个可行的解决方案，其中|V|是可用卡车的数量，|N|等于节点的数量（包括配送中心）。然后进行适应度评估，本研究中使用的适应度函数是每条路线的总成本加上在定义矩阵（fVRP（h））中评估的应用卡车的运营成本。然后进行交叉和变异，本文中的交叉点是随机选择的，变异选择了三种方式，分别是：同一路径上的成对交换（反转）、路径消除和组合、交换。最后，停止条件为达到规定的迭代次数，本文小型和大型问题实例的终止条件分别设置为300和500。

4.4实验

本文通过数值实验评估所提出的公式和求解方法的可行性，选择了中东一家汽车制造公司的10家供应商进行实验，通过优化软件GAMS（22.9版）编码并解决该问题。

卡车从配送中心可以采用同时派出或者可变的时间派出这两种方案，本文通过实验验证了哪种方案的平均等待时间更短。共进行了三次实验，其中从配送中心调度货车m到开始取货过程的时间是模型的输入，记为fm 第一次实验假设fm 服从泊松分布，平均为2辆/小时，并取消了最大到达率的约束，得出卡车排队的平均等待时间为20.33min。第二次分析了当所有卡车同时调出发情况下排队长度和等待时间，即fm 都为0，也取消了最大到达率的约束，平均等待时间为57.33min，比第一种状态中货车异构和已知调度时间的平均等待时间（20.33min）高出182%。第三次实验分析了所有卡车调度时间都可变的情况下队列长度和等待时间，所有的fm 都可变，同时也施加条件λ ≤λmax ，设置λmax 为0.84，即为保证至少80%的时间内排队长度（b）等于或小于2，得出排队的平均等待时间为4.5分钟，比第一次平均等待时间（20.33分钟）减少了351.8%。因此，说明所有货车的调度时间可变的情况下的等待时间最短，该结论也证明了作者提出的“不必同时调度卡车”的创新点是有效果的。

为了研究不同参数对问题的各种性能指标的影响，本文生成了四个小规模实验和三个大规模实验，小规模指的是|N|=5、10和15的测试问题，大规模实验是指|N|=20、40和80的测试问题。

然后，通过小型实验验证求解方法的性能。在c、b和θ不同参数下运行四个测试问题，分别用GAMS和新提出的遗传算法进行求解。问题1设置节点数为10，取货节点数为6，对问题一的测试结果如图4，遗传算法的结果如图5。可以看出，遗传算法能够显著减少运行时间。并且，GAMS方法的结果发现λ 对λmax 的变化不敏感，在所有情况下都保持为0.29。并且在所有情况下，运输路线和运输成本都是相同的，而排队成本则根据入库门的数量略有变化。遗传算法的结果表示，增大λmax 的界，λ 的值也会增大，总运输成本与精确方法值相同，而队列中卡车的等待成本不同。问题2将λ 的值稍微增大，其余条件不变，结果发现参数变化趋势与测试问题一相似。

​

图4 问题一的GAMS结果

​

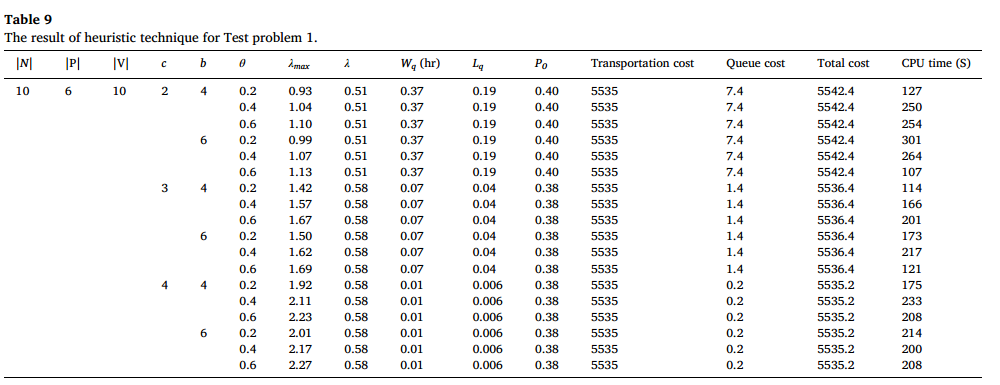
图5 问题1的遗传算法结果

测试问题3设计了总节点数为15和9个拾取节点，GAMS方法结果如图6所示，通过增加入库门的数量，排队成本显著降低，将c=2增加到c=3，排队成本提高87%，将c从2改变到4，排队成本降低约98%。遗传算法的结果如图7所示，比较表12和表13可以发现，λ 值的小幅增加可能会显著提高排队成本。

​

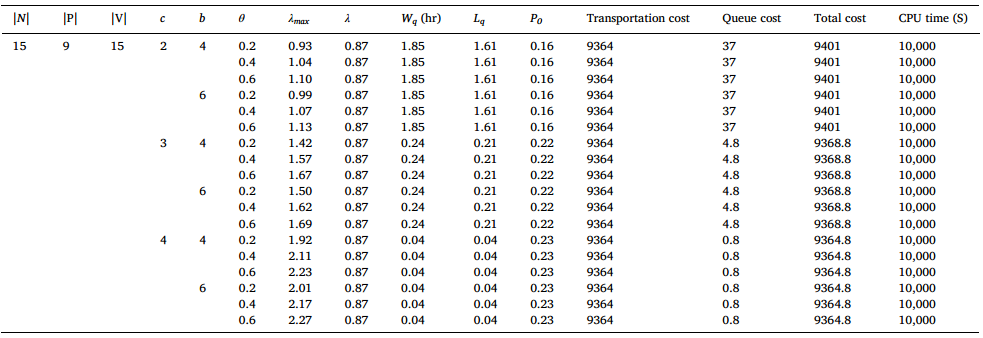
图6 问题3的GAMS结果

​

图7 问题3的遗传算法结果

问题4的节点数目与问题三相同，并调整λ 的值，使其与最大到达率相等，一直到允许的最大阈值1.67，该问题只通过GAMS求解，结果如图8所示，发现随着到达率的增大，到达取货节点的路线会形成更经济的路线，运输成本降低。

​

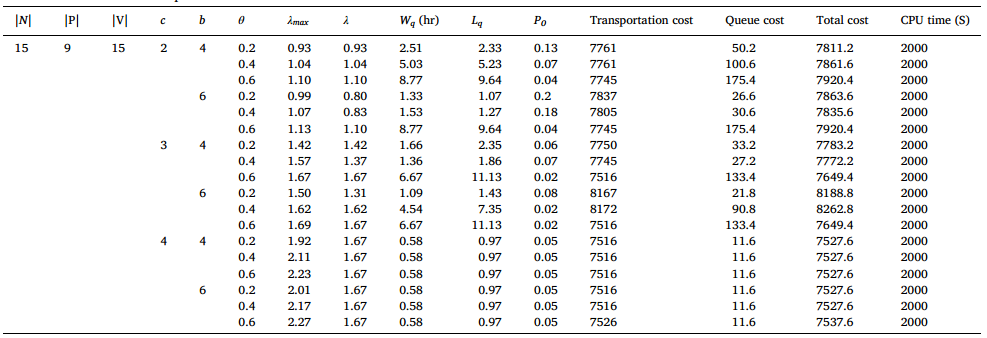
图8 问题4的GAMS结果

此外，本文为了对参数进行敏感性分析，还进行了|N|=20、40和80大规模实验。由于软件GAMS无法在限定时间内求解模型，因此该部分只采用遗传算法进行求解，探究在大型问题中，θ、b、c、V对目标函数值的影响。图9-图11显示了|N|=20、40和80，b=4或6，θ=0.2、0.4和0.6情况下目标函数值的变化趋势。对于大规模的情况，θ增大时，运输成本降低，同时，增加入库门的数量可以导致更高的λmax ，从而使路线更具成本效益。在前两种情况下增加最大排队长度b也可以增加λmax ，从而降低运输成本。然而，在|N|=80的测试问题中，情况并非如此，这可能是因为GA找到了接近最优的解。

​

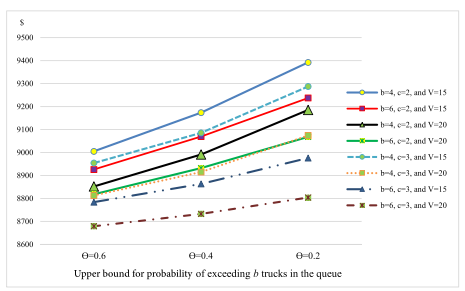
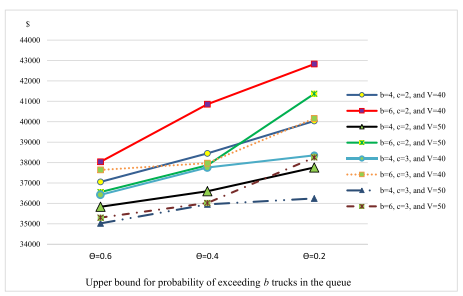
图9 N=20时目标函数值      图10 N=40时目标函数值    图11 N=80时目标函数值

5结论

本研究以提高越库配送效率为出发点，考虑了基于排队论的多门越库配送系统中的车辆路径问题。在拥堵情况下，一辆卡车在取货后到达配送中心时，可能没有足够的资源（入库门）来同时卸载所有停靠的卡车，导致排队问题。作者提出了一个非线性数学模型来描述这一问题，创新之处在于并非所有卡车都必须同时调度，而是通过变量fm 确定每辆卡车的调度时间。实验证明，在卡车调度时间可变的情况下，排队等待时间显著减少，表明一些公司可以根据货车到达速度和交叉码头服务速度晚些时候启动取货流程。为了求解该模型，提出了一种新的遗传算法，并进行了参数敏感性分析和具体实验验证。数值实验证明了所提出的公式和求解方法的有效性，并发现增加入库门数量可以提高最大到达率，使得路线更具成本效益，增加队列长度概率的可接受阈值θ则可以降低运输成本。

6贡献

1、本文考虑了配送中心派出卡车到供应商节点取货的最佳开始时间，改进了以往都为零时间的假设，使得配送中心能够更好地安排卡车从供应商工厂取货。

2、本文同时考虑了VRP、越库配送和排队理论，并考虑可能的排队长度、车辆最大到站率、平衡条件和队列中车辆的平均等待时间，填补了这一研究空白。

7展望

在未来的研究中，可以考虑采用分离式车辆路径问题（VRP），这将允许供应商和客户可以灵活地供应或接收多批产品，并且每个节点可以被访问多次，从而减少所需的卡车数量。此外，该模型可用于战略或战术层面，确定入库门的数量，以优化卡车在配送中心的等待时间和排队长度。