重读初中数学课本之六年级下册

算是放松下自己，看看在初中课本上还能学学到那些新东西，正所谓“温故而知新”嘛。

采用的是鲁教版图书，图片一部分摘录于书中，部分为网上。

基本平面图形

角

引起关于时钟中对时钟和分针的思考

时针一分钟旋转0.5°，分针一分钟旋转6°

三角板的妙用

15n 都是15°的倍数

多边形中三角形的个数

三角形的个数：多边形-2（在该顶点相交的两条线段去除)

线段

四边形内一点到顶点的最短距离

由这个题我又想了想那三角形呢？

开始看的是B站一up主讲的三角形的四心，发现都不是。后来一查，原来有名字呐，费马点。

拓展：三角形的四心及费马点

重心

即三条中线的交点

证明方法：相似三角形和中位线

在向量中的应用

垂心

即三角形三边高的交点

利用向量的乘积来证明，在向量的数量积里有应用。

外心

即外接圆的圆心，三边垂直平分线的交点

性质：到三个顶点的距离相等。

内心

即内切圆的圆心，三个角平分线的交点。

对直角三角形来说

对一般三角形来说

单位向量

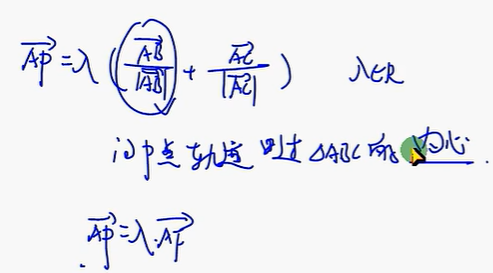
费马点

在物理学中的应用：重力势能最小

三角形的四心问题详解

整式的除法

数形结合法理解积的乘方

积的乘方等于把积的每一个因式分别乘方，然后将所得的ࣦ积相乘.

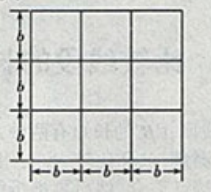
将2和5的次方化成同指数

零指数幂和负整数指数幂

多项式与多项式相乘的拆解引例

通过几何图形边与边的关系、边与面积的关系引入了二次函数的最值问题

平方差公式的几何表示形式

平方差公式的简单应用

完全平方公式的几何表示形式

这是相加时候的图形

这是相减时候的图形

完全平方公式的使用

和二项式和杨辉三角联系

关于杨辉三角我们不难发现每一行的首末都是1，并且下一行的数比上一行多1。中间各数都写在上一行两数的中间，且等于它们的和。

由这个问题想到了几个平均数

该题的答案是不等，相差1/4

（需要问一下自己，为什么不等，差值有什么特殊性）

其实就是用到了勾股定理证明算数平均数和平方平均数的大小

射影定理证明算数平均数、几何平均数、调和平均数的大小

这里看了B站的视频，给出了其证明。

其原理用到了射影定理，在一个圆中给予证明。

射影定理和几种平均数比较思路

原理：相似三角形的比值

小时候因为那些“偷懒”代数计算出来忽略了原理证明，真是一大“损失“呐。

未完待续的代码编译

任意一个不是有完全相同数字的组成的四位数，如果对它们的每位数字重新排序，组成一个最大的数各一个最小的数，然后用最大数减去最小数，差不够四位数时补零，类推下去，最后将变成一个固定的数：6174，这就是卡布列克常数。

//类似水仙花数 

//判断数的位数（是不是可以根据strlen判断长度） 
//创建一个数组  
//申请动态内存组成数组（2倍该数的大小） 
//对数进行正反排序 
//然后根据根据位权进行相乘得到这两个数
//做差
//重复上面的步骤

#include <stdio.h>
#include <string.h>

int main()
{
    
    return 0;
} 

这里只写了思路，未完待续。

数学归纳思想

本质：数x乘以1001x 即1000x + x

相交线与平行线

同角或等角的余角相等，同角或等角的补角相等（和等量代换类似）

同位角只是位置相同，相不相等另说，内错角和同旁内角同理

坐地日行八万里和内错角

运用了两条直线被第三条直线所截，内错角相等。单位角度测算地球周长。

两刀剪出来的正方形

数据的收集与整理

这里的“人数”表示优、中、良的频繁程度，因此也称为频数 。 数据越多，分的组数也就多. 当数据在 100 以内时，通常按照数据的多少，分成5至12 组.

变量之间的关系

三种方法表示变量之间的关系

表格表示法，表达式表示法，图像表示法

小车下滑引出变量之间的概念

支撑物高度 h 和小车下滑时间 t 都在变化，它们都是变量 （variable). 其中 t 随 h 的变化而变化，h 是自变量（independent variable）,t是因变量（depentent variable). 在这一变化过程中，小车下滑的距离（木板长度）一直没有变化. 像这种 在变化过程中数值始终不变叫做常量(constant).