蓝桥杯备赛——算法入门初阶（2）

目录

内容简介

1.差分

1.1一维差分

1.2二维差分

2.双指针（滑动窗口）

---

内容简介

上一篇文章我们已经了解了模拟，高精度，枚举，前缀和算法，之后我们将继续学习一些入门算法。

1.差分

1.1一维差分

差分与我们之前讲到的前缀和类似，都是通过预处理数据，从而可以快速地找到我们想要的值，从而优化时间复杂度。简单来看，差分和前缀和像是一对逆运算

【模板】差分

我们可以通过这道模版题来理解一下差分算法的写法，以及它的作用。

我们通过这个图可以看出，差分数组的f[i]的值就是原数组a[i]-a[i-1]的值，也就是原数组当前项与前一项的差。

我们现在明白差分数组的写法，那差分数组到底在什么时候使用呢？当题目要求我们在区间[left,right]区间上加减上某个数的时候，我们可以使用差分快速完成。

即：f[left] += x , f[right+1] -= x;

完成加减操作之后，因为差分与前缀和是逆运算，我们只需要再使用前缀和算法对差分数组求前缀和，即可把差分数组还原成原数组。

#include <iostream>
using namespace std;
const int N=1e5+10;

int n=10;
int a[N];//原数组 
int f[N];//差分数组 

int main()
{
    cout<<"原数组:";
	for(int i=1;i<=n;i++){
		a[i]=i; 
	}
	//打印原数组 
	for(int i=1;i<=n;i++) cout<<a[i]<<" ";	
	cout<<endl;
	
	//建立差分数组
	for(int i=1;i<=n;i++){
		f[i]=a[i]-a[i-1];
	} 
	//在[left,right]区间加上x
	int left,right,x;
	cout<<"输入区间范围和加减值";
	cin>>left>>right>>x;
	f[left]+=x;f[right+1]-=x;
	
	//还原数组并打印 
	cout<<"更改后的数组：";
	for(int i=1;i<=n;i++){
		f[i]=f[i]+f[i-1];
		cout<<f[i]<<" "; 
	} 

	return 0;
}

1.2二维差分

二维差分就是在基于二维数组进行差分，一维数组中我们要求改变一段区间的值，在二维差分中，我们要求在一个矩阵中修改值。

【模板】二维差分

与一维差分的步骤类似，先建立根据原数组建立差分数组，在差分数组进行加减数值，最后利用二维前缀和还原数组。

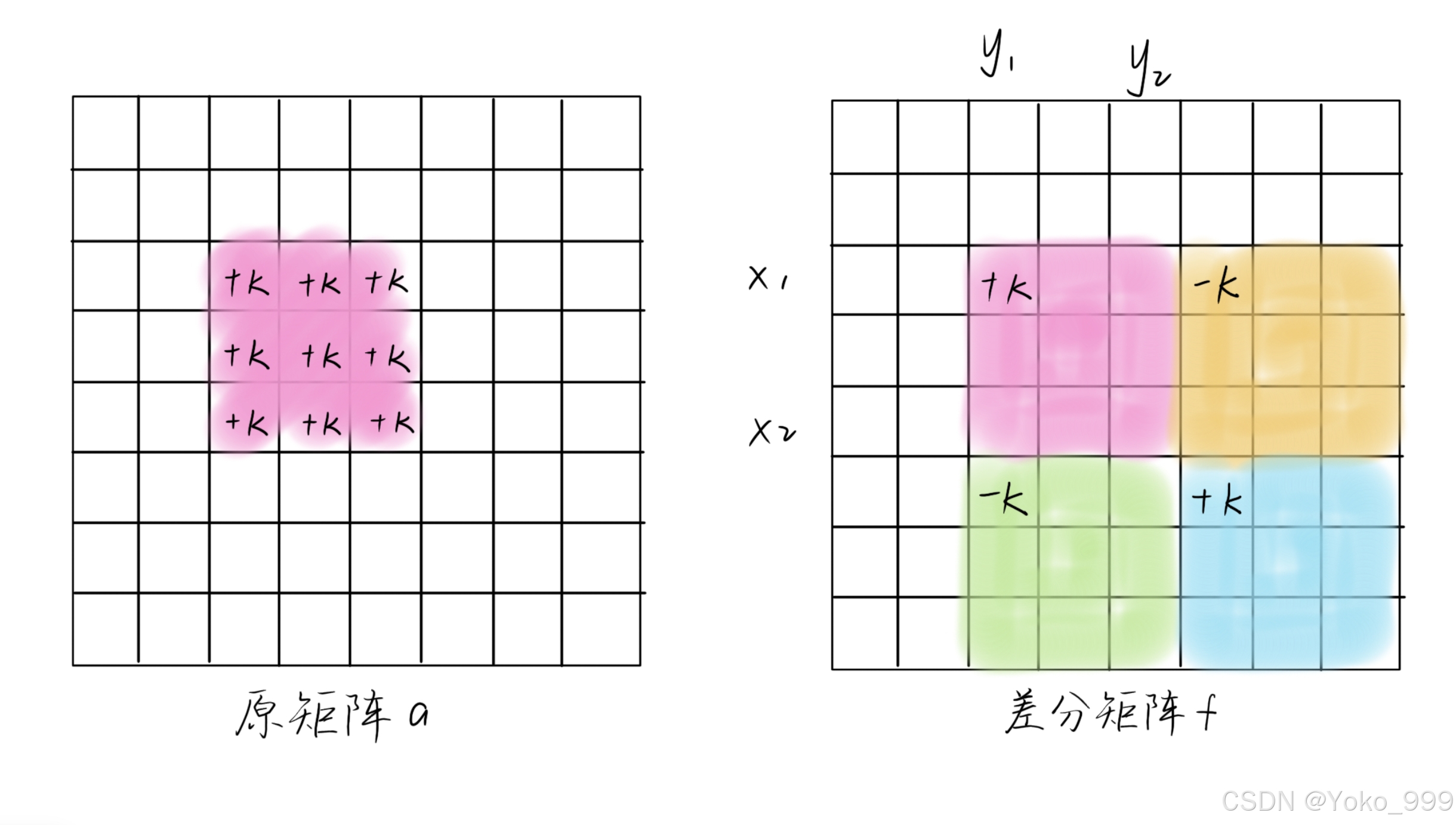我们需要在（x1,y1,x2,y2）内加上k，如果在差分数组f的（x1,y1）处加k，在后期求前缀和的时候，会使四种颜色的区域都加上k，而我们只想要粉色区域+k。此时我们在黄色区域左上角-k， 就可以消除黄色区域和蓝色区域-k，在绿色区域左上角-k，同理也会在绿色和蓝色区域-k，而蓝色区域被两次-k，最后在蓝色区域左上角+k，就可以消除误差。

#include <iostream>
using namespace std;

typedef long long LL;
const int N=1010;
int n,m,q;
LL f[N][N];

void insert(int x1,int y1,int x2,int y2,int k){
	f[x1][y1]+=k;
	f[x2+1][y1]-=k;
	f[x1][y2+1]-=k;
	f[x2+1][y2+1]+=k;
}

int main(){
	cin>>n>>m>>q;
	//建立差分数组 
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			LL x;
			cin>>x;
			insert(i,j,i,j,x);
		}
	}
	while(q--){
		LL x1,y1,x2,y2,k;
		cin>>x1>>y1>>x2>>y2>>k;
		insert(x1,y1,x2,y2,k);
	}
	
	//利用二维前缀和还原数组
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			f[i][j]=f[i][j-1]+f[i-1][j]-f[i-1][j-1]+f[i][j];
			cout<<f[i][j]<<" ";
		}
		cout<<endl;
	} 
	
	
	return 0;
}

2.双指针（滑动窗口）

这里的双指针不是简单的两个指针，使用循环达到题目的要求。这里的指针有这一个很重要的性质：“不回退”，左指针和右指针是一直往一个方向移动的，不需要回退。

我们在拿到题目的时候，往往会在暴力枚举的解法靠，在枚举的过程中，我们发现左右指针都满足不回退的性质，此时我们就可以使用滑动窗口优化算法。

UVA11572 唯一的雪花 Unique Snowflakes - 洛谷

#include <iostream>
#include <unordered_map>

using namespace std;
const int N=1e6+10;
int T; 
int n;
int a[N];

int main()
{
	cin>>T;
	while(T--){
		cin>>n;
		for(int i=1;i<=n;i++){
			cin>>a[i];
		}
		int left=1,right=1,ret=0;
		unordered_map <int,int> st;
		while(right<=n){
			//进窗口 
			st[a[right]]++;
			//判断不合法 
			while(st[a[right]]>1){
				st[a[left]]--;
				left++;
			} 
			//窗口合法后更新
			ret=max(ret,right-left+1); 
			
			right++;
		}
		cout<<ret<<endl;
	}
	return 0;
}

left指向当前包裹的第一片雪花，right++，如果a[right]的值在当前包裹没出现过，那么就把他存入当前包裹，如果出现了，那就让left++，直到a[right]在包裹里只出现一次。窗口每次合法之后更新包裹的个数。