NJU-高级算法-牛繁殖问题

Description

Cows in the FooLand city are interesting animals. One of their specialties is related to producing offsprings. A cow in FooLand produces its first calve (female calf) at the age of two years and proceeds to produce other calves (one female calf a year).

Now the farmer Harold wants to know how many animals would he have at the end of N years, if we assume that none of the calves die, given that initially, he has only one female calf?

explanation:At the end of 1 year, he will have only 1 cow, at the end of 2 years he will have 2 animals (one parent cow C1 and other baby calf B1 which is the offspring of cow C1).At the end of 3 years, he will have 3 animals (one parent cow C1 and 2 female calves B1 and B2, C1 is the parent of B1 and B2).At the end of 4 years, he will have 5 animals (one parent cow C1, 3 offsprings of C1 i.e. B1, B2, B3 and one offspring of B1).

Input

The first line contains a single integer T denoting the number of test cases. Each line of the test case contains a single integer N as described in the problem.

Output

For each test case print in new line the number of animals expected at the end of N years modulo 10^9 + 7.

Sample Input 1 

2
2
4

Sample Output 1

2
5

思路

题目大意：第0年有1只母牛A；第1年有1只母牛A；第2年2只母牛A，B（A生的）；第3年3只母牛A，B，C（A生的）；第4年5只母牛A，B，C，D（A生的），E（B生的）...

若记第N年末有F(N)只母牛，则有递推关系F(N) = F(N-1) + F(N-2)，其中F(N-1)表示前一年所有的牛（因为牛不会死亡，所有牛都存活到今年），F(N-2)表示两年前出生的牛今年开始具备繁殖能力，且每头生1只牛。

可以看到这其实是一个斐波那契数列问题。

1.简单的递归

n=0或n=1时，F(n) = 1

n>1时，F(n) = F(n-1) + F(n-2)

代码：

import java.util.Scanner;

public class Main {
    
    /*
     *z递归法
     *z第一年末：一头牛（A)
     *z第二年末：两头牛（A，B(A生了B)）
     *z第三年末：三头牛（A，B，C(A生了C)）
     *z第四年末：五头牛（A，B，C，D（A生了D），E（B生了E））
     *z第五年末：八头牛（A，B，C，D，E，F（A生了F），G（B生了G），H（C生了H））
     *z...
     *z可以总结出结论：
     *T(N) = T(N - 1) + T(N - 2)
     *T(N - 1)表示前一年所有牛的数量，因为第N年时前一年的所有牛都没死
     *T(N - 2)表示第N年时两年前新出生的牛今年开始具备繁殖能力,从而生出的新牛的数量
     * 
     * */
    private static int cal(int n) {
        if(n == 0) {
            return 1;
        } else if(n == 1) {
            return 1;
        } else {
            return cal(n - 1) + cal(n - 2);
        }
    }

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int cases = Integer.parseInt(sc.nextLine());
		for(int turn = 0; turn < cases; turn++) {
		    int n = Integer.parseInt(sc.nextLine());
		    int res = cal(n);
		    
		    System.out.println(res);
		}
		sc.close();
	}
}

但用递归超时，递归是时间复杂度为O(n)的解法，斐波那契数列还存在一种O(logn)的解法

2.动态规划

参考了：Fibonacci 数列O(logn)解法

递归慢的原因在于重复计算，导致有很多不必要的开销。

采用动态规划，所有值只需要进行一次计算。

斐波那契数列an(n ≥ 0)，可以通过矩阵乘法的方式进行递推：

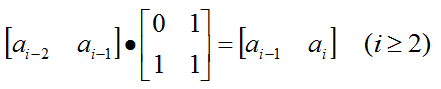
进而可以得到：

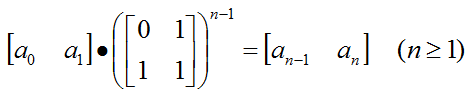
而对于求幂运算，暴力累乘时间复杂度为O(n)，但可以通过递归进行优化：

a^n = (a^(n/2))^2 * a^(n%2)

这里的n/2是取整，如5/2=2。这样就可以实现相当于二分的效果，时间复杂度为O(logn)。

代码：

import java.util.Scanner;

public class Main {
    
    //两个二维矩阵相乘
    private static long[][] multMartix2_2(long[][] m1, long[][] m2) {
        long[][] res = new long[2][2];
        res[0][0] = m1[0][0] * m2[0][0] + m1[0][1] * m2[1][0];
        res[0][1] = m1[0][0] * m2[0][1] + m1[0][1] * m2[1][1];
        res[1][0] = m1[1][0] * m2[0][0] + m1[1][1] * m2[1][0];
        res[1][1] = m1[1][0] * m2[0][1] + m1[1][1] * m2[1][1];
        
        return res;
    }
    
    //1行2列矩阵乘二维矩阵
    private static long[] multMatrix1_2(long[] m1, long[][] m2) {
        long res[] = new long[2];
        res[0] = m1[0] * m2[0][0] + m1[1] * m2[1][0];
        res[1] = m1[0] * m2[0][1] + m1[1] * m2[1][1];
        
        return res;
    }
    
    //二维矩阵的幂
    private static long[][] powMatrix2_2(long[][] m, long n){
        long[][] res = new long[2][2];
        if(n == 0) {
            res[0][0] = res[1][1] = 1;
            res[0][1] = res[1][0] = 0;
            return res;
        } else if(n == 1) {
            return m;
        } else {
            long[][] half = powMatrix2_2(m, n / 2);
            return multMartix2_2(multMartix2_2(half, half), powMatrix2_2(m, n % 2));
        }
    }
    
    private static long fib(long n) {
        if(n == 0) {
            return 1;
        }
        if(n == 1) {
            return 1;
        }
        //斐波那契数列的递推矩阵为{{0, 1}, {1, 1}}
        long[][] m = {{0, 1}, {1, 1}};
        //斐波那契数列初始两值为1
        long[] m0 = {1, 1};
        long[][] powRes = powMatrix2_2(m, n - 1);
        long[]res =  multMatrix1_2(m0, powRes);
        return res[1];
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int cases = Integer.parseInt(sc.nextLine());
        for(int turn = 0; turn < cases; turn++) {
            long n = Long.parseLong(sc.nextLine());
            long res = fib(n);
            
            System.out.println(res);
        }
        sc.close();
    }
}