7.2 AVL树

最新推荐文章于 2024-05-17 08:01:33 发布

ZXG20000

最新推荐文章于 2024-05-17 08:01:33 发布

阅读量187

点赞数 1

分类专栏：数据结构笔记

本文链接：https://blog.csdn.net/ZXG20000/article/details/114263749

版权

数据结构笔记专栏收录该内容

30 篇文章 3 订阅

订阅专栏

参考博客：https://blog.csdn.net/zfliu96/article/details/88538645
参考博客：https://blog.csdn.net/weixin_41698717/article/details/107613262

本章问题

1.AVL树的基础操作有哪些

操作	功能
zig 旋转-顺时针旋转	实现等价前提下的局部拓扑调整
zag旋转-逆时针旋转	实现等价前提下的局部拓扑调整

注意：在下列图片之中，圆圈表示的节点，矩形表示的子树

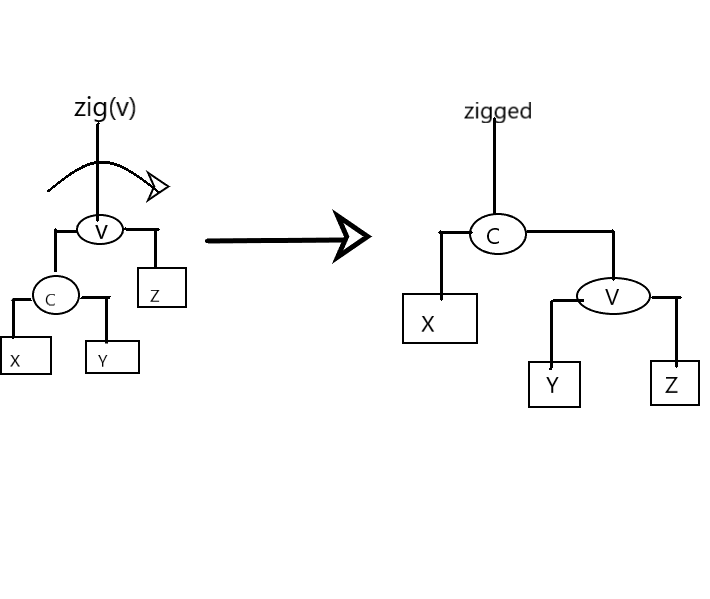
zig旋转 -顺时针

旋转过程描述：将x和v作为c的左子树和右孩子，y和z分别作为v的左右子树

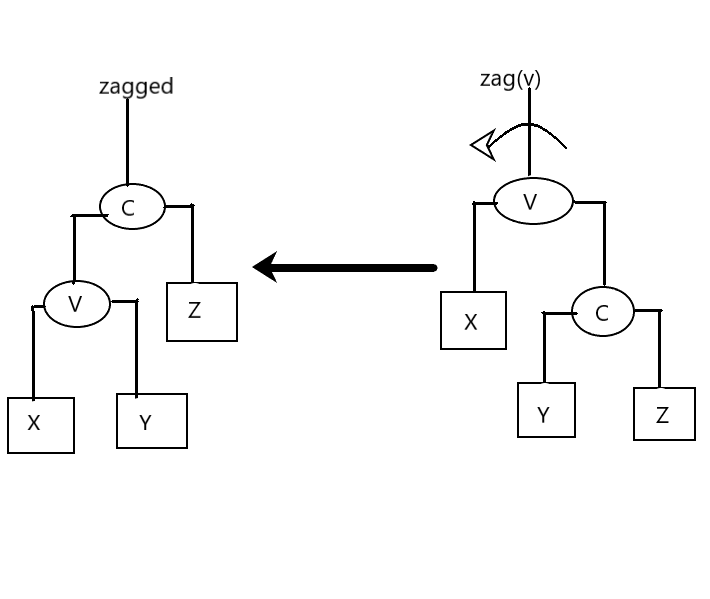
zag旋转-逆时针

旋转过程描述：将v和z作为c的左孩子，右子树，x和y分别为作为v的左,右子树

2.导致AVL树失去平衡的原因有哪些？

参考博客:https://blog.csdn.net/zfliu96/article/details/88538645

2.1、插入结点后失衡

若在插入新的结点 x 之后 AVL 树 T 失去平衡，则失去平衡的结点只可能是 x的祖先，且层次数小于等于 x 的祖父的结点；也就是说失去平衡的结点是从 x 的祖父到根的路径上的结点，但这些结点并不都是失去平衡的结点，有些结点仍然可能是平衡的。
为了修正失衡的现象，可以从结点 x 出发逆行向上，依次检查 x 祖先的平衡因子，找到第一个失衡的祖先结点 g。在从 x 到 g 的路径上，假设 p 为 g 的孩子结点，v 为 p 的孩子结点。根据前面的讨论，结点 p、v 必不为空，p 至少是 x 的父亲，v 至少是 x 本身。
结点 g、p、v 之间的父子关系共有 4 种不同的组合，以下根据这 4 种不同的组合，通过对结点 g、p 的旋转，使这一局部恢复平衡。

(1). p 是 g 的左孩子，且 v 是 p 的左孩子
在这种情况下，必定是由于在 v 的后代中插入了新结点 x 而使得 g 不再平衡。针对这种情况，可以简单的通过结点 g 的单向右旋，即可使得以 g 为根的子树得到平衡。这一过程如下图所示。在这里插入图片描述

当这一局部经过单向右旋调整后，不但失衡的结点 g 重新平衡，而且经过这一调整后，这一局部子树的高度也恢复到插入 x 以前的高度。因此 x 所有其他祖先的平衡因子也都会得到恢复，也就是说，在这种情况下，只需要一次旋转操作，即可使整棵 AVL 树恢复平衡。例如，上图中插入结点 x 之前这一局部子树的高度为 h，经过旋转操作之后，得到平衡的子树高度仍然为 h。
在插入结点 x 之前树是平衡的，此时树的高度为 Ο(log n)，则从 x 出发查找 g 需要花费的时间为 Ο(log n)，而进行平衡所需的一次旋转操作只需 Ο(1)时间，因此整个平衡过程只需Ο(log n)时间。

(2). p 是 g 的右孩子，且 v 是 p 的右孩子
与第一种情况对称，此时，失衡是由于在 g 的右孩子的右子树中插入结点 x 造成的。在这种情况下需要通过结点 g 的单向左旋来完成局部的平衡。这一过程如下图所示。在这里插入图片描述

通过上图不难看出，和单向右旋一样，在旋转之后不但失衡的结点 g 重新平衡，而且子树的高度也恢复到插入 x 以前的高度，因此局部的平衡能使得整棵树得到平衡。这一操作需要的时间与单向右旋相同，也为 Ο(log n)

(3). p 是 g 的左孩子，且 v 是 p 的右孩子
如果是在 p 的左孩子的右子树中插入一个结点，则对应为第三种情况。在这种情况中，要使得局部的失衡重新平衡，那么需要先后进行先左后右的双向旋转：第一次是结点 p 的左旋，第二次是结点 g 的右旋。这一过程如下图所示。在这里插入图片描述
失衡的局部经过双向旋转后，失衡的结点 g 重新平衡，并且子树的高度也恢复到插入结点 x 之前的高度，结点 x 的祖先结点的平衡因子都会恢复。在这种情况下，只需要两次旋转操作就可以使得整棵 AVL 树恢复平衡。同样，为了确定 g 的位置需要 Ο(log n)时间，旋转操作需要 Ο(1)时间，因此，整个双旋操作只需 Ο(log n)时间。

(4). p 是 g 的右孩子，且 v 是 p 的左孩子
第四种情况与第三种情况对称，其平衡调整过程也与第三种情况对称，可以通过先右后左的双向旋转来完成，其中第一次是结点 p 的右旋，第二次是结点 g 的左旋。调整过程如图下图所示。在这里插入图片描述

同样在旋转之后不但失衡的结点 g 重新平衡，而且子树的高度也恢复到插入 x 以前的高度，即局部的平衡能使得整棵树得到平衡。这一操作需要的时间与先左后右双向旋转相同，也为 Ο(log n)

通过以上四种情况的分析，可以得到如下结论：在 AVL 树中插入一个结点后，至多只需要进行两次旋转就可以使之恢复平衡。进一步，由于在 AVL 树中按一般二叉查找树的方法插入结点需要 Ο(log n)时间，旋转需要 Ο(1)时间，则在 AVL 树中结点插入操作可以在 Ο(log n)时间内完成。

2.2、删除结点后失衡

按照通常的二叉查找树删除结点的方法在AVL树中删除结点x之后，如果发生失衡现象，为了重新平衡，同样从x出发逆行向上找到第一个失衡的结点g，通过旋转操作实现AVL树的重新平衡。使得结点g失衡的原因可以看成四种：

（1）. 失衡是由于 g 的左孩子的左子树过高造成的；
（2）. 失衡是由于 g 的右孩子的右子树过高造成的；
（3）. 失衡是由于 g 的左孩子的右子树过高造成的；
（4）. 失衡是由于 g 的右孩子的左子树过高造成的。
这四种情况与插入结点导致失衡的四种情况进行平衡化的旋转方法相同。但是需要注意两个特殊情况：其中之一是失衡可能是由于左孩子的左、右子树同时过高造成的，这种情况如下图所示。从图中可以看出对这种情况的处理可以归为情况 1 或 3 进行处理都是可以的，即图（a）可以通过简单的结点 g 的右旋完成，如图（b）所示；或通过先左后右的双向旋转完成，如图（c）所示。另一种特殊情况与此对称，同样也可以归结为情况 2 或 4处理。
在这里插入图片描述

由于 AVL 树的高度为 Ο(log n)，如此，我们有以下结论：在 AVL 树中删除一个结点后，至多需要 Ο(log n)次旋转即可使之平衡。进一步，由于在 AVL 树中按通常查找树的方法删除结点需要 Ο(log n)时间，平衡调整也需要 Ο(log n)时间，因此，在 AVL 树中删除结点的操作可以在 Ο(log n)时间内完成。

失衡传递
删除结点后，根据失衡结点 g 的四种不同情况进行相应的旋转操作，即可使得局部恢复平衡，但是和插入结点使 AVL 树失衡不同的是，在删除结点的情况下，局部重新平衡不一定会使得 AVL 整体恢复平衡，即会造成失衡的传递。例如在上图所示的情况下，子树在删除结点之前和删除结点之后的高度都为 h+1，此时局部平衡会使 AVL 树整体平衡；然而在有些情况下，删除结点并调整平衡之后，局部子树的高度会降低，如下图所示。在这里插入图片描述

从上图可以看到，在删除结点 x 之前，子树的高度为 h+1，而在删除结点 x 并调整平衡之后，子树的高度为 h，此时由于子树高度下降，会导致某些祖先结点将有可能因此失去平衡。这种由于对局部的重新平衡而造成更上层祖先失衡的情况，称为“失衡传播”。当发生失衡传播时，需要对到根结点路径上的失衡结点依次进行平衡操作，直到根结点为止。

3.在3+4重平衡中怎么判断该进行左旋还是右旋

第1步：判断操作节点v的父节点p是祖父节点g的左右儿子，是左儿子进行zig准备，是右儿子进行zag准备
第2步：若第一步判定为左儿子
第3步：判断操作节点v是父节点p的左右儿子，若是左儿子，进行zig-zig，若是右儿子，进行zig-zag
第4步: 若第一步判定为右儿子
第5步：判断操作节点v是父节点p的左右儿子，若是右儿子，进行zag-zag，若是左儿子，进行zag-zig

connect3+4 连接

//3+4连接
template <typename T> BinNodePosi(T) BST<T> :: connect34(
    BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c,
    BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3
){
    a->lc = T0; if( T0 ) T0->parent = a;
    a->rc = T1; if( T1 ) T1->parent = a; BinTree<T>::updateHeight(a);
    c->lc = T2; if( T2 ) T2->parent = c;
    c->rc = T3; if( T3 ) T3->parent = c; BinTree<T>::updateHeight(c);
    b->lc = a; a->parent = b;
    b->rc = c; c->parent = b; BinTree<T>::updateHeight(b);
    return b;
}

注释: 节点a分别连接T₀和T₁作为左右子树，节点c分别连接T₂和T₃作为左右子树，b的左右孩子分别为a和c

3+4重平衡算法(v是进行操作的节点，p是v 的父节点，g是p的父节点)

//3+4重平衡
template <typename T> BinNodePosi(T) BST<T>::rotateAt( BinNodePosi(T) v){
    BinNodePosi(T) p = v->parent; BinNodePosi(T) g = p->parent;
    if( p->data < g->data)/*zig 如果p是g的左子树*/
        if( v->data < p->data){/*zig-zig*/
            p->parent = g->parent;
            std::cout << v->data  << std::endl;
            return connect34( v, p, g, v->lc, v->rc, p->rc, g->rc);
        }else{/*zig-zag*/
            v->parent = g->parent;
            return connect34( p, v, g,  p->lc, v->lc, v->rc, g->rc);           
        }
    else/*zag 如果p是g的右子树*/
        if( v->data >= p->data){/*zag-zag 如果节点v的左子树非空*/
            p->parent = g->parent;
            return connect34(g, p, v, g->lc, p->lc, v->lc, v->rc);
        }else{/*zag-zig*/
            v->parent = g->parent;
            return connect34( g, v, p, g->lc, v->lc, v->rc, p->rc);
        }
}

7.2.1 AVL树ADT接口

avl类通过继承bst类进行实现，并重写了插入和删除操作。

操作	功能	对象
insert(const T& e)	插入指定词条	avl树
remove(const T& e)	删除指定词条	avl树

7.2.1 AVL树模板

#include"bst.h"
#define IsRoot(x) (!((x).parent))
#define IsLChild(x) (!IsRoot(x)&&(&(x)==(x).parent->lc))
#define FromParentTo(x) (IsRoot(x)?_root:(IsLChild(x)?(x).parent->lc:(x).parent->rc))
#define Banlanced(x) (stature((x).lc)==stature((x).rc))   //判断节点是否理想平衡
#define BalFac(x) (stature((x).lc)-stature((x).rc))    //平衡因子
#define AvlBalanced(x) ((-2<BalFac(x))&&(BalFac(x)<2))
#define tallerChild(x) (\
	stature((x)->lc) > stature((x)->rc)? (x)->lc:( \
	stature((x)->lc) < stature((x)->rc)? (x)->rc:( \
	IsLChild(*(x))? (x)->lc:(x)->rc\
	)\
	)\
	)
 
 
template<typename T> class avl :public bst<T>
{
public:
	binNode<T>* insert(const T& e);    //插入指定词条
	bool remove(const T& e);           //删除指定词条
};

7.2.2 insert

template<typename T> binNode<T>* avl<T>::insert(const T& e)
{
	binNode<T>* &x = search(e);
	if (x) return x;    //若已经存在，则直接返回
 
	binNode<T>* xx = x = new binNode<T>(e, _hot); _size++;
	//检查祖先是否失衡
	for (binNode<T>* g = _hot; g; g = g->parent)
	{
		if (!AvlBalanced(*g))
		{
			FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g)));
			break;
		}
		else
		{
			updateHeight(g);
		}
	}
	return xx;
}

7.2.3 remove

template<typename T> bool avl<T>::remove(const T& e)
{
	binNode<T>* &x = search(e);
	if (!x) return false;    //若目标不存在则删除
	removeAt(x, _hot); _size--;
	for (binNode<T>* g = _hot; g; g = g->parent)
	{
		if (!AvlBalanced(*g))
			g = FromParentTo(*g) = rotateAt(tallerChild(tallerChild(g)));
		updateHeight(g);
	}
	return true;
}

7.2.4 AVL.h

#include "BST.h"

#define Balanced(x) ( stature( (x).lc ) == stature( (x).rc ))//理想平衡条件
#define BalFac(x) ( stature( (x).lc ) - stature( (x).rc ))//平衡因子
#define AvlBalanced(x) ( ( -2 < BalFac(x) ) && ( BalFac(x) < 2 ))//AVL平衡条件
//在左右孩子中取最高者
#define tallerChild(x)( \
    stature( (x)->lc) > stature( (x)->rc) ? (x)->lc :( \
    stature( (x)->lc) < stature( (x)->rc) ? (x)->rc :( \
    IsLChild( *(x))? (x)->lc : (x)->rc \
    )\
    )\
    )

template <typename T> class AVL : public BST<T> {
    public:
        BinNodePosi(T) insert( const T& e);//插入
        bool remove( const T& e);//删除
};


//插入
template <typename T> BinNodePosi(T) AVL<T>::insert( const T& e ){
    BinNodePosi(T) & x = BST<T>::search( e ); if( x ) return x;
    BinNodePosi(T) xx = x = new BinNode<T> ( e, BST<T>::_hot); BST<T>::_size ++;
    for( BinNodePosi(T) g = BST<T>::_hot; g; g = g->parent ){
        
        if( !AvlBalanced( *g )) {
            if( IsRoot(*g)){
                this->_root = BST<T>::rotateAt( (tallerChild(tallerChild(g))));
            }
            else if( g == (*g).parent->lc){
                (*g).parent->lc=BST<T>::rotateAt( (tallerChild(tallerChild(g))));
            }
            else{
                (*g).parent->rc=BST<T>::rotateAt( (tallerChild(tallerChild(g))));
            }
            //std::cout << g->data << std::endl;
            break;
        }else
            BST<T>::updateHeight(g);
    }
    return xx;
}
//删除
template <typename T> bool AVL<T>::remove( const T& e){
    BinNodePosi(T) & x = BST<T>::search (e); if( !x ) return false;
    removeAt( x, BST<T>::_hot); BST<T>::_size--;
    for( BinNodePosi(T) g = BST<T>::_hot; g; g = g->parent ){
        if( !AvlBalanced( *g )) 
            if( IsRoot(*g)){
                this->_root = BST<T>::rotateAt( (tallerChild(tallerChild(g))));
            }
            else if(g == (*g).parent->lc){
                (*g).parent->lc=BST<T>::rotateAt( (tallerChild(tallerChild(g))));
            }
            else{
                (*g).parent->rc=BST<T>::rotateAt( (tallerChild(tallerChild(g))));
            }
        BST<T>::updateHeight(g);
        
    }
    return true;
}

7.2.5 测试AVL树

#include "AVL.h"
#include <iostream>
template<typename T> void returnValue(T& a)
{
    std::cout << "return_value: " << a << std::endl;
}
int main(){
    AVL<int> avl;
    avl.insertAsRoot(36);
    avl.insert(27);
    avl.insert(58); 
    avl.insert(21);
    avl.insert(35);
    /*                   36
            27                          58
        21        35                              
    */
    avl.remove(58); //前序遍历结果：35，27，21，36
    /*                    35
             27                         36
        21                      
    */
    avl.insert(15);//前序遍历结果：35，21,15,27,36
    /*                    35
             21                         36
        15         27                      
    */

    void (* visit)(int& ) = &returnValue;//中序遍历
	avl.traverse(avl.root(),visit);
}

ZXG20000

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
7.2 AVL树

参考博客：https://blog.csdn.net/zfliu96/article/details/88538645参考博客：https://blog.csdn.net/weixin_41698717/article/details/107613262本章问题1.AVL树的基础操作有哪些操作功能zig 旋转-顺时针旋转实现等价前提下的局部拓扑调整zag旋转-逆时针旋转实现等价前提下的局部拓扑调整注意：在下列图片之中，圆圈表示的节点，矩形表示的子树zig旋转 -
复制链接

扫一扫