算法设计与分析实验报告（完整代码）

实验一 分治法求众数问题（或…）

一、实验目的

掌握递归与分治方法的基本设计思想与原则，学会递归技术编程技巧。

二、实验内容

1、问题描述

给定含有n个元素的的集合S，求出集合S中的众数。

（或 在有序序列（r1,r2,…,rn）中求ri=i的元素）

2、实验要求

学习分治求解的思想，并使用递归与分治的方法求解。

三、完整代码

1、求众数

#include <iostream> 
#include <vector>   
#include <map>      
using namespace std;

// 定义一个函数，用于查找给定数组的众数   分治法
int findMode(const vector<int>& nums, int left, int right) {
    // 如果左边界等于右边界，说明只有一个元素，直接返回该元素作为众数
    if (left == right) {
        return nums[left];
    }

    // 计算中间位置
    int mid = left + (right - left) / 2;
    // 递归查找左半部分的众数
    int leftMode = findMode(nums, left, mid);
    // 递归查找右半部分的众数
    int rightMode = findMode(nums, mid + 1, right);

    // 创建一个映射count，用于统计每个元素出现的次数
    map<int, int> count;
    //通过遍历数组中的元素，将每个元素作为键，出现次数作为值，存储到映射中。
    for (int i = left; i <= right; ++i) {
        count[nums[i]]++;
    }

    // 获取左半部分众数的出现次数
    int leftCount = count[leftMode];
    // 获取右半部分众数的出现次数
    int rightCount = count[rightMode];

    // 根据出现次数比较左右两部分的众数，返回出现次数较多的那个
    if (leftCount > rightCount) {
        return leftMode;
    }
    else if (leftCount < rightCount) {
        return rightMode;
    }
    else {
        // 如果左右两部分众数出现次数相同，则返回较大的那个
        return max(leftMode, rightMode);
    }
}

int main() {
    // 定义一个包含重复元素的数组
    vector<int> nums = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 1, 1, 2, 2, 3, 3, 3, 3 };
    // 调用findMode函数查找众数，并将结果存储在变量mode中
    int mode = findMode(nums, 0, nums.size() - 1);
    cout << "{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 1, 1, 2, 2, 3, 3, 3, 3 }的众数是： " << mode << endl;
    return 0;
}


/*这段代码实现了一个名为findMode的函数，它接受一个整数类型的向量nums和两个整数类型的参数left和right，表示要查找的数组范围。
  函数的目的是找到给定数组中的众数并返回。
  首先，函数检查左边界是否等于右边界，如果是，则说明只有一个元素，直接返回该元素作为众数。
  否则，函数会计算中间位置mid，然后递归地在左半部分和右半部分分别查找众数。
  这是通过调用findMode函数实现的，传入左边界、中间位置加一和右边界作为参数。
  接下来，函数创建一个映射count，用于统计每个元素出现的次数。
  通过遍历数组中的元素，将每个元素作为键，出现次数作为值，存储到映射中。
  然后，函数获取左半部分众数leftMode和右半部分众数rightMode的出现次数。
  通过查询映射count，可以获取这两个众数的出现次数。
  最后，函数根据出现次数比较左右两部分的众数。如果左半部分众数的出现次数大于右半部分众数的出现次数，则返回左半部分众数；
  如果左半部分众数的出现次数小于右半部分众数的出现次数，则返回右半部分众数；
  如果左右两部分众数出现次数相同，则返回较大的那个。这是通过使用条件语句和比较运算符来实现的。
  在main函数中，定义了一个包含重复元素的数组nums，然后调用findMode函数来查找众数，并将结果存储在变量mode中。
  最后，输出众数的值。*/

（2）有序序列

#include <iostream>
#include <vector>

using namespace std;

// 分治求解函数
int findElement(const vector<int>& arr, int left, int right, int i) {
    if (left > right) {
        return -1; // 未找到元素，返回-1
    }

    int mid = left + (right - left) / 2;

    if (arr[mid] == i) {
        return arr[mid]; // 找到元素，返回该元素
    }
    else if (arr[mid] > i) {
        return findElement(arr, left, mid - 1, i); // 在左半部分继续查找
    }
    else {
        return findElement(arr, mid + 1, right, i); // 在右半部分继续查找
    }
}

int main() {
    vector<int> arr = { 1, 3, 5, 7, 9 };
    int i = 5;

    int result = findElement(arr, 0, arr.size() - 1, i);
    if (result != -1) {
        cout << "元素 " << i << " 在有序序列中的位置为： " << result << endl;
    }
    else {
        cout << "元素 " << i << " 不在有序序列中" << endl;
    }

    return 0;
}

四、运行结果

1、求众数

      函数findMode使用分治法查找给定数组众数。首先判断左边界是否等于右边界，如果是，则说明只有一个元素，直接返回该元素作为众数。接着计算中间位置，然后递归地在左半部分和右半部分分别查找众数。最后，通过遍历数组中的元素，统计每个元素出现的次数，并根据出现次数比较左右两部分的众数，返回出现次数较多的那个。如果左右两部分众数出现次数相同，则返回较大的那个。

2、有序序列

       findElement函数的目的是在有序数组arr中查找元素i。首先，函数检查left是否大于right。如果是，说明在数组中没有找到目标元素，因此返回-1。接下来，计算中间位置mid，即left和right的平均值。这里使用了整数除法，确保结果为整数。然后，函数比较数组中位于中间位置的元素arr[mid]与目标元素i的大小关系。如果它们相等，说明找到了目标元素，直接返回该元素。如果arr[mid]大于i，说明目标元素可能在数组的左半部分。因此，函数递归调用自身，将左边界更新为left，右边界更新为mid - 1，继续在左半部分查找目标元素。如果arr[mid]小于i，说明目标元素可能在数组的右半部分。因此，函数递归调用自身，将左边界更新为mid + 1，右边界更新为right，继续在右半部分查找目标元素。通过不断缩小搜索范围，直到找到目标元素或确定目标元素不存在于数组中为止。

五、实验总结

      通过本次实验，我掌握了递归与分治方法的基本设计思想与原则，练习了递归技术编程技巧。在实验过程中，我学习了分治求解的思想，并使用递归与分治的方法求解了给定含有n个元素的集合S中的众数问题。同时，也尝试了在有序序列中求ri=i的元素的问题。在代码实现过程中，我首先定义了一个函数findMode，用于查找给定数组的众数。在这个函数中，采用了分治法的思想，将数组分为左右两部分，分别递归地查找左半部分和右半部分的众数。然后，创建了一个映射count，用于统计每个元素出现的次数。最后，我们根据出现次数比较左右两部分的众数，返回出现次数较多的那个。如果左右两部分众数出现次数相同，则返回较大的那个。通过运行结果，可以看到函数findMode能够正确地找到给定数组的众数。这说明我的分治法实现是正确的。总的来说，本次实验让我更加深入地理解了递归与分治方法的原理和应用，为我今后解决类似问题提供了有力的支持。

实验二  动态规划法求单源最短路径问题

一、实验目的

熟练掌握动态规划法的设计思想与技巧。

二、实验内容

1、问题描述

求下图中源点到终点的最短路径。

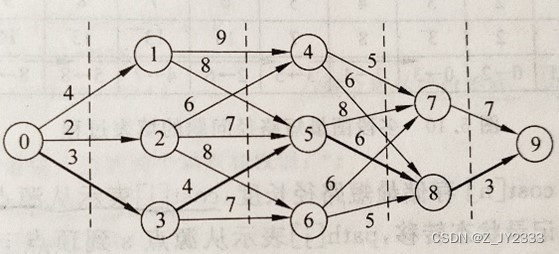
2、实验要求

使用动态规划法来求解此问题。

三、完整代码

#include <iostream> 
#include <vector>   
#include <climits>  
using namespace std; 

// 定义图的边结构，包含目标节点和权重
struct Edge 
{
    int dest, weight;
};

// 定义图的结构，包含节点数 V 和邻接列表 adjList
struct Graph 
{
    int V;
    vector<vector<Edge>> adjList;
};

// 递归和动态规划求解最短路径
int dp(const Graph& graph, int src, int dest, vector<vector<int>>& memo)  //vector<vector<int>>& memo：表示一个二维向量，用于存储已经计算过的子问题的解。这样可以避免重复计算，提高算法的效率。
{
    if (src == dest) 
    { // 如果源节点等于目标节点，说明已经到达目的地，距离为0
        return 0;
    }

    // 如果已经计算过从src到dest的最短路径，直接返回memo中的结果
    if (memo[src][dest] != -1) 
    {
        return memo[src][dest];
    }

    int minDistance = INT_MAX; // 初始化最小距离为整数极限,用于初始化最短距离和判断是否存在路径。

    // 遍历源节点的邻接列表
    for (const Edge& edge : graph.adjList[src]) 
    {
        int nextNode = edge.dest; // 获取下一个节点
        int weight = edge.weight; // 获取边的权重

        // 递归计算从nextNode到dest的最短路径
        int distance = dp(graph, nextNode, dest, memo);

        // 更新最短路径
        if (distance != INT_MAX) 
        {
            minDistance = min(minDistance, weight + distance);
        }
    }

    // 将计算结果保存在memo中
    memo[src][dest] = minDistance;

    return minDistance; // 返回最短路径
}

// 主函数
int main() {
    Graph graph = { // 定义图的结构
        10, // 节点数为10
        { // 邻接列表
            {{1, 4}, {2, 2}, {3, 3}}, 
            {{4, 9}, {5, 8}}, 
            {{4, 6}, {5, 7}, {6, 8}}, 
            {{5, 4}, {6, 7}}, 
            {{7, 5}, {8, 6}}, 
            {{7, 8}, {8, 6}}, 
            {{7, 6}, {8, 5}}, 
            {{9, 7}}, 
            {{9, 3}}, 
            {} 
        }
    };
    int src = 0, dest = 9; // 定义源节点和目标节点

    // 初始化memo数组，创建了一个大小为 graph.V 行、graph.V 列的二维向量，并将所有元素初始化为 -1。
    vector<vector<int>> memo(graph.V, vector<int>(graph.V, -1));

    // 调用dp函数求解最短路径
    int shortestPath = dp(graph, src, dest, memo);

    // 输出最短路径
    if (shortestPath == INT_MAX) 
    {
        cout << "从源节点 " << src << " 到节点 " << dest << " 不存在路径。" << endl;
    }
    else 
    {
        cout << "从源节点 " << src << " 到节点 " << dest << " 的最短距离为 " << shortestPath << endl;
    }

    return 0;
}

/*
首先，定义了两个结构体，Edge和Graph。Edge表示图的边，包含目标节点和权重；Graph表示图的结构，包含节点数V和邻接列表adjList。
然后，实现了一个名为dp的递归函数，用于求解从源节点到目标节点的最短路径。
该函数接受四个参数：图graph、源节点src、目标节点dest和一个二维向量memo。memo用于存储已经计算过的子问题的解，避免重复计算。
在dp函数中，首先判断源节点是否等于目标节点，如果是，则说明已经到达目的地，距离为0，直接返回0。
如果已经计算过从源节点到目标节点的最短路径，则直接从memo中返回结果。
接下来，初始化最小距离minDistance为整数极限INT_MAX，用于初始化最短距离和判断是否存在路径。
遍历源节点的邻接列表，对于每个邻接节点，获取下一个节点nextNode和边的权重weight。
递归调用dp函数，计算从nextNode到目标节点的最短路径distance。
如果distance不等于INT_MAX，说明存在从nextNode到目标节点的路径，更新最小距离minDistance为当前最小距离和weight+distance中的较小值。
将计算结果保存在memo中，以便后续使用。
最后，返回最小距离minDistance作为从源节点到目标节点的最短路径。
在主函数中，定义了一个图graph，包含了节点数V和邻接列表adjList。然后定义了源节点src和目标节点dest。
初始化memo数组，创建了一个大小为graph.V行、graph.V列的二维向量，并将所有元素初始化为-1。
调用dp函数求解最短路径，并将结果保存在shortestPath变量中。
根据shortestPath的值判断是否存在路径，如果等于INT_MAX，则输出不存在路径的信息；否则，输出最短路径的结果。
*/

四、运行结果

      递归和动态规划求解最短路径的函数dp，它接收一个图、源节点、目标节点和一个用于存储已经计算过的子问题的解的二维向量作为参数。如果从源节点到目标节点的最短路径已经被计算过，那么直接返回这个结果；否则，遍历源节点的所有邻接节点，递归地计算从这些邻接节点到目标节点的最短路径，并更新最短路径。最后，将计算结果保存在二维向量中，并返回最短路径。

五、实验总结

      在本次实验中，我使用动态规划法来求解单源最短路径问题。通过编写代码，我实现了一个名为dp的函数，该函数接收一个图、源节点、目标节点和一个用于存储已经计算过的子问题的解的二维向量作为参数。如果从源节点到目标节点的最短路径已经被计算过，那么直接返回这个结果；否则，遍历源节点的所有邻接节点，递归地计算从这些邻接节点到目标节点的最短路径，并更新最短路径。最后，将计算结果保存在二维向量中，并返回最短路径。

      通过本次实验，我掌握了动态规划法的设计思想与技巧。首先，需要明确问题的描述和要求，然后设计合适的状态转移方程，最后通过递归和动态规划的方法求解问题。在这个过程中，还需要注意避免重复计算，提高算法的效率。

实验三  贪心法求汽车加油问题

一、实验目的

熟练掌握贪心法的设计思想与技巧。

二、实验内容

1、问题描述

一辆汽车加满油后可行驶n公里，旅途中有k个加油站。求解如下问题：汽车应在哪些加油站停靠加油，使沿途加油次数最少。

2、实验要求

使用贪心法来求解该问题。

三、完整代码

#include <iostream>
using namespace std;

int n = 30;//加满油后可行驶的距离
const int m = 10;  //加油站个数
int A[m] = { 10,15,10,17,8,17,13,9,11,10 };//加油站距离（为i-1与i之间的距离）
int main() {
    int s = n;//当前剩余油量可行驶距离
    int flag[m] = { 0,0,0,0,0,0,0,0,0,0 };//记录加油站索引
    int k = 0;//加油站个数记录
    for (int i = 0; i < m; i++)
    {
        if (n < A[i])
        {
            cout << "no solution!" << endl;
            break;
        }
        if (s - A[i] >= 0)
        {
            s -= A[i];
        }
        else
        {
            s = n - A[i];
            flag[k++] = i - 1;
        }
    }
    int a = 0;
    cout << "the need stations are:" << endl;
    while (flag[a] != 0)
        cout << flag[a++] << ",";
    return 0;
}

四、运行结果

      首先，定义了一个变量n表示加满油后可行驶的距离，一个常量m表示加油站的个数，以及一个数组A表示每个加油站之间的距离。然后，通过一个for循环遍历每个加油站，如果当前距离小于下一个加油站的距离，说明无法到达下一个加油站，输出"no solution!"并结束循环。如果当前距离大于等于下一个加油站的距离，将当前距离减去下一个加油站的距离。如果当前距离小于0，说明需要加油，将当前加油站的索引存入flag数组，并将当前距离设置为n减去当前加油站的距离。最后，输出需要加油的加油站的索引。

五、实验总结

      通过本次实验熟练掌握了贪心法的设计思想与技巧，贪心法是选取局部最优达到全局最优的一种算法，相对而言运用较为广泛，在本次实验中通过解决汽车加油问题对贪心法进一步进行了理解以及学习。代码实现过程虽然比较简单，也借鉴了上课老师讲的思路以及参考书上的过程进行了实现，细节部分进行了优化，在输入部分未采用动态输入，直接使用预置参数较为简单。

实验四  回溯法求0/1背包问题

一、实验目的

掌握回溯法的基本设计思想与原则。

二、实验内容

1、问题描述

给定n个重量为{w1,w2,…,wn}的物品，其价值为{v1,v2,…,vn} ，另有一个容量为C的背包，求这个物品中一个最有价值的子集使得在满足背包的容量的前提下，包内的总价值最大。

2、实验要求

使用回溯法来求解该问题。

三、完整代码

#include<iostream>
#include<stack>//使用栈（后进先出）
using namespace std;

int maxValue(int w[], int v[], const unsigned& length, const unsigned& capacity)
{
    stack<int> Bag;//首先构造出一个空的背包
    int max = 0;//不同装入情况中背包中物品最大的价值
    int weight = 0;//当前背包中物品的总重量
    int value = 0;//当前背包中物品的总价值
    int i;

    for (i = 0; ; i++)
    {
        if (weight + w[i] <= capacity)//背包装入该物品后不会超重
        {
            Bag.push(i);//入栈
            weight += w[i];
            value += v[i];
        }
        if (i == length - 1)
        {
            //接下来将本次装包物品价值与当前最高的装包物品价值进行比较，保留较大的一个
            if (max < value)
            {
                max = value;
            }
            //此时取出最后装进包里的一件物品并对其下一件物品进行考虑——回溯法核心
            {
                i = Bag.top();//取出上一件装入的东西（回溯的过程）
                Bag.pop();
                weight -= w[i];
                value -= v[i];
                if (i == length - 1)//特殊情况：如果最后装进包里的物品本来在就是编号最大的物品，那么它后面就没有其他物品了，循环必定终止
                {
                    if (Bag.empty())break;//当所有物品都被从包中拿出来后，这是说明已经遍历完所有情况，查找结束（相当于解空间树中最右边的子树已经走完了）
                    i = Bag.top();//取出上一件装入的东西，这就是回溯的过程
                    Bag.pop();
                    weight -= w[i];
                    value -= v[i];
                }
            }
        }
    }
    return max;
}

int main()
{
    unsigned num, capacity;
    cout << "please enter the number of items:";
    cin >> num;
    int* weights = new int[num];
    int* values = new int[num];
    cout << "please enter the weight of each item:";
    for (unsigned i = 0; i < num; i++)
    {
        cin >> weights[i];
    }
    cout << "please enter the value of each item:";
    for (unsigned i = 0; i < num; i++)
    {
        cin >> values[i];
    }
    cout << "please enter the capacity of the bag:";
    cin >> capacity;
    cout << "the optimal solution to this problem of Backtracking is:" << maxValue(weights, values, num, capacity);
    return 0;
}

四、运行结果

      maxValue函数实现了一个0-1背包问题的动态规划解法。这个函数接收四个参数：物品的重量数组w、物品的价值数组v、物品的数量length和背包的容量capacity。函数返回的是能够装入背包的物品的最大总价值。

五、实验总结

通过本次实验，熟练掌握回溯法的基本设计思想与原则，回溯法是借鉴树的深度优先遍历实现的算法，相较于普通的遍历，大大的节省了时间。我在项目中进行了实践以及检验，代码部分：根据先入后出的特性采用栈作为背包，选取数组作为相应的参数输入，回溯法部分采用栈的出栈入栈，取出栈顶元素进行实现，在细节部分也进行了相关优化，经过本次实验，对于回溯法的和核心思想以及原理已经熟练掌握。