浅谈队列及栈的用法

浅谈队列及栈的用法

STL中的queue以及stack是两个十分好用的数据结构，也是最简单的数据结构。在这里简单的介绍一下它们的用法。

---

队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。 —— [ 百度百科 ]

正常来讲，如果不用STL的话，我们则需要自己动手手写队列，但大家可以先看一下下面的代码：
Code：

#include<stdio.h>
struct queue
{
    int data[100];
    int head;
    int tail;
};
int main()
{
    struct queue q;
    //初始化队列 
    q.head=1;
    q.tail=1;
    for(int i=1;i<=9;i++)
    {
        scanf("%d",&q.data[q.tail]);
        q.tail++; 
    }
    while(q.head<q.tail)//当队列不为空的时候执行循环 
    {
        //打印队首并将队首出队 
        printf("%d ",q.data[q.head]);
        q.head++;
        //先将新队首的数添加到队尾 
        q.data[q.tail]=q.data[q.head];
        q.tail++;
        //再将队首出队 
        q.head++;
    }
    return 0;
}

手写队列使用一个que[]数组来模拟一个队列，head,tail，分别代表着队列的头和尾，这样的方法不仅麻烦而且看起来也不美观，而STL就不一样了。
形象的讲，队列是这个样子：

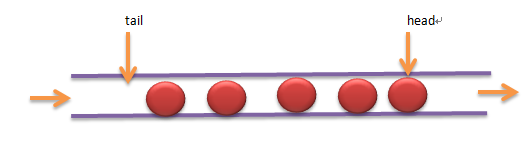
因此，队列的重要性质就是：
先进先出（FIFO)——先进队列的元素先出队列。来源于我们生活中的队列（先排队的先办完事）。

一些常用函数：

• back() 返回最后一个元素
• empty() 如果队列空则返回真
• front() 返回第一个元素
• pop() 删除第一个元素
• push() 在末尾加入一个元素
• size() 返回队列中元素的个数

Add：queue的工作效率一般不高，如想优化可以采用循环的方式，即像一个动态的圈圈的“循环队列”.

优先队列 （Priority queue）

之所以叫优先队列是因为在这个队列中，我们可以让其自动排好顺序，然后再O(1)时间内得到我们想要的答案。它的好处就不多说了，谁都有过体会。

下面介绍一下写的两种姿势：

[NOIP2004]的合并果子就是一道十分经典的优先队列的题目。

#include<stdio.h>
#include <cstdio>
#include<algorithm>
#include<queue>
using namespace std;
struct node
{
    int x;
};
bool operator< (node a,node b)
{
    return a.x > b.x;
}
priority_queue<node,vector<node> >Q;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        node t;
        scanf("%d",&t.x);
        Q.push(t);
    }
    int head,end;
    int sum=0;
    for(int i=1;i<n;i++)
    {
        node head=Q.top();
        Q.pop();
        node end=Q.top();
        Q.pop();
        sum+=head.x+end.x;
        head.x=head.x+end.x;
        Q.push(head);
    }
    printf("%d",sum);
}

我们可以称这种书写方式为“结构体”版，因为我们可以不断构建新的结构体来进行操作，但个人感觉会很乱，因为谁没事会往结构体里放数啊，用个数组不行吗？。。
因此，隆重介绍第二种方式，我姑且先称之为“数组”版：
POJ2823 是一道优先队列的模板题：

#include<stdio.h>
#include<string.h>
#define MAXN 1000000+100 
#include<queue>
using namespace std;
int a[MAXN],min_num[MAXN],max_num[MAXN],cnt1,cnt2;
struct cmp1
{
    bool operator()(const int a1,const int a2)
    {
        return a[a1]>a[a2];
    }
};
struct cmp2
{
    bool operator()(const int a1,const int a2)
    {
        return a[a1]<a[a2];
    }
};
priority_queue<int,vector<int>,cmp1>q1;
priority_queue<int,vector<int>,cmp2>q2;
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",a+i);
    }
    for(int i=1;i<=k;i++)
    {
        q1.push(i);
        q2.push(i);
    }
    min_num[++cnt1]=a[q1.top()];
    max_num[++cnt2]=a[q2.top()];
    for(int i=k+1;i<=n;i++)
    {
        q1.push(i),q2.push(i);
        while(i-q1.top()>=k)
        {
            q1.pop();
        }
        min_num[++cnt1]=a[q1.top()];
        while(i-q2.top()>=k)
        {
            q2.pop();
        }
        max_num[++cnt2]=a[q2.top()];
    }
    for(int i=1;i<=cnt1;i++)
    {
        printf("%d ",min_num[i]);
    }
    printf("\n");
    for(int i=1;i<=cnt2;i++)
    {
        printf("%d ",max_num[i]);
    }
    return 0;
}

在这里可以看到，我们还是正常的用数组，只不过用一个结构体重载一下cmp，不仅看起来美观，而且用起来十分方便。但不管怎么说，习惯什么用什么才是做题的第一准则。

---

栈

栈（stack）又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。 —— [ 百度百科 ]

栈这种东西就好理解多了，先上图：

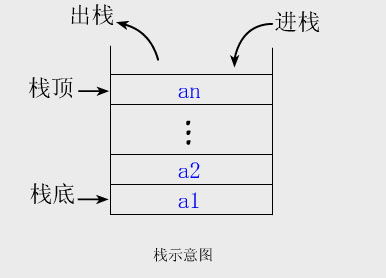
与队列不同的是，栈内的元素不是先进先出，相反，是一种类似于“后来居上”的感觉，先进去的处在栈底，而后来的则在上面。

一些常用函数：

• empty() 堆栈为空则返回真
• pop() 移除栈顶元素
• push() 在栈顶增加元素
• size() 返回栈中元素数目
• top() 返回栈顶元素

先举个小例子，我们可以用栈来判断一个数字是否回文:
Code:

#include<stdio.h>
#include<string.h>
char a[101],s[101]; 
int main()
{
    gets(a);
    int len=strlen(a);
    int mid,next;//找到中点 以及 需要进行字符匹配的起始下标 
    if(len%2==0)
    {
        mid=len/2-1;
        next=mid+1;
    }
    else
    {
        mid=len/2-1;
        next=mid+2;
    }
    int top=0;//栈的初始化 
    for(int i=0;i<=mid;i++)//将mid前的字符依次入栈 
    {
        s[++top]=a[i];
    }
    for(int i=next;i<=len-1;i++)//开始匹配 
    {
        if(a[i]!=s[top])
        {
            break;
        }
        top--;
    }
    if(top==0)
    {
        printf("YES.\n"); 
    }
    else
    {
        printf("NO.\n");
    }
    return 0;
}

看起来没什么不同是吧，而且好像更麻烦了。也许我的例子举得并不恰当，但栈的应用还是比较广泛的。在继续往下谈论之前，一个特别重要的知识一定要想清楚，那就是：
出栈顺序!!
最开始很容易出现这样的一个思想误区，那就是比如：12345进栈，则只有54321这一种出栈顺序，但是事实并非如此。
Because,有可能1刚进栈就出栈了，其它数全进去了才出，就会产生15432，以此类推就可以；相反43512就不行，因为当4首先出栈，则说明1，2，3三个元素已经入栈，则出栈序列中1不可能在2之前。
为了解决这个问题，POJ有一道十分好的题，POJ1363赤裸裸的判断出栈顺序是否合法。如果正常的模拟时间复杂度为O(n^2)，但O(n)的算法就是简单的模拟入栈出栈，So easy.
Code：

#include<stdio.h>
#include<string.h>
#include<stack>
using namespace std;
int n;
int a[1500];
bool simulate()
{
    stack<int>s;
    int tmp=1;
    for(int i=1;i<=n;i++)
    {
        while(tmp<=a[i])
        {
            s.push(tmp++);
        }
        int x=s.top();
        s.pop();
        if(x!=a[i])
            return false;
    }
    return true;
}
int main()
{
    while(~scanf("%d",&n)&&n)
    {
        while(~scanf("%d",&a[1])&&a[1])
        {
            for(int i=2;i<=n;i++)
            {
                scanf("%d",&a[i]);
            }   
            if(simulate())
            {
                puts("Yes");
            }
            else
            {
                puts("No");
            }
        }
        printf("\n");
    }
    return 0;
}

单调栈

就像队列有优先队列一样，为什么我们的栈不能有类似的性质？？
这个可以有。
单调栈与单调队列很相似。首先栈是后进先出的，单调性指的是严格的递增或者递减。
PS：
单调栈有以下两个性质：
1、若是单调递增栈，则从栈顶到栈底的元素是严格递增的。若是单调递减栈，则从栈顶到栈底的元素是严格递减的。
2、越靠近栈顶的元素越后进栈。
单调栈与单调队列不同的地方在于栈只能在栈顶操作，因此一般在应用单调栈的地方不限定它的大小，否则会造成元素无法进栈。
元素进栈过程：对于单调递增栈，若当前进栈元素为e，从栈顶开始遍历元素，把小于e或者等于e的元素弹出栈，直接遇到一个大于e的元素或者栈为空为止，然后再把e压入栈中。对于单调递减栈，则每次弹出的是大于e或者等于e的元素。
举一个单调递增栈的例子：

进栈元素分别为3，4，2，6，4，5，2，3

3进栈：（3）
3出栈，4进栈：（4）
2进栈：（4，2）
2出栈，4出栈，6进栈：（6）
4进栈：（6，4）
4出栈，5进栈：（6，5）
2进栈：（6，5，2）
2出栈，3进栈：（6，5，3）

还是上一道题吧：
POJ2559Largest Rectangle in a Histogram
题意就是在单位长度内，每一个矩形的宽都为1，但长度可变，题意需要求最大矩形的面积。
因此我们可以用两个数组l[i],r[i]表示，第i个点向左/右 最长能扩展到第几个点，也就是第一个小于它的点。
Ans=max{a[i]*(r[i]-l[i]+1)};
在这里我们就要用的“单调栈”来进行这神奇的功能，让时间复杂度由O(n^2)变为O(n).

#include<stdio.h>
#include<string.h>
#include<stack>
#define MAXN 100005
typedef long long ll;
using namespace std;
ll n,x=0;
ll a[MAXN],l[MAXN],r[MAXN];
stack<int>s;
ll max(ll a,ll b){return a>b?a:b;}
int main()
{
    while(~scanf("%lld",&n)&&n)
    {
        for(ll i=1;i<=n;i++)
        {
            scanf("%lld",a+i);
        }
        while(!s.empty())s.pop();
        s.push(0); 
        a[0]=a[n+1]=-1;
        for(ll i=1;i<=n;i++)
        {
            for(x=s.top();a[x]>=a[i];x=s.top())
            {
                s.pop();
            }
            l[i]=x+1;
            s.push(i);
        }
        while(!s.empty())s.pop();
        s.push(n+1); 
        for(ll i=n;i>=1;i--)
        {
            for(x=s.top();a[x]>=a[i];x=s.top())
            {
                s.pop();
            }
            r[i]=x-1;
            s.push(i);
        }
        ll max_num=-1;
        for(ll i=1;i<=n;i++)
        {
            max_num=max(max_num,(r[i]-l[i]+1)*a[i]);
        }
        printf("%lld\n",max_num);
    }
    return 0;
}