关于并查集(union find) 算法基本原理以及其在分布式图场景的应用

z_stand

已于 2022-02-27 15:17:34 修改

阅读量2.2k

点赞数

分类专栏：分布式框架数据结构和算法 # 数据结构：线性表文章标签：算法分布式数据结构

于 2022-02-27 13:54:10 首次发布

本文链接：https://blog.csdn.net/Z_Stand/article/details/123157296

版权

数据结构和算法同时被 3 个专栏收录

42 篇文章

订阅专栏

数据结构：线性表

18 篇文章

订阅专栏

分布式框架

9 篇文章

订阅专栏

二月的最后一篇水文…想写一些有意思的东西。

文章目录

环检测在图数据结构中的应用

我们在图数据结构场景中会有一些判断是否存在环的需求，大多数的判断场景是在有向图中：

比如我们在图数据存储场景中想要拓扑好友关系，比如查找某一个人到另一个人的好友关系链，这个检索过程需要是一个有向无环图的检索过程，是不能出现环的，需要在检索过程中能够检测到环的存在。
再比如我们在分布式事务场景中，比如悲观事务的实现中往往需要有一个单key 事务锁在并发场景的 wait 锁关系的构造 Rocksb 事务锁实现 – 死锁检测部分，这个时候需要对多个事务的 wait锁之间的互相等待关系构造一个 wait-circle，并且需要在一个元素插入之后检测改有向图是否存在环，存在则需要回退这次的插入。

当然，实际应用到图存储/计算的场景还有很多，对环的检测需求也都是一直存在的。

深度/广度优先检测环

在这种场景下我们一般检测环存在的做法是遍历图，主要使用两种方式 (bfs/dfs) :
这两种实现方式都比较简单，利用一个visited 数组保证访问过程中除非遇到环，否则不会访问到自己。
下面这个有向图在遍历的过程中会出现环，在分布式事务的场景下 wait-circle 就是出现死锁了，这种情况下是必须要检测出环的。
在这里插入图片描述

如下使用深度优先搜索来进行环的查找，前置条件就是使用邻接矩阵来标识图中的顶点，比如坐标[i,j] = 1，标识i --> j 即顶点 i 和顶点 j 连通；为 0 则表示两个顶点不连通。
查找的算法也很简单：

增加辅助访问数组 visited，标识顶点 i 被访问过。
遍历邻接矩阵且 visited 为 false 的顶点
深度优先搜索所有以 i 为顶点的 [i,j] = 1 即 i --> j ，i --> k的顶点，如果发现某一个顶点 visited[j]=true，那么就标识已经找到环了，否则继续深度优先查找。

// 通过邻接矩阵 matrix 保存有向图 
vector<vector<int>> matrix;
bool isCircle(）{
	// 初始化visit 数组，标识已经访问过的节点
	int m_size = matrix.size();
	vector<bool> visited(m_size, false);
	for (int i = 0;i < m_size; i++) {
		if (!visited[i]) {
			// 传入当前访问的下标，访问标识数组，最后就是父节点(上一个访问的节点)
			// 找到了环，就返回真即可.
			if (dfs_search(i, visited)) {
				return true;
			}
		}
	}
	// 整个矩阵都遍历完成还是没有找到，就认为是无环
	return false;
}

// dfs 查找环
bool dfs_search(int current_idx, vector<bool>& visited) {
	visited[current_index] = true;
	// 查找 current_idx 即当前节点的连通节点
	for (int i = 0;i < matrix[current_idx].size(); i++) {
		// 如果为1，则标识当前current_idx 指向 i，那么check一下这个指向的节点是否访问过，
		// 那就是找到环了。
		if (matrix[current_idx][i] == 1) {
			if ( visited[i] && i != current_idx) return true;
			else {
				if (dfs_search(i, visited)) return true;
			}
		}
	}
	return false;
}

广度优先算法也很类似（层次遍历），同样是通过visited 辅助数组来实。
和dfs的差异只是利用队列来提前将 current_idx 的所有指向的兄弟节点先添加到队列中，再进行下一层的查找，如下代码。

// 通过邻接矩阵 matrix 保存有向图 
vector<vector<int>> matrix;
bool isCircle(）{
	int m_size = matrix.size();
	vector<bool> visited(m_size, false);
	
	// 保存当前访问的顶点
	for (int i = 0;i < m_size; i ++) {
		if (!visited[i]) {
			if (bfs_search(i, visited)) return true;
		}
	}
	return false;
}

bool bfs_search(int curr_idx, vector<bool>& visited) {
	queue<int> qu;
	qu.push(curr_idx);
	visited[curr_idx] = true;
	while (!qu.empty()) {
		int size = qu.size();
		// 按层遍历
		for (int j = 0;j < size; j++) {
			int curr_idx = qu.front();
			qu.pop();
			// 需要将 curr_idx 所有的临接顶点 先check 环是否存在，不存在则添加到queue中
			for (int k = 0;k < matrix[curr_idx].size(); k++) {
				if (matrix[curr_idx][k] == 1) {
					if (curr_idx != k && visited[k]) return true;
					else {
						qu.push(k);
						// 标记 curr_idx --> k 的 k顶点已经被访问过了
						visited[k] = true;
					}
				}
			}
		}
	}
	return false;
}

以上两种实现方式都是非常基础的图中的环的检测，都是是能够正确得检测出环的存在。
但是性能问题却很明显，每一次的检测都需要对整个图进行一个大的scan，对于一个 m*n 的超大矩阵 (我们普通的分布式图存储集群中往往拥有超过百万/千万级别的顶点和总数目近万亿的边)，在这样的图网络中去检测环，利用上面的方式效率可以说是极低的。当然，现在最通用的解决办法就是限制查找的层数。

索引好友关系列表的话也仅仅只会索引3度的出边列表，在分布式事务中的wait-circle 中也会限制死锁检测的深度；但是当我们想要查找两个无关顶点之间的最短到达路径的时候，这个过程中的环检测避免不了，那有没有更加高效的算法，在不用每次插入一个元素都进行一次全链路遍历检测环呢？

当然有～～～, 聪明的人无处不在，并查集 应运而生。

并查集数据结构 (Union-Find)

基本概念

并查集是一种数据结构，其支持对不相交的集合（disjoint sets）执行如下一些操作：

makeSet(e) 这是并查集数据结构中的一个操作，用来将输入的元素 e 插入到一个集合中，并返回包含这个元素e 的集合的根节点。
Union(A,B) 合并两个集合 A,B
Find(e) 返回包含元素e 的集合

基本概念其实是很晦涩的，直接来看并查集的这几个操作就好。
并查集中的集合元素组织有两种形态：链表形态和树形态。
在这里插入图片描述
原本我们的链表/树形态，会记录 parent–>child 或者 prev --> next 这样的关系，而并查集中对数据集的标识是记录 next 的 prev节点或者说是记录 child 的 parent 节点信息。

其中树形态的并查集表示方式其实是链表形态的一种优化（路径压缩），能够极大得降低元素查找的层数；当然，在图的环优化中，这两种形态可以分别用于有向图（链表形态，保存了集合中的方向关系）和无向图（不需要方向关系）的表示。

接下来，我们看看并查集的每个操作实现。

初始化

对集合中的每一个元素，他们的父节点应该为空或者也可以指向自己（指向自己的这种初始化方式就不能应用在图的环判断中了，可以用于正常的集合操作）。

本文演示均用-1 表示空

虽然前面说并查集的数据结构有两种形态， 链表或者树，但是实际我们应用的时候，可以采用数组/无序map 的方式就够了。

unorder_map<int,int> father;
void Add(int ele) {
	if (!father.count(ele)) {
		father[ele] = -1; 
	}
}

合并 union

这个操作主要是check 两个节点是否可以连通（祖先是不同的），如果是连通的，那就要进行合并，让他们拥有相同的祖先。
这里两个节点谁当祖先都是可以的。
在这里插入图片描述

void union(int x, int y) {
	int x_root = find(x);
	int y_root = find(y);
	
	// 祖先不同，则发现是两个不同的集合，则可以对他们进行合并
	if (x_root != y_root) {
		fater[x_root] = y_root;
	}
}

查找祖先

如果节点的父节点不为空，那就需要持续查找，直到找到父节点为空的节点，就是当前输入的ele 的祖先节点。
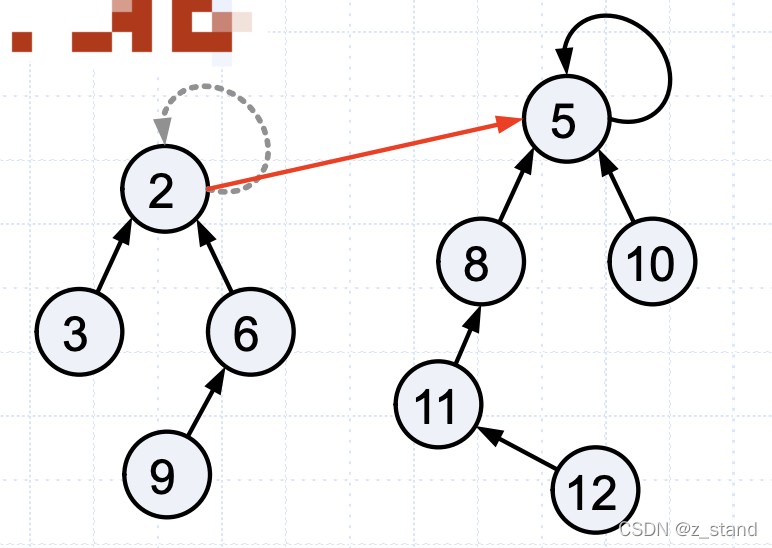
在这里插入图片描述
我们想要查找节点 12 的祖先节点，就需要不断的check father节点，直到father节点为空(或者是自己)。

int find(int ele) {
	int root = ele;
	while (father[root] != -1) {
		root = father[root];
	}
	return root;
}

这里是有可以优化的地方，我们希望在并查集中的节点分布能够更接近树形态，而不是链表形态。毕竟树形查找的复杂度是小于等于(O(log_n))，也就是我们可以将链表形态的并查集结构转换为树形态。
这样做可行的原因是对于并查集中的节点来说连通性是可以传递的，节点之间互相连通的标记只需要拥有一个相同的祖先就好了。

大体过程如下：
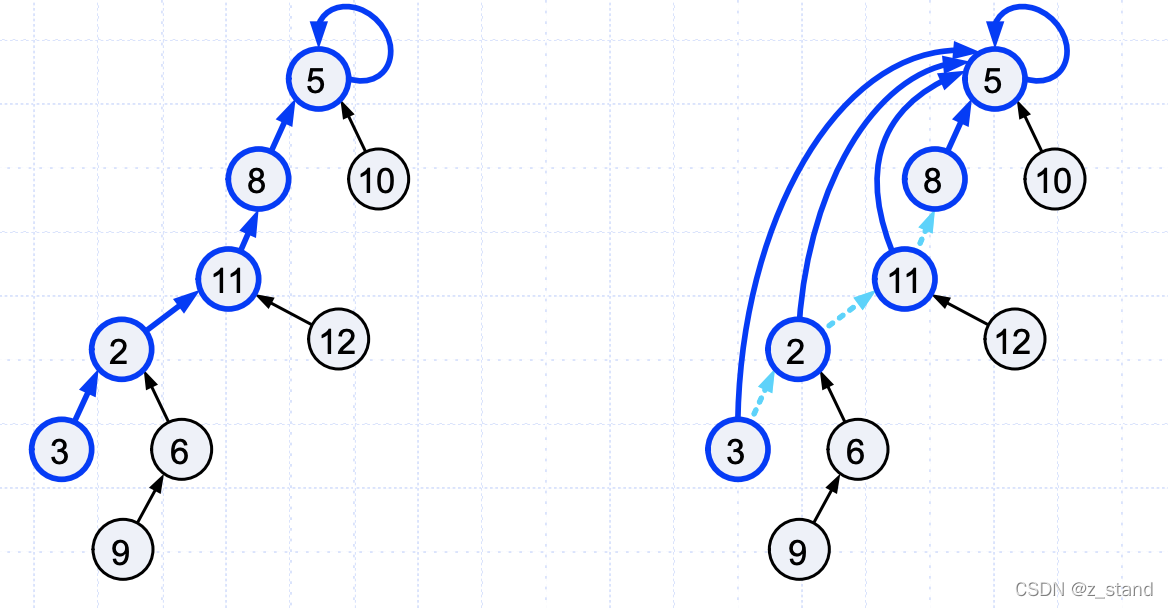
在这里插入图片描述
就是将上图中左侧一段链式结构可以合并成右侧的树形结构。

优化1: 合并过程利用 rank 优化路径

rank 是一个在前面father基础上额外增加的一个数据结构，标识当前节点距离祖先节点的长度，这样我们的初始化以及合并代码就变成下面的样子：

typedef struct UnionFindNode {
	UnionFindNode* father;
	int rank;
	UnionFindNode() : father(nullptr),rank(0) {}

	bool operator==(const UnionFindNode& lhs) {
		return father == lhs.father && rank == lhs.rank;
	}
}Node;

void MakeSet(Node& ele) {
	ele.father = nullptr;
	ele.rank = 0;
}

void Union(const Node x, Node y) {
	// 找到他们的公共祖先节点
	auto xRoot = Find(x);
	auto yRoot = Find(y);
	if (xRoot == yRoot) {
		return;
	}
	
	// 他们不在同一个集合，则需要合并他们的祖先。
	// 将距离比较短的合并到距离长的祖先上。
	if (xRoot->rank < yRoot->rank) {
		xRoot->father = yRoot;
	} else if (xRoot->rank > yRoot->rank) {
		yRoot->father = xRoot;
	} else { //rank 相等，互相指向谁都无所谓，需要增加指向后的被指向节点的rank（增加了一个元素的深度）。
		xRoot->father = yRoot;
		yRoot->rank += 1;
	}
}

优化2: 路径压缩(Path Compression)

当然，以上优化方式也能够利用rank 达到我们将链表转换成树的目的，但是需要一个额外的rank 字段，每一个节点都会多消耗4bytes 的内存。
其实还有一种更简洁优雅的优化方式，就是 路径压缩。

rank 的优化是在 Union 操作的时候，这里路径压缩则是在 Find的时候。

// 还是继续使用基本的 unorder_map 保留信息
unordered_map<int, int> father;

// 查找节点 i 的祖先节点
int Find(int i) {
	int root = i;
	// -1 是我们在最前面 Add 一个新的并查集节点的时候
	// 会将这个节点的父节点设置为 -1，标识它目前是一个单独的集合。
	while(father[root] != -1) {
		root = father[root];
	}

	// 路径压缩的过程
	while (i != root) {
		int origin_father = father[i];
		father[i] = root;// 关键！进行路径压缩，将节点i 的父节点直接指向祖先节点。
		i = origin_father;
	}
	return root;
}

比如对于这样的一个并查集集合，我们想要查找 6。
在这里插入图片描述
经过路径压缩之后， 6 包括整个之前的节点都会尝试进行一次路径压缩。

关于路径压缩的时间复杂度证明较为复杂，这个推演是通过阿克曼函数进行推演的。
总之表示方式是 O(log*n)，其中 log*n表示 n 取多少次 $log_2n$ 并向下取整之后变成1，可以理解为是 O(1) 级别。
比如 log*2^65526 ，2^65536 在阿克曼函数中表示的是 A(4,3) 的结果，基本是人类思维极限的数字，而在 log*n 下仅仅只有 5。

关于路径压缩时间复杂度的推演以及证明可以参考 The math in Union-Find.

并查集解决图中检测环问题

回到我们最初图中检测环的问题，我们接下来可以利用并查集的几个操作轻松解决。

对于 0 --> 1 --> 2，构造出来的并查集结构经过路径压缩是 0 --> 2 <-- 1 ；而如果存在环，也就意味着 2 --> 0，对于并查集来说我们只需要提前 find (0) 和 find(2) 是否相等，如果相等，则认为当前的插入是会造成环的（0 已经存在且其祖先节点是2）。

实现如下：

class UnionFind {
public:
	// void Add
	// void Union
	// int Find
	// bool IsConnected
private:
	unordered_map<int,int> father_;
}
// 通过邻接矩阵 matrix 保存有向图 
vector<vector<int>> matrix;
bool IsCircle() {
	UnionFind uf;
	for (int i = 0;i < matirx.size(); i++) {
		// 添加每一个节点到并查集之中
		uf.Add(i);
		for (int j = 0;j < i; j++) {
			if (matrix[i][j]) {
				int x_root = Find(i);
				int y_root = Find(j);
				// 发现了两个不同节点的祖先节点相等，则找到了环
				if (x_root == y_root && i != j) return true;
					
				// 否则，是两个可以连通的节点，那就需要合并这两个集合（他们的祖先直接合并就好了）。
				if (x_root != y_root) uf.Union(x_root,y_root);
			}
		}
	}
	return false;
}