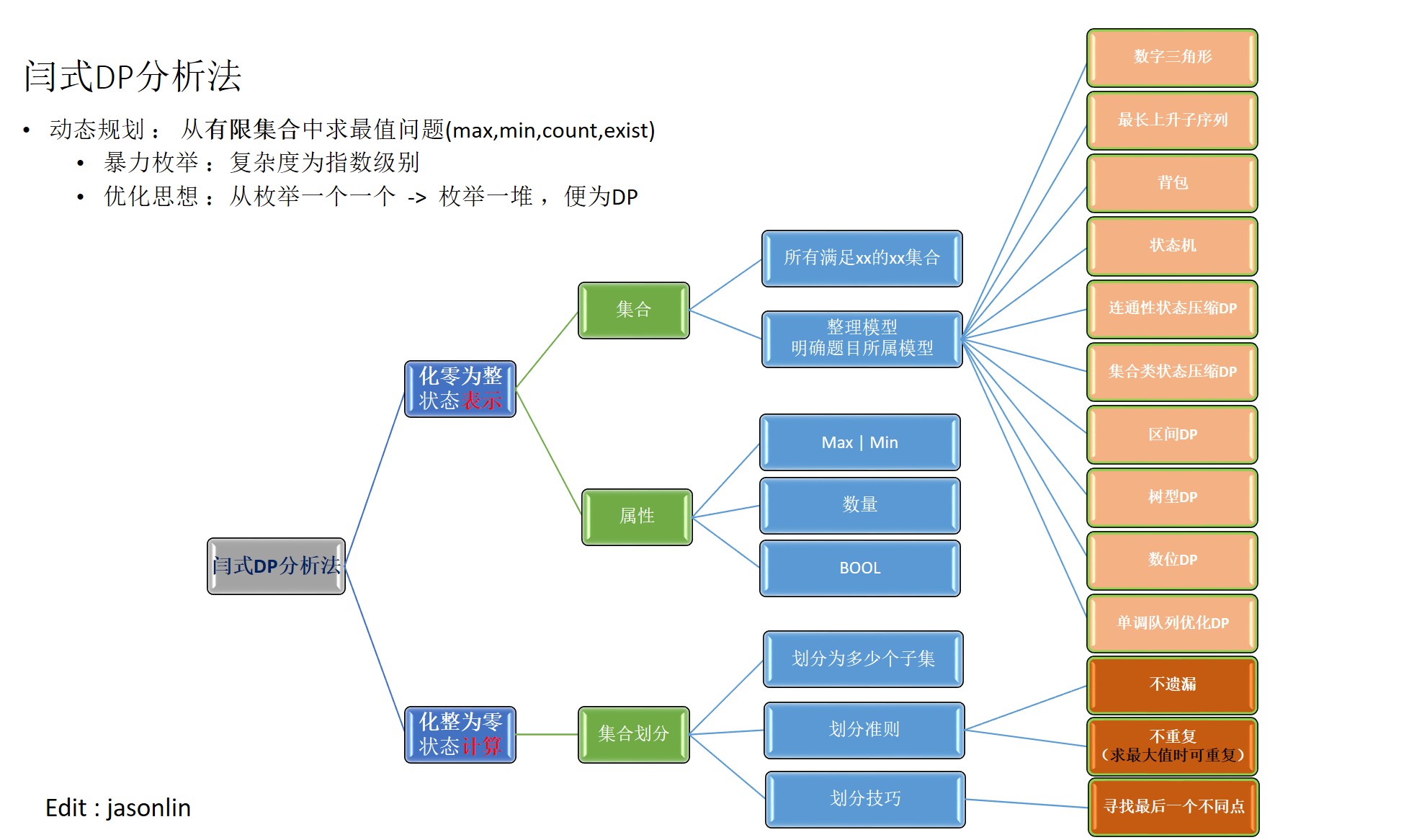
Acwing动态规划算法

动态规划

背包问题

01背包

• 朴素算法

• #include <iostream>
  #include <cstring>
  #include <algorithm>
  #include <cmath>
  using namespace std;
  const int M = 1010;
  int v[M], w[M];
  int f[M][M]; // f[i][j] 前i个数中选择若干个物品，并且其体积之和小于等于j的最大价值
  int main()
  {
      int n , m;
      cin >> n >> m;
      for (int i = 1; i <= n; i ++ ) // 下标从1开始
      {
          cin >> v[i] >> w[i];
      }
      
      for (int i = 1; i <= n; i ++ )
      {
          for(int j = 0; j <= m; j ++)
          {
              f[i][j] = f[i - 1][j]; // 不选择第i个物品
              if(j >= v[i]) // 当j >= v[i] 时，才能选择第i个物品
              {
                  f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); // 不选择第i个物品和，选择第i个物品做对比
              }
          }
      }
      cout << f[n][m] << endl;
      return 0;
  }
  

• 优化后代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;
const int M = 1010;
int v[M], w[M];
// int f[M][M]; // f[i][j] 前i个数中选择若干个物品，并且其体积之和小于等于j的最大价值
int f[M];   // 优化后将f[i][j]变为一维数组f[j], 其中j为体积

int main()
{
    int n , m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) // 下标从1开始
    {
        cin >> v[i] >> w[i];
    }
    
    for (int i = 1; i <= n; i ++ )
    {
        for(int j = m; j >= 0; j--)
        {
            // f[i][j] = f[i - 1][j]; // 不选择第i个物品
            // 优化后 f[j] = f[j];
            if(j >= v[i]) // 当j >= v[i] 时，才能选择第i个物品
            {
                // f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); // 不选择第i个物品和，选择第i个物品做对比
                f[j] = max(f[j], f[j - v[i]] + w[i]); // 将j从大到小遍历，算出的f[j - v[i]], 即为i-1得时候的f[j - v[i]]，
                                                      //因为此时f[j - v[i]]尚未被赋值
            }
        }
        // 发现f[i][j]的第一维,可以优化掉
    }
    cout << f[m] << endl;
    return 0;
}

3.完全背包

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
// 完全背包问题和0,1背包问题的区别，完全背包问题的选择问题可以分为不选、选1个、选2个、选3个.....选n个等
int f[N][N]; // f[i][j] 为在i个种类中，选择容量小于等于j的最大价值
int v[N], w[N];
int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j++)
            f[i][j] = f[i - 1][j];
            if(j >= v[i])
                f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]); // 与01背包不同点就在于01背包为f[i-1][j-vi] + w[i], 而完全背包为f[i][j - v[i]] + w[i];
    
    // 优化后j的遍历顺序从小到大，不需要和01背包一样从大到小遍历。。。
    cout << f[n][m];
    return 0;
}

4 多重背包问题

• 朴素算法

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 110;
int f[N][N];
//f[i][j]含义同01背包和完全背包问题，即选择前i个物品，体积不大于j的最大价值
int v[N], w[N], s[N];
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ )
    {
        cin >> v[i] >> w[i] >> s[i];   
    }   
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            for(int k = 0; k <= s[i]; k++)
            {
                // f[i][j] = f[i-1][j];
                // 不能写f[i][j] = f[i-1][j]，
                //因为多重背包问题考虑了不选择第i个物品的情况后，如果j>=k*v[i],并且选择了选若干个第i个物品的情况；
                //第二次在进行f[i][j] = f[i-1][j]会将最大值给覆盖掉
                if(j >= k * v[i])
                    f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
    cout << f[n][m];
    return 0;
}

• 优化后的算法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2021;
const int M = 12010;
// 将每个物品的数量s优化为 1， 2， 4， 8, ...等多个包，每个都可以选择或者不选择,排列组合起来能够得到s的值
//log2000  < 11,取12，与N相乘取M==12010；
int f[N];
int v[M], w[M];
int main()
{
    int n, m;
    cin >> n >> m;
    int cnt = 0; //此时cnt相当于包含了i*s的所有数据的所以，相当于01背包的n
    for (int i = 1; i <= n; i ++ )
    {    
        int a, b, s;
        cin >> a >> b >> s;
        for(int k = 1; k <= s; k *= 2) // 优化操作
        {
            cnt++;
            s -= k;
            v[cnt] = k * a;
            w[cnt] = k * b;
        }
        if(s)
        {
            cnt++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }
    }    
    n = cnt; // 将cnt的值传递给n，确保能够计算到所有情况
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);     
    cout << f[m];
    return 0;
}

9. 分组背包

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110;
int v[N][N], w[N][N];
int s[N]; // s[i] 为第i组的物品数量
int f[N]; // f[i][j] ---> f[j]，省去第一维，f[i][j]代表前i组，体积不大于j的最大价值
// 分组背包同多重背包不同：多重背包是选择第i个物品选k个，而分组背包是选择第i组物品中的第k个
int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++)
            cin >> v[i][j] >> w[i][j];
    }
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= 0; j--)
            for(int k = 1; k <= s[i]; k++)
                if(j >= v[i][k])
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m];
    return 0;
}

线性DP

898. 数字三角形

• 像求路径这种线性问题，一般都是将状态表示表示为路径坐标，如f[i][j]，同时要考虑边界问题。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int f[N][N], w[N][N]; //f[i][j] 表示从底层到(i,j)的路径最大值，w[i][j]，表示(i,j)的值
//本题从底层向上计算路径最大值，避免一些边界问题
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            cin >> w[i][j];

    for(int i = 1; i <= n; i++) f[n][i] = w[n][i]; // 将最后一层的数赋值给f[][];
    for(int i = n; i; i --)
        for(int j = 1; j <= i; j ++)
            f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + w[i][j];
            
    cout << f[1][1]; 
    return 0;
}

895. 最长上升序列

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N];//状态表示
int p[N];//输入整数
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
        cin >> p[i];
    f[1] = 1;
    for(int i = 1; i <= n; i++) // 
    {
        f[i] = 1;
        for(int j = 1; j <= i; j++)
        {
            if(p[i] > p[j]) //如果p[i] > p[j]，证明存在比f[j]更大的单调递增子序列，但是不一定f[j]+1和f[i]的值谁大谁小
                f[i] = max(f[i], f[j] + 1);
        }
    }
    int res = 0;
    for(int i = 1; i <= n; i++) res = max(res, f[i]);
    cout << res;
    return 0;
}

896. 最长上升序列

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int q[N]; // q数组存入输入序列
int a[N]; // a[i] = j, 表示最大上升子序列长度为i的最后一个数为j
int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++)
        cin >> q[i];
    
    int cnt = 0; // 表示最大上升子序列的长度
    for(int i = 0; i < n; i++) // 在a[cnt]数组中寻找此时q[i]所在的位置，如果比所有的a[i]都大，证明cnt需要增加，要是比某个数小，则需要将q[i]替换a[]
    {
        int l = 0, r = cnt;
        while(l < r)
        {
            int mid = (l + r + 1) / 2;
            if(q[i] > a[mid]) l = mid;
            else r = mid - 1;
        }
        cnt = max(cnt, r + 1); // 如果 r+1大于cnt，证明r+1比a的长度长--q[i]大于a[cnt]，所以将cnt更新
        a[r + 1] = q[i];//将表示最大上升子序列长度为r+1的最后一个数更新为q[i]
    }
    cout << cnt;
    
    return 0;
}

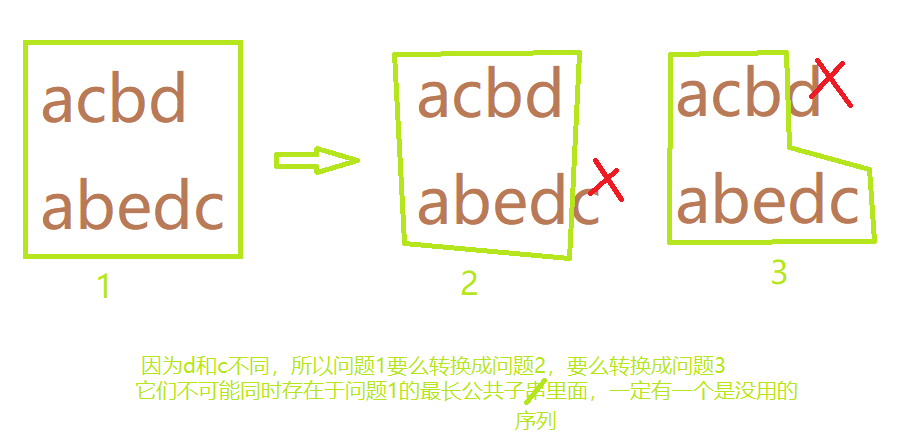
897.最长公共子序列

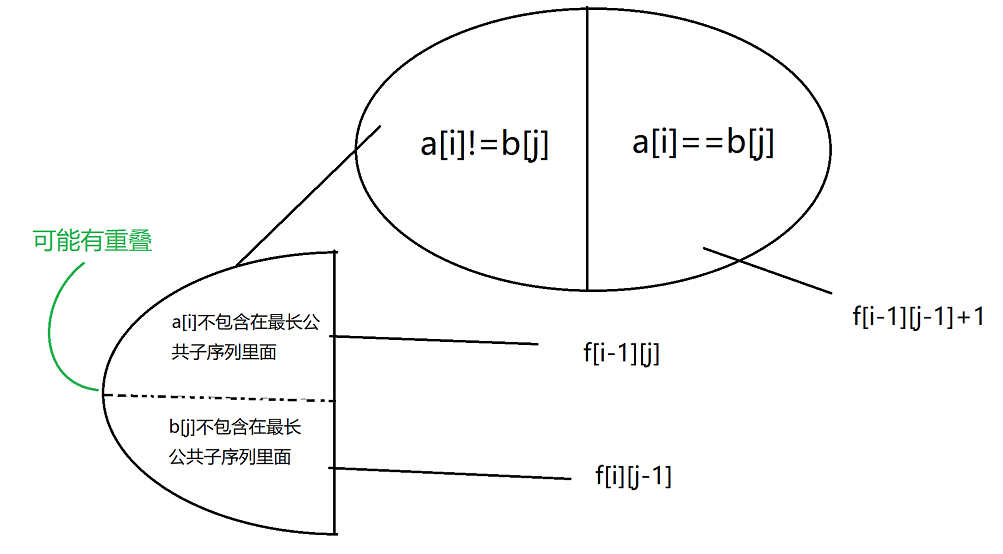
如果两个字符相等，就可以直接转移到f[i-1][j-1]，不相等的话，两个字符一定有一个可以抛弃，可以对f[i-1][j],f[i][j-1]两种状态取max来转移

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N]; // f[i][j]表示长度为i和j的字符串A和B的最大公共子序列
char a[N], b[N];// a,b为两个数组
int main()
{
    int n, m;
    cin >> n >> m >> a + 1 >> b + 1;
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = max(f[i-1][j],f[i][j-1]);
            if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i-1][j-1] + 1);
        }
    }
    cout << f[n][m];
    return 0;
}

902.最短编辑距离

状态表示 dp[i][j]
    集合 ： 所有吧a中的前i个字母 变成 b中前j个字母的集合的操作集合
    属性 ： 所有操作中操作次数最少的方案的操作数
状态计算
状态划分 以对a中的第i个字母操作不同划分
    在该字母之后添加
        添加一个字母之后变得相同，说明没有添加前a的前i个已经和b的前j-1个已经相同
        即 ： dp[i][j] = dp[i][j-1] + 1
    删除该字母
        删除该字母之后变得相同，说明没有删除前a中前i-1已经和b的前j个已经相同
        即 ： dp[i][j] = dp[i-1][j] + 1
    替换该字母
        替换说明对应结尾字母不同，则看倒数第二个
        即： dp[i][j] = dp[i-1][j-1] + 1
    啥也不做
        对应结尾字母相同，直接比较倒数第二个
        即： dp[i][j] = dp[i-1][j-1]

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N]; // f[i][j]为状态表示，表示第一个数组前i个数和第二个数组前j个数的最少操作次数
int main()
{
    cin >> n >> a + 1 >> m >> b + 1;
    
    for (int i = 1; i <= n; i ++ ) f[i][0] = i; // 当第二个数组为空的时候，删除第一个数组需要进行的步骤
    for (int i = 1; i <= m; i ++ ) f[0][i] = i; // 当第一个数组为空的时候，增加第一个数组需要进行的步骤
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = min(f[i-1][j], f[i][j-1]) + 1; // f[i-1][j] 为需要删除a[i]的状态，f[i][j-1] 为需要增加a[i]的状态
            
            f[i][j] = min(f[i][j], f[i-1][j-1] + (a[i] != b[j])); // f[i-1][j-1] + 1为a[i] != b[j],需要修改a[i]的情况; f[i-1][j-1]为a[i]=b[j]的情况
        }
    }
    cout << f[n][m];
    return 0;
}

899. 编辑距离

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
const int M = 11;
char a[N][M]; // 输入的字符串
int distance(char a[], char b[])
{
    int f[N][M]; // 状态表示
    int la = strlen(a + 1);
    int lb = strlen(b + 1);
    
    for(int i = 1; i <= la; i++) f[i][0] = i; // 删除操作
    for(int i = 1; i <= lb; i++) f[0][i] = i; // 增加操作
    
    for(int i = 1; i <= la; i++)
        for(int j = 1; j <= lb; j++)
        {
            f[i][j] = min(f[i-1][j], f[i][j-1]) + 1; // f[i-1][j]是删除a[i],f[i][j-1]是增加a[i];
            f[i][j] = min(f[i][j], f[i-1][j-1] + (a[i] != b[j])); // 如果a[i] = b[j], f[i-1][j-1] = f[i][j], 如果不等于就加一
        }
        return f[la][lb];
}

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        cin >> a[i] + 1;
    
    while(m--)
    {
        int q; // 操作限制
        char b[M]; // 查询字符串
        cin >> b + 1 >> q;
        
        int res = 0; // 达到要求的字符串数量
        for(int i = 1; i <= n; i++)
        {
            int d = distance(a[i], b);
            if(d <= q) res++;
        }
        cout << res << endl;
    }   
    return 0;
}

区间DP

282.石子合并

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 310;
int s[N]; // 前缀和
int f[N][N]; // f[i][j]表示从索引从i到j石子合并所需的最小代价
int a[N]; // 每一堆石子代价
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        s[i] = s[i-1] + a[i];
    }
    
    for(int len = 2; len <= n; len++) // 石子长度:最外围
    {
        for(int i = 1; i + len - 1 <= n; i++)
        {
            int l = i, r = i + len - 1; //l为开始索引，r为结束索引
            f[l][r] = 1e9;//设置一个比较大的值
            for(int j = l; j <= r; j++)
            {
                //将石子分为两堆，发现这两堆的计算最小代价没有关联。
                //所以就将f[l][r]与这两堆的最小代价+s[r] - s[l-1]相比较
                f[l][r] = min(f[l][r], f[l][j] + f[j + 1][r] + s[r] - s[l-1]);
            }
        }
    }
    cout << f[1][n];
    return 0;
}

计数类DP

900. 整数划分

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int mod = 1e9 + 7;
// 本题可以看成一个完全背包问题
const int N = 1010;
int f[N][N]; // 状态表示：f[i][j]表示从整数1-i中选择的对整数j的划分的数量

int main()
{
    int n;
    cin >> n;
    
    for(int i = 0; i <= n; i++) f[i][0] = 1;
    
    for(int i =1; i<= n; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            // f[i-1][j]表示不选择整数i，组合成j的总划分数量
            // f[i][j-i]表示选择整数i,但是
            f[i][j] = f[i-1][j] % mod;
            if(j >= i)
                f[i][j] = (f[i-1][j] + f[i][j-i]) % mod;
        }
    }
    cout << f[n][n];
    return 0;
}

状态压缩DP

91. 最短Hamilton路径

• 时间复杂度2^n*n2

• #include <iostream>
  #include <cstring>
  #include <algorithm>
  using namespace std;
  const int N = 20;
  const int M = 1 << 20; // M 表示一共有M条路径，路径使用二进制来表。0表示没有经过，1表示经过
  int f[M][N]; //状态表示f[i][j]表示从0到j，一共有i条Hamilton路径，最短hamilton路径
  int w[N][N];
  int main()
  {
      int n;
      cin >> n;
      for(int i = 0; i < n; i++)
          for(int j = 0; j < n; j++)
              cin >> w[i][j];
      memset(f, 0x3f, sizeof f);   
      f[1][0] = 0; //表示从0到0，有一条路径
      
      for(int i = 0; i < 1 << n; i++) // 一共有1<<n个状态路径
          for(int j = 0; j < n; j++) // j表示走到那个点
              if(i>>j&1) //表示i经过j，进行状态转移
                  for(int k = 0; k < n; k++) // k表示到j点途中经过k点
                      if(i>>k&1) //表示经过k , 因为hamilton路径必须是经过每一个点的路径，
                                 //所以经过k的路径进行状态转移，不经过的不需要进行状态转移
                          f[i][j] = min(f[i][j], f[i - (1<<j)][k] + w[k][j]); //状态转移含义：
                                                                              //表示途径k点，再由k点到达j的最小Hamilton路径
      cout << f[(1<<n) - 1][n-1];
      return 0;
  }
  

树形DP

285. 没有上司的舞会

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 6010;
int H[N]; // 开心指数
int f[N][2]; // 状态表示，f[i][0]表示选择不选择i时的最大快乐指数，f[i][1]表示选择i时的最大快乐指数
int h[N], idx, e[N], ne[N]; // 构建邻接表来表示身份树，根节点是最高的上司，依次向下
bool Father[N]; // Father[i]表示节点i有没有父亲节点
void add(int a, int b)  // 添加一条边a->b
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u) //遍历u的所有子节点
{
    f[u][1] = H[u]; // 先为f[u][1]赋值
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i]; //j为子节点的值
        dfs(j); //先进行深度优先遍历，就算出叶子节点的快乐值，然后依次向上计算
        f[u][1] += f[j][0];   // 状态计算分两种情况：1. 选择父节点，所以子节点都不能选择，将所有不选择子节点的快乐指数相加
        f[u][0] += max(f[j][0], f[j][1]);  // 2. 不选择父节点，所以子节点可以选择也可以不选择，进行比较选最大值，并将所有子节点快乐指数相加
    }
}
int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++)
        cin >> H[i];      
    memset(h, -1, sizeof h); // 将邻接表初始化为以-1为终止节点
    for (int i = 1; i <= n - 1; i ++ )
    {
        int a, b;
        cin >> a >> b;
        Father[a] = true;
        add(b, a);
    }
    int root = 0; // 将根节点初始化为0
    for(int i = 1; i <= n; i++)  // 查询根节点
        if(Father[i] == false)
        {
            root = i;
            break;
        }
    dfs(root);   
    cout << max(f[root][0], f[root][1]);
    return 0;
}

记忆化搜索

901. 滑雪

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 310;
int f[N][N]; // 状态表示：f[i][j]表示为从（i，j）出发一共有多少路径，状态属性：求最大值
//状态计算：一共有4个方向可以走：上下左右
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
int w[N][N]; // 每个区域的高度
int n, m;

int dp(int px, int py)
{
    if(f[px][py] != -1) return f[px][py]; // 优化操作，表明f[px][py]已经计算过可以直接返回
    f[px][py] = 1;
    for(int i = 0; i < 4; i++)
    {
        int x = px + dx[i];
        int y = py + dy[i];
        if(x >= 1 && x <= n && y >= 1 && y <= m)
        {
            if(w[x][y] < w[px][py])
            {    
                f[px][py] = max(f[px][py], dp(x,y) + 1);
                
            }
        }
    }
   
    return f[px][py];
}
int main()
{    
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin >> w[i][j];
    int res = 0;   
    memset(f, -1, sizeof f); // 将状态表示初始化为-1 ，表明没有经过任何计算
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j++)
            res = max(dp(i, j), res);         
    cout << res;
    return 0;
}