精度计算——乘法(大数乘大数)
摘自一个 ACM函数模板 ,学习记录自己的理解(^U^)ノ~YO
语法:mult(char a[], char b[], char ans[]);
参数:
a[]:被乘数,用字符串表示,位数不限
b[]:乘数,用字符串表示,位数不限
ans[]:结果,用字符串表示
返回值:null
注意:
-
空间复杂度为 o(n^2)
-
需要 string.h
源程序:
void mult(char a[], char b[], char ans[])
{
int res[200][200]={0};
int alen = strlen(a);
int blen = strlen(b);
char result[200];
int sum=0;
for(int i=0; i<alen; i++)
{
for(int j=0; j<blen; j++)
{
res[i][j]=(a[i]-'0')*(b[j]-'0');
}
}
int k=0; //结果的位数,从个位开始
//模拟乘法运算
for(int i=alen-1; i>=0; i--) //只求了alen位的低位结果,还有blen-1位没计算
{
for(int j=blen-1; j>=0; j--)
sum += res[i+(blen-1)-j][j]; //向左下方求和
result[k]=sum%10;
k++; //进一位
sum = sum/10;
}
for(int i=(blen-1)-1; i>=0; i--) //计算blen-1位高位结果
{
for(int j=0; j<=i; j++)
sum += res[i-j][j]; //向右上方求和
result[k]=sum%10;
k++;
sum = sum/10;
}
if(sum!=0) //最高位还有进位
{
result[k]=sum;
k++;
}
for(int i=0; i<k; i++) //并将内容回复成数字<0-9>
result[i] +='0';
for(int i=0; i<k; i++)
ans[i] = result[k-i-1];
ans[k]='\0';
while(true) //去除结果中的前导0
{
if(strlen(ans)!=1 && ans[0]=='0')
strcpy(ans,ans+1);
else
break;
}
}
理解:例 123x21
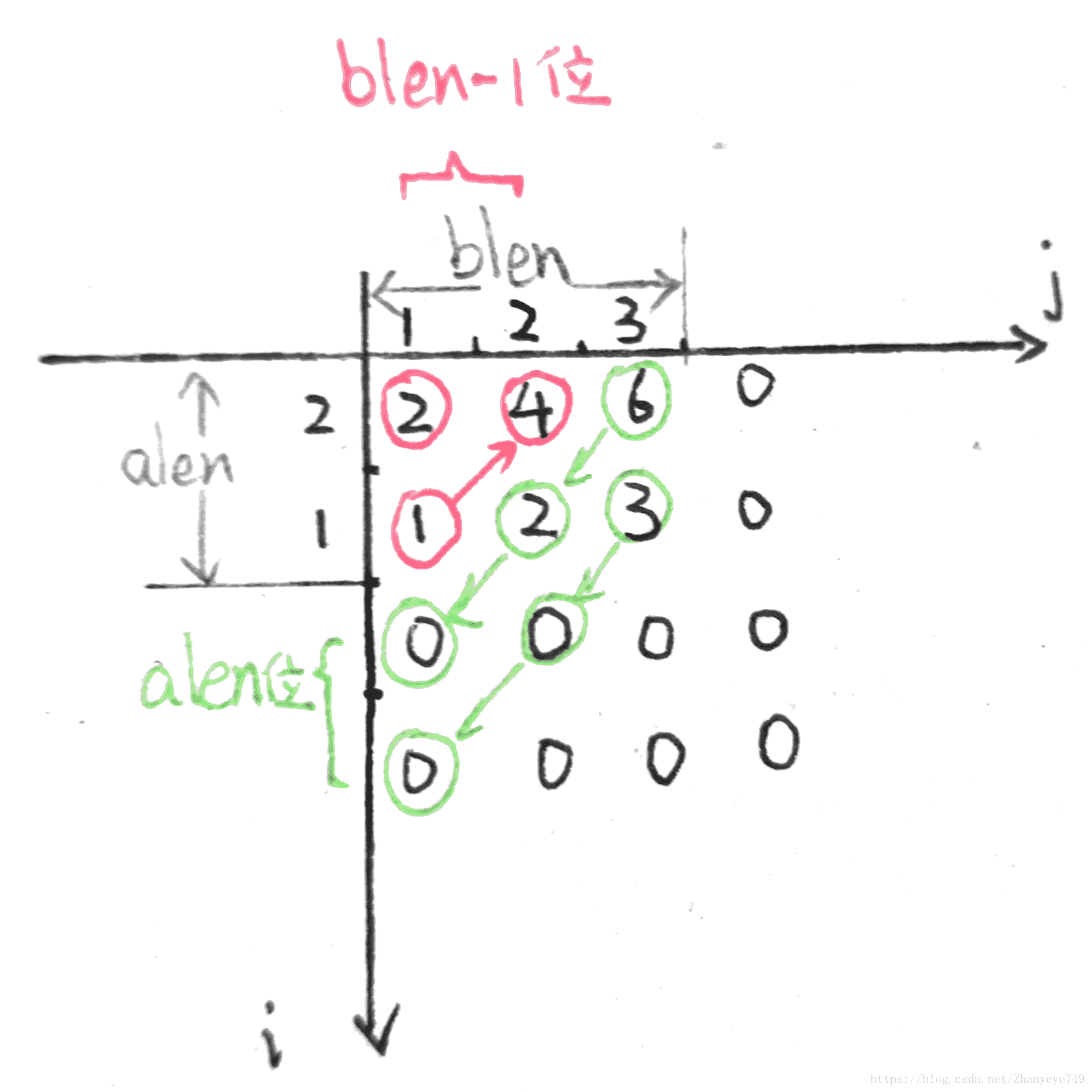










 本文深入探讨了一种处理大数乘法的高效算法,通过使用字符串表示任意长度的数字,实现了不受限于整型变量大小限制的乘法运算。算法采用二维数组存储中间结果,再进行累加得到最终结果,有效解决了大数运算问题。
本文深入探讨了一种处理大数乘法的高效算法,通过使用字符串表示任意长度的数字,实现了不受限于整型变量大小限制的乘法运算。算法采用二维数组存储中间结果,再进行累加得到最终结果,有效解决了大数运算问题。
















 4147
4147

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








