2.后根遍历:先依次后根遍历子树,再访问树的根节点。
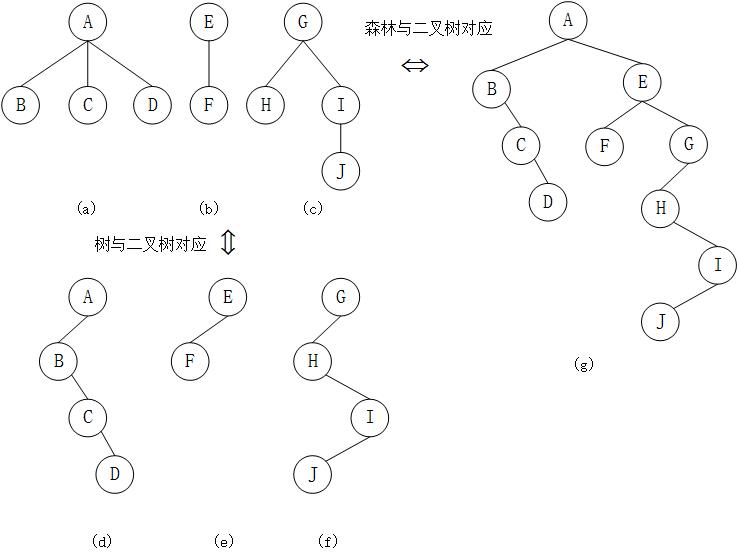
树的先根遍历和后根遍历可分别借用对应二叉树的先序遍历和中序遍历实现。以上图(a)中的树和其对应的(d)中的二叉树为例:
对树进行先根遍历:A B C D
对二叉树进行先序遍历:A B C D(与树的先根遍历一致)
(1)访问森林中第一棵树的根节点;
(2)先序遍历第一棵树中根节点的子树森林;
2.中序遍历森林
(1)中序遍历森林中第一棵树的根节点的子树森林;
(2)访问第一棵树的根节点;
(3)中序遍历除去第一棵树之后剩余的树构成的森林。
在森林的中序遍历方法中需要注意,森林的中序遍历与二叉树的中序遍历方法的定义不同,二叉树的中序遍历是按照LDR的顺序进行遍历,而森林的中序遍历是要先中序遍历第一棵树的所有子树,再访问这棵树的根节点,对于这棵树来说,根节点的访问次序其实是整棵树遍历的最后(类似于二叉树的后序),这里经常与二叉树的中序遍历混淆,傻傻分不清楚~
下面,看看森林遍历方法和其对应的二叉树遍历方法的对应关系。当森林转换成二叉树时,其第一棵树的子树森林转换成左子树,剩余树的森林转换成右子树,则森林的先序和中序遍历即对应二叉树的先序和中序遍历。以上图中(a)(b)(c)构成的森林和对应的二叉树(g)为例:
对森林进行先序遍历:A B C D E F G H I J
对森林进行中序遍历:B C D A F E H J I G
























 819
819

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








