机器学习day6:线性回归

可以尝试使用Kaggle上最新的“House Prices - Advanced Regression Techniques”数据集进行线性回归练习。这个数据集包含了房屋的各种特征（如面积、房间数、建造年份等）和对应的房屋价格。你可以使用matplotlib、numpy和Pandas来处理数据，并搭建一个线性回归模型来预测房屋价格。

‌题目‌：

1. 从Kaggle的“House Prices - Advanced Regression Techniques”数据集
2. 使用Pandas读取数据，并查看数据的基本信息。
3. 选择一些你认为对房屋价格有重要影响的特征，并进行数据预处理（如缺失值处理、异常值处理等）。
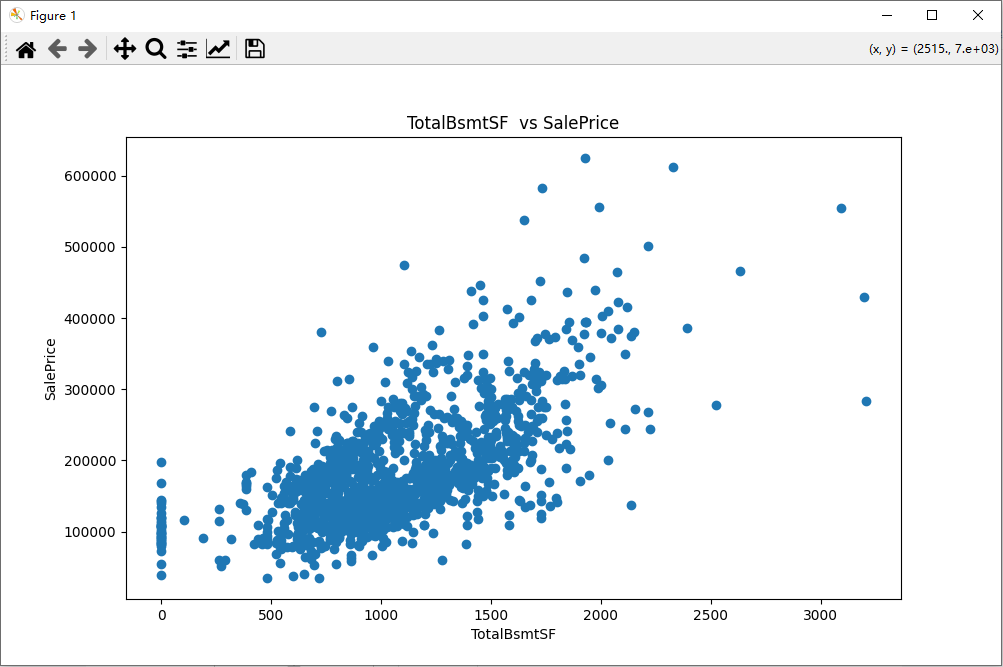
4. 使用matplotlib绘制特征与目标变量（房屋价格）之间的散点图或箱线图，观察它们之间的关系。
5. 将数据分为训练集和测试集。
6. 使用numpy或scikit-learn搭建一个线性回归模型，并在训练集上进行训练。
7. 在测试集上评估模型的性能，并计算均方误差（MSE）或均方根误差（RMSE）。
8. 尝试使用不同的特征组合或进行特征选择，观察模型性能的变化。

   import pandas as pd
   import numpy as np
   import matplotlib.pyplot as plt
   from sklearn.model_selection import train_test_split
   from sklearn.linear_model import LinearRegression
   from sklearn.metrics import mean_squared_error
   
   # 1. 从Kaggle的“House Prices - Advanced Regression Techniques”数据集
   train_data = pd.read_csv('train.csv')
   test_data = pd.read_csv('test.csv')
   
   # 2. 使用Pandas读取数据，并查看数据的基本信息 
   print("训练集基本信息：")
   train_data.info()
   
   # 3. 选择一些你认为对房屋价格有重要影响的特征，并进行数据预处理 
   # 选择特征 
   selected_features = ['OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'YearBuilt']
   target = 'SalePrice'
   
   # 处理训练集缺失值 
   train_data[selected_features] = train_data[selected_features].fillna(train_data[selected_features].mean())
   
   # 处理异常值
   train_data = train_data[train_data['GrLivArea'] < 4000]
   
   # 4. 使用matplotlib绘制特征与目标变量（房屋价格）之间的散点图或箱线图 
   for feature in selected_features:
       plt.figure(figsize=(10, 6))
       plt.scatter(train_data[feature], train_data[target])
       plt.xlabel(feature)
       plt.ylabel(target)
       plt.title(f'{feature}  vs {target}')
       plt.show()
   
   # 5. 将数据分为训练集和测试集 
   X = train_data[selected_features]
   y = train_data[target]
   X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
   
   # 6. 使用numpy或scikit-learn搭建一个线性回归模型，并在训练集上进行训练 
   model = LinearRegression()
   model.fit(X_train, y_train)
   
   # 7. 在测试集上评估模型的性能，并计算均方误差（MSE）或均方根误差（RMSE） 
   y_pred = model.predict(X_test)
   mse = mean_squared_error(y_test, y_pred)
   rmse = np.sqrt(mse)
   print(f"均方误差 (MSE): {mse}")
   print(f"均方根误差 (RMSE): {rmse}")
   
   # 8. 尝试使用不同的特征组合或进行特征选择，观察模型性能的变化 
   # 选择新的特征组合 
   new_features = ['OverallQual', 'GrLivArea', 'GarageArea', 'TotalBsmtSF', 'YearBuilt', 'FullBath']
   X_new = train_data[new_features]
   X_new = X_new.fillna(X_new.mean())
   
   X_train_new, X_test_new, y_train_new, y_test_new = train_test_split(X_new, y, test_size=0.2, random_state=42)
   
   model_new = LinearRegression()
   model_new.fit(X_train_new, y_train_new)
   
   y_pred_new = model_new.predict(X_test_new)
   mse_new = mean_squared_error(y_test_new, y_pred_new)
   rmse_new = np.sqrt(mse_new)
   print(f"新特征组合的均方误差 (MSE): {mse_new}")
   print(f"新特征组合的均方根误差 (RMSE): {rmse_new}")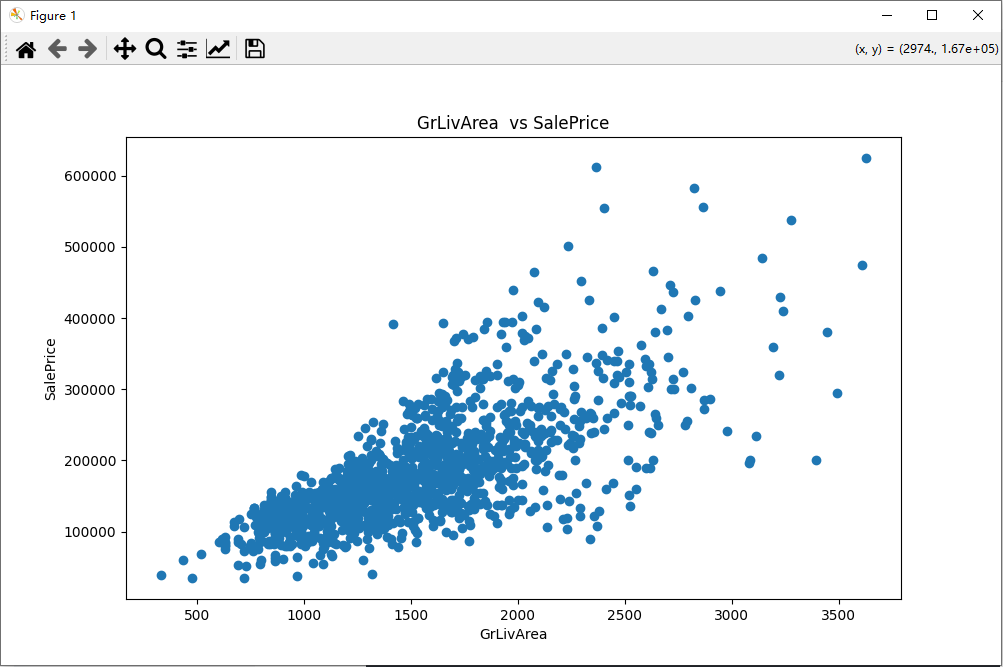 

   运行代码：