图的存储结构

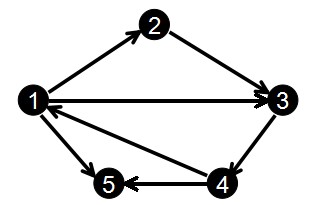
图为G（V，E）。 V代表点集，E代表边集。n为点的个数，m为边的个数。

下面代码基于这个图：

五个点七条边。

输入边的顺序为：

起点，终点，边权

1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7

图片和数据来自：深度理解链式前向星

邻接矩阵：

对于邻接矩阵来说，初始化所有边权为极大值INF，需要的时间，建图需要O（m），所以总的时间复杂度是。空间上，邻接矩阵的开销也是，与点的个数有关。

优点：可以直接查询到是否有边，如果有边权为多少。

缺点：空间开销大，遍历速度慢。

一般用于稠密图，或顶点较少的图。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;//点数最大值
const int MAXM = 1005;//边数最大值
const int INF = 0x3f3f3f3f;
int n, m;//n个点，m条边
int G[MAXN][MAXN];//G[i][j] = w;表示i到j有一条边权为w的边
int main()
{
    cin >> n >> m;
    int from, to, w;
    memset(G, INF, sizeof(G));
    for (int i = 1; i <= m; i++)
    {
        cin >> from >> to >> w;
        G[from][to] = w;
    }
    for (int i = 1; i <= n; i++)
    {
        cout << i << endl;
        for (int j = 1; j <= n; j++)
        {
            if (G[i][j] != INF) cout << i << " " << j << " " << G[i][j] << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
*/

前向星

因为需要对边集数组排序，一般情况下时间复杂度为。空间上，需要两个数组，所以空间复杂度为。遍历复杂度为O（m）。

优点：可以应对点非常多的情况，可以存储重边。

缺点：判断两个顶点和之间是否有边效率低。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;//点数最大值
const int MAXM = 1005;//边数最大值
int n, m;//n个点，m条边
struct Edge
{
    int from ,to, w;//起点,终点,边权
    bool operator < (const Edge& a) const
    {
        if(from != a.from) return from < a.from;
        if(to != a.to) return to < a.to;
        return w < a.w;
    }
}edge[MAXM];//边集
int head[MAXN];//head[i],表示以i为起点的第一条边在边集数组的位置
int main()
{
    cin >> n >> m;
    int from;
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> edge[i].from >> edge[i].to >> edge[i].w;//加边
    }
    sort(edge, edge + m);//以起点升序排序
    memset(head, -1, sizeof(head));//初始化
    head[edge[1].from] = 1;
    for (int i = 2; i <= m; i++)//确定head[i],表示以i为起点的第一条边在边集数组的位置
    {
        if(edge[i].from != edge[i - 1].from) head[edge[i].from] = i;
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for (int j = head[i]; edge[j].from == i && j <= m; j++)//遍历以i为起点的边
        {
            cout << edge[j].from << " " << edge[j].to << " " << edge[j].w << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
*/

邻接表：

①动态建表：

动态建立的邻接表，时间效率为O（m），空间效率也为O（m）。遍历效率也为O（m）。

优点：时间效率和空间效率都比较高。

缺点：需要随着加边申请内存，直接判断两个顶点和之间是否有边效率低。

由于代码不太好写，所以比赛中用的较少。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;//点数最大值
const int MAXM = 1005;//边数最大值
const int INF = 0x3f3f3f3f;
int n, m;//n个点，m条边
struct EdgeNode//邻接表节点
{
    int to, w;//终点,边权
    EdgeNode *Next;//指向下一条边的指针
};
struct VNode//起点表节点
{
    int from;//起点
    EdgeNode *first;//邻接表头指针
};
VNode head[MAXN];//整个图的邻接表（头指针）
void add_edge(int from, int to, int w)
{
    EdgeNode *p = new EdgeNode;
    p->to = to;
    p->w = w;
    p->Next = head[from].first;
    head[from].first = p;
}
int main()
{
    cin >> n >> m;
    int from, to, w;
    for (int i = 1; i <= m; i++)
    {
        cin >> from >> to >> w;
        add_edge(from, to, w);//加边
    }
    for (int i = 1; i <= n; i++)
    {
        cout << i << endl;
        for (EdgeNode *j = head[i].first; j != nullptr; j = j->Next)
        {
            cout << i << " " << j->to << " " << j->w << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
*/

②vector实现邻接表：

复杂度和邻接表基本一样。代码少不容易犯错误，内存的申请和释放都不需要自己处理。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;//点数最大值
const int MAXM = 1005;//边数最大值
int n, m;//n个点，m条边
struct Edge
{
    int to, w;//终点,边权
}e;
vector<Edge> edge[MAXM];//edge[i],表示以i为起点的边集
int main()
{
    cin >> n >> m;
    int from;
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> from >> e.to >> e.w;
        edge[from].push_back(e);//加边
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for (auto j: edge[i])//遍历以i为起点的边
        {
            cout << i << " " << j.to << " " << j.w << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
*/

极少情况下可能会出现内存超限，跟vector申请内存方式有关。

③链式前向星：

链式前向星其实就是静态建立的邻接表，时间效率为O（m），空间效率也为O（m）。遍历效率也为O（m）。

优点：时间效率和空间效率高。

缺点：直接判断两个顶点和之间是否有边效率低。

因为是一次性申请内存，所以比邻接表实时申请快一些。

可以说是目前建立图和遍历效率最高的存储方式。比赛中常用。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;//点数最大值
const int MAXM = 1005;//边数最大值
int n, m;//n个点，m条边
struct Edge
{
    int to, w, Next;//终点，边权，同起点的上一条边的编号
}edge[MAXM + 5];//边集
int head[MAXN + 5];//head[i],表示以i为起点的第一条边在边集数组的位置（编号）
void init()//初始化
{
    for (int i = 0; i <= n; i++) head[i] = -1;
}
void add_edge(int u, int v, int w, int i)//加边，u起点，v终点，w边权，i为边的编号
{
    edge[i].to = v;
    edge[i].w = w;
    edge[i].Next = head[u];//以u为起点上一条边的编号
    head[u] = i;//更新以u为起点上一条边的编号
}
int main()
{
    cin >> n >> m;
    int u, v, w;
    init();//初始化
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> u >> v >> w;
        add_edge(u, v, w, i);//加边
        /*
        加双向边
        add_edge(u, v, w, i * 2);
        add_edge(v, u, w, i * 2 + 1);
        */
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for (int j = head[i]; j != -1; j = edge[j].Next)//遍历以i为起点的边
        {
            cout << i << " " << edge[j].to << " " << edge[j].w << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
*/

除了这些，还有 邻接多重表， 多重边集数组， 十字链表等存图方式。