多分辨率展开-CSDN博客

本文链接：https://blog.csdn.net/a03910/article/details/138172332

本文讨论了Hilbert空间中的对偶基概念，特别是在C[a,b]和L2(R)函数空间的应用。作者指出书中的某些术语翻译错误，并分析了正交基、单位正交基的区别，以及MRA中的小波函数构造和相关数学概念，如闭子空间、完备性和内积的使用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.,首先这个图居然给出了基和对偶基相等这个概念。我需要说明一下这个概念的来源。

1.1.,对偶基一开始是来自高等代数的线性空间，然后是泛函分析中的赋范线性空间的共轭空间。至于基的概念，赋范线性空间并没有，可能是因为正交需要内积来定义，所以只有hilbert空间有直交系的概念，直交系跟基的概念差不多。这里对偶基都相等了，那只能是hilbert空间了。问题是这里的空间元素是什么函数？首先我只考虑连续复值函数空间C[a,b]，这是完备的赋范向量空间，然后定义内积就是hilbert空间了，那么情况1就好理解了。不过书上之后到底是用于离散函数呢？这个就不好说了。我看到了之后的内容后，发现书上的尺度函数属于L2(R)，而L2(R)是hilbert空间，那么以后就只看这个空间了。

1.2.,情况2的内容就是单位正交基和一般的正交基。但是书上说出成是正交和不和自身正交，这种说法如果不懂数学简直是胡说八道。我确信英文作者的数学基础不行，而翻译者的数学基础更不行。把dual翻译成了二重，应该是对偶。特别是前面的滤波器的taps翻译为插头简直是脑残。明显是表示节拍的拍。

1.2.1.,情况2说的基函数和对偶双正交，其实是线性空间和对偶空间的定义了，都不需要赋范就有的，更不需要内积了。没啥可以说的。

1.3.,情况3说的啥？不是V的基，但是支持展开。如何理解？实际上V是线性闭子空间，那就是写成了级数形式，而公式7.2.1已经超越了可列个数的和，而是不可列个数的和，居然还不是V的基。然后书上说是超完备的，冗余的，那就是确实是不可列个函数相加了。

但是还有个问题，要成为线性闭子空间，需要成为哪个内积空间的闭子空间？而且就算是闭子空间也不一定完备。书上完全没给出，看来是作者不懂瞎写了，抄没抄全。

1.3.1.,至于公式7.3.8第二个不等式是贝塞尔不等式。至于第一个不等式，是因为V中的任意元素f是展开集合中至多可列个组合(本来是有限个组合，但是变成闭包就是可列个了。)，所以展开集合其他的元素和f的内积平方>=0。实际上A=1,B=1。这里f属于V的时候是取等号的。因为作者不懂瞎写。

scaling function书上翻译为尺度函数，实际上应该翻译为缩放函数。

真是笑死我了，span L2(R)翻译解释为跨越，但是实际上在高等代数中符号span表示有限生成的意思。但是字面含义呢？确实是横跨，所以翻译失去了作者要表达的意图了，只能翻译为“扩张成”，生成。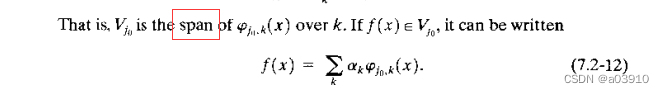

这里的span应该翻译为有限生成，或者扩张。

MRA是多分辨率分析。

measurable是可测的意思，但是翻译写成了度量。

这里的问题7.11的函数不是有效收缩函数？意思指的应该是满足MRA的条件2。不符合子空间套吗？

这只需要用一维表示即可。首先V0有效区间是[1/4+k,3/4+k)，V1的有效区间是[1/8+k/2,3/8+k/2)。发现这个区间无法用V1得到。那就是V0不包含于V1，所以不满足条件2.

MRA的条件3的common是共有的意思，翻译者翻译为通用的，错的离谱。

条件4说任意的勒贝格可测函数，且平方可积，那么可以使用极限表示？

这是真的吗？看起来是错误的结论，因为Vj只是在区间段有效的函数而已，无论区间段多么小，都是区间。但是好在是前闭后开区间，意味着极限可以是单个点。实际上有效区域都是勒贝格可测集。然后是需要一个函数能够在改变区间之后的可列次累加得到任何的平方可积函数，说实话，这个证明我就不会。存在这样的函数吗？当然存在，只要设为公式7.2-14的简单函数就会明显感觉到，这个函数确实能做到。因为在任意勒贝格可测集上，存在连续函数fn的极限为f，在勒贝格测度的意义下。对于每个连续函数fn，可以使用简单函数 $\varphi_{i}$ 逼近吗？我想到了积分过程，因为积分区间的值都是取一个点，那么这就是简单函数了。所以简单函数的极限和f只差一个零测集，这里是L2空间，所以那就是了。唯一的问题是平方可积，因为这里是可测函数是平方可积的，需要的也是简单函数的极限也是平方可积的，看起来也是合理的对应上了。简单函数并不一定可积，但是一定平方可积的。那我就证明了这里说的内容了。至少存在一个函数 $\varphi$ 使得按照书上的构造的方式，可以构造出来L2(R)中的函数。不是真的能构造出来，而是构造出来函数列fn，可以求极限逼近。

接下来是小波函数了，小波函数看起来和平方可积函数空间的定义一样。但是我观察了一下，发现在给定了伸缩函数之后，其实已经创建了子空间套Vi。然后寻找能够表达子空间Wi=V(i+1)-Vi，函数，叫做小波函数，如书上的公式7.2.20所示。这真的能找到吗？这是个数学证明题，看起来书上没有给出解释，我也不做证明了，我只是给出已给基本的分析。

首先线性空间相减，正交补，如何理解? Vj是完备的线性空间吗？因为L2(R)是完备的，他的闭子空间都是完备的，所以Vj是完备的。既然Vj是V(j+1)的完备子空间，那么有Vj $\perp$ $\bigoplus$ Vj=V(j+1)，其中Vj $\perp$ =V(j+1)-Vj，Vj $\perp$ 是Vj在V(j+1)的正交补。这些结论都是非常明显的，在泛函分析中甚至都没有明确说明，因为根据定义看很明显。

其实，非常明白，为什么使用L2R空间，因为定义内积的需要，使得根据内积产生的范数就是平方积分的，而范数的作用是成为度量空间之后可以求极限，获得闭集的概念，毕竟一开始是向量空间，而不是拓扑空间。

现在说Vj $\perp$ ,也就是空间Wj，首先肯定是能找到直交系的，我为什么要说成是直交系而不说成是正交基呢？因为正交基是有限生成的，这里是闭集，极限的元素不是有限生成的，直交系更合理，但是事实上偏微分方程中也是用了正交基来说明极限点的，我看的书不多不明白这里，只能认为改了定义，从有限生成改成了可列个生成的，但是绝对不会是任意组合的，因为根据直交系的内容会发现，直交系中的不可数个元素都和f的内积为0，这说明了基中使用不可数个元素表示空间中的某个元素的意义不大了。但是这个直交系的元素要满足公式7.2-19，这就难办了，因为需要正交基有平移的性质，这是我做不到的，但是别人完成了证明。

然后是我需要说明一点，Vj的j可以为负数，为正数是收缩了，为负数是伸长了。（但是说实话，这个对MRA要求的整数平移正交不利，目前注意到即可不管。）

as with和...一样

然后是书上说了一个问题，f0是V1的元素，而不是V0的，如果单纯的从基的角度看，只需要用W0中的元素表示即可，但是书上使用了V0的基元素的表示，这是不可能的，用了这个在W0中都无法消去了。所以是我理解错了。f0是V1的元素，而不是V0的元素的含义是f0不能被V0分解，只能被V1分解，其实是f0中含有V0的部分的意思，我以为是不属于就是完全不包含基的成分，但其实不是。理解这里需要注意一点，就是V1和V0的正交基中的元素完全不同，但是正交基在线性空间中是可以转换的，可以转换成包含关系，但是公式7.2-10就完全变样了。

所以f0不是V0的元素的含义是不能被V0中的基元素表示，但是肯定是可以使用V0里面的元素和V1的元素组合出来的，也可以直接使用V1的元素组合出来而不使用V0中的元素。