树状数组及应用

最新推荐文章于 2024-05-28 12:11:29 发布

lin..6

最新推荐文章于 2024-05-28 12:11:29 发布

阅读量919

点赞数 35

文章标签：算法数据结构 c++

本文链接：https://blog.csdn.net/a111737289291/article/details/137060719

版权

如果数列A是静态不变的，那么处理前缀和复杂度为O(n)，查询为O(1)，但如果序列是动态变化的，如改变其中一个元素，那么就需要重新计算前缀和，如果每次查询都有变化，那么复杂度会大幅度增加。

有两种数据结构可以高效的处理这个问题：树状数组与线段树。

1.树状数组的概念与基本编码

1.1.引导

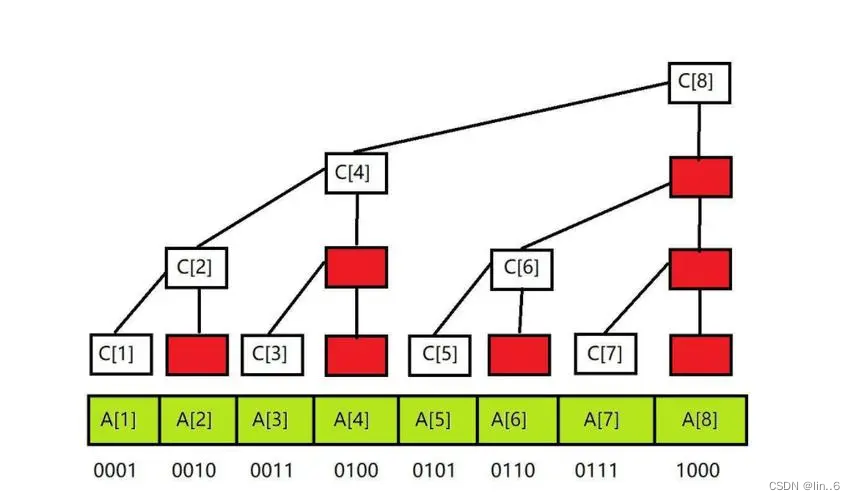
如图所示，c[1] = A[1], c[2] = c[1] + A[2], c[3] = A[3], c[4] = c[2] + c[3] + A[4], ... , c[8] = c[4] + c[6] + c[7] + A[8]。

利用c数组可以高效的完成以下两个操作。

（1）查询，即求前缀和sum。
（2）维护，即元素a发生变化时，能以O( $log_2(n)$ )的高效率修改c[] 的值。

结论：

（1）查询过程是每次去掉二进制的最后一个1。例如，求sum[7]：

sum[7] += c[7]
7的二进制是111，去掉最后一个1，得110，即c[6]，所以sum[7] += c[6]
110，去掉最后一个1，得100，sum[7] += c[4]
100，去掉最后一个1就没有了

故sum[7] = c[7] + c[6] + c[4]

（2）维护的过程是每次在二进制最后的1上加1。例如，更新a[3]：

3的二进制是11，在最后一个1上加1，得100，所以修改c[4]；
100，在最后一个1上加1，得1000，所以修改c[8]；
继续修改c[16]，c[32]...

树状数组的关键就是找到最后一个1。

1.2.lowbit(x)

lowbit(x) = x & (-x)，功能为找到x的二进制数最后一个1。其原理是利用负数的补码，例如x = 6 = 000110， $(-x)_{}$ 补 = 111010，那么x & (-x) = 10 = 2；

lowbit(x) 部分结果如下：

x	x的二进制	lowbit(x)	tree[x]数组
1	1	1	tree[1] = a1
2	10	2	tree[2] = a2 + a1
3	11	1	tree[3] = a3
4	100	4	tree[4] = a4 + a3+ a2+ a1
5	101	1	tree[5] = a5
6	110	2	tree[6] = a6 + a5
7	111	1	tree[7] = a7

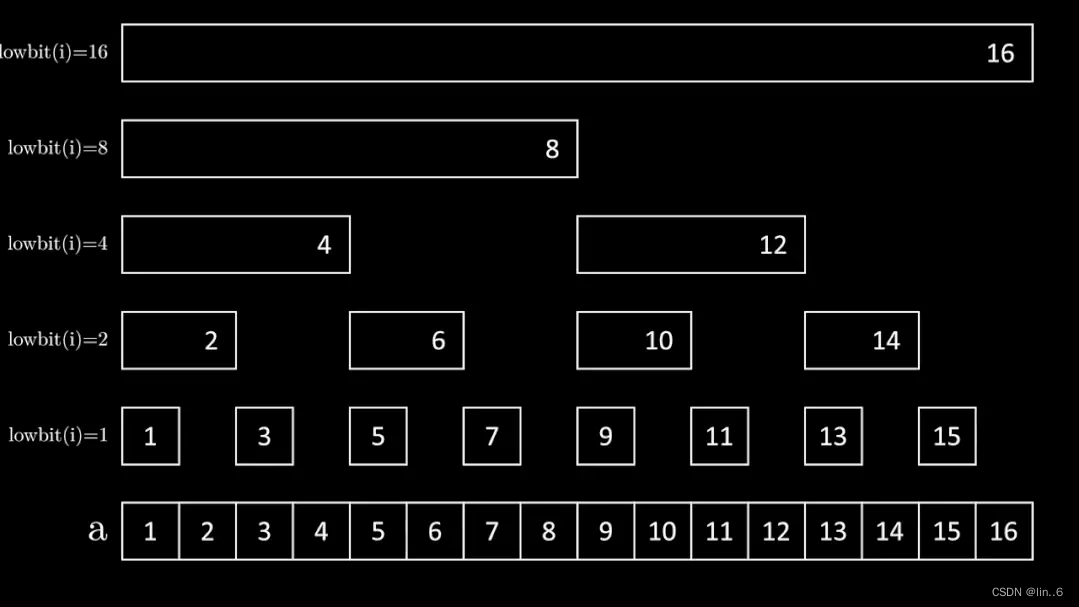
令m = lowbit(x)，tree[x]的值是把 $a_{x}$ 和他前面共m个数相加的结果。

tree[]数组是通过lowbit计算出的树状数组，它能够以二分的复杂度存储一个数列的数据，具体的说，tree[x]存储的是区间[x - lowbit(x) + 1, x]的每个数的和。

1.3.树状数组的编码

下面给出单点修改＋区间查询的代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) (x & (-x))
const int N = 1000;
int tree[N];
void update(int x, int d) {//单点修改，修改玄素a[x]，a[x] = a[x] + d
    while (x <= N) {
        tree[x] += d;
        x += lowbit(x);
    }
}
ll sum(int x) {//查询前缀和：返回前缀和sum = a[1] + a[2] + .., + a[x]
    ll ans = 0;
    while (x > 0) {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}
void solve() {
    int n;
    cin >> n;
    vector<ll> a(n + 1, 0);//a[0]不用
    memset(tree, 0, sizeof(tree));
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        update(i, a[i]);
    }
    //查询区间和：
    cout << "Old : sum([1,n-1]):" << sum(n - 1) - sum(0) << endl;
    //模拟一次修改,a[n-1] + 100
    update(n - 1, 100);
    cout << "New : sum([1,n-1]):" << sum(n - 1) - sum(0) << endl;
}
int main() {
    ios::sync_with_stdio;
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}
/*
输入：
10
4 5 6 7 8 9 10 11 12 13
输出：
Old : sum([1,n-1]):72
New : sum([1,n-1]):172
*/

此代码过程：

（1）初始化：先清空数组tree，然后读取a数组每一个元素，用update() 逐步处理这n个数，得到tree[]数组；
（2）求前缀和：用sum()计算，求和基于tree数组；
（3）单点修改：执行update()函数，修改数组tree[]。

2.树状数组的基本应用

2.1.单点修改＋区间查询

1.1.3.树状数组的编码已经给出

2.2.区间修改+单点查询

利用差分是前缀和的逆运算来求解

例题：

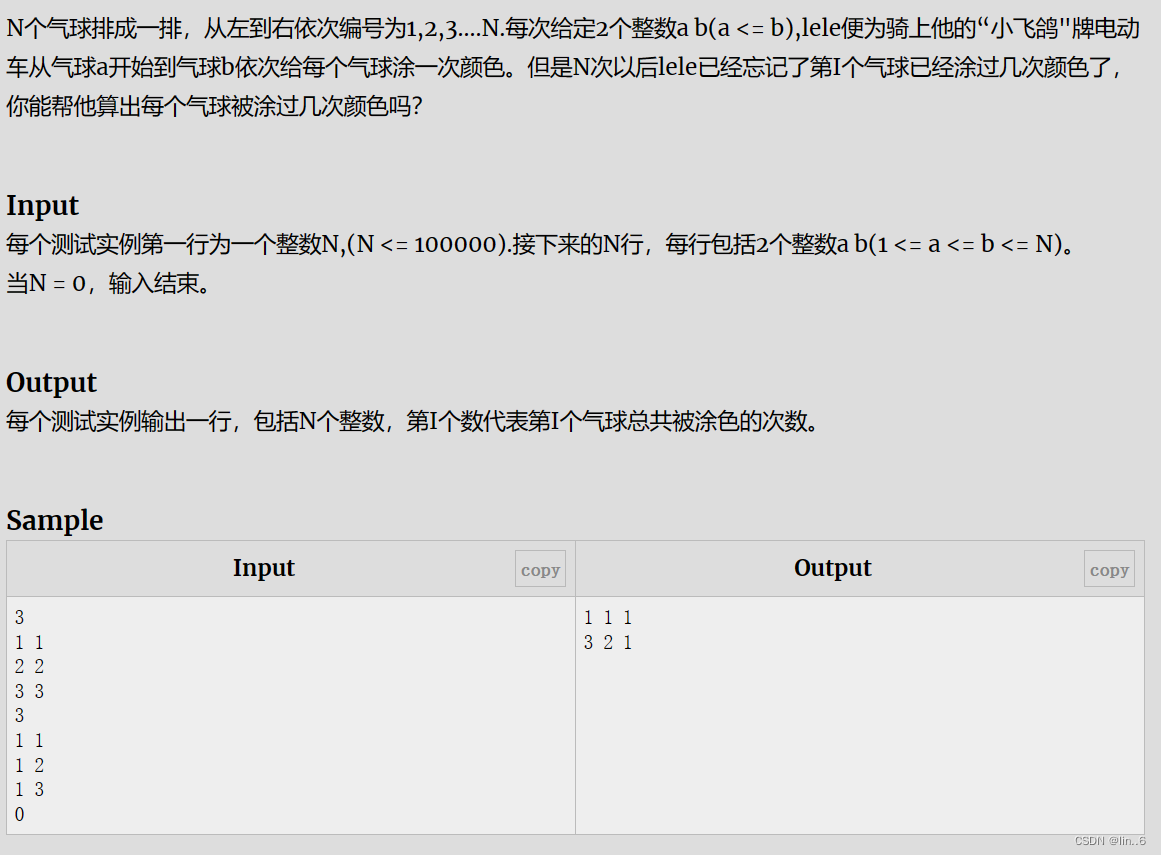
两种解法：

第一种，单纯的差分数组

#include<bits/stdc++.h>
using namespace std;
int n, a, b, diff[100002];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	while (cin >> n && n != 0) {
		for (int i = 0; i <= n; i++) {
			diff[i] = 0;
		}
		for (int i = 0; i < n; i++) {
			cin >> a >> b;
			diff[a] += 1;
			diff[b + 1] -= 1;
		}
		diff[1] += diff[0];
		cout << diff[1];
		for (int i = 2; i <= n; i++) {
			diff[i] += diff[i - 1];
			cout << ' ' << diff[i];
		}
	}
	return 0;
}

第二种，利用树状数组

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) (x & (-x))
const int N = 100010;
int tree[N];
void update(int x, int d) {
    while (x <= N) {
        tree[x] += d;
        x += lowbit(x);
    }
}
ll sum(int x) {
    ll ans = 0;
    while (x > 0) {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}
void solve() {
    int n;
    while (cin >> n && n != 0) {
        memset(tree, 0, sizeof(tree));
        for (int i = 1; i <= n; i++) {
            int L, R;
            cin >> L >> R;
            update(L, 1);
            update(R + 1, -1);
        }
        for (int i = 1; i <= n; i++) {
            if (i != n)cout << sum(i) << ' ';
            else cout << sum(i) << endl;
        }
    }
}
int main() {
    ios::sync_with_stdio;
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}

2.3.区间修改＋区间查询

完成区间修改需要一个tree，区间查询也需要一个tree，所以可以利用两个tree达成此要求

$a_{1}+a_{2}+...+a_{k - 1 }+a_{k}$
= $d_{1} + (d_{1}+d_{2}) +... + \sum_{i=1}^{k-1}d_{i}+\sum_{i=1}^{k}d_{i}$
= $k\sum_{i =1 }^{k}d_{i} - \sum_{i =1 }^{k}(i-1)d_{i}$

所以可以分别处理d和(i-1)d两个数组的树状数组

例题：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) (x & (-x))
const int N = 100010;
ll tree1[N], tree2[N];
void update1(ll x, ll d) {
    while (x <= N) {
        tree1[x] += d;
        x += lowbit(x);
    }
}
ll sum1(ll x) {
    ll ans = 0;
    while (x > 0) {
        ans += tree1[x];
        x -= lowbit(x);
    }
    return ans;
}
void update2(ll x, ll d) {
    while (x <= N) {
        tree2[x] += d;
        x += lowbit(x);
    }
}
ll sum2(ll x) {
    ll ans = 0;
    while (x > 0) {
        ans += tree2[x];
        x -= lowbit(x);
    }
    return ans;
}
void solve() {
    ll n, m;
    memset(tree1, 0, sizeof(tree1));
    memset(tree2, 0, sizeof(tree2));
    cin >> n >> m;
    ll old = 0, a;
    for (int i = 1; i <= n; i++) {
        cin >> a;
        update1(i, a - old);
        update2(i, (i - 1) * (a - old));
        old = a;
    }
    while (m--) {
        ll q, L, R, d;
        cin >> q;
        if (q == 1) {
            cin >> L >> R >> d;
            update1(L, d);
            update1(R + 1, -d);
            update2(L, (L - 1) * d);
            update2(R + 1, -R * d);
        }
        else {
            cin >> L >> R;
            cout << R * sum1(R) - sum2(R) - (L - 1) * sum1(L - 1) + sum2(L - 1) << endl;
        }
    }
}
int main() {
    ios::sync_with_stdio;
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}

lin..6

关注

35
点赞
踩
16

收藏

觉得还不错? 一键收藏
打赏
0
评论
树状数组及应用

如果数列A是静态不变的，那么处理前缀和复杂度为O(n)，查询为O(1)，但如果序列是动态变化的，如改变其中一个元素，那么就需要重新计算前缀和，如果每次查询都有变化，那么复杂度会大幅度增加。有两种数据结构可以高效的处理这个问题：树状数组与线段树。
复制链接

扫一扫