区间DP问题归纳总结

常见问题：

1. 常用技巧：将环形区间转变为线形区间，从而解决环形区间的问题

2. 区间dp记录方案数

3. 区间dp和高精度的结合（将高精度模板结合到dp中去）

代码的实现方式有两种：

1. 迭代式：

   自底向上递推计算，适用于简单的dp过程，一般来说，状态用了几维，就需要写几层for循环，当dp维度较高时显然不适用。

2. 记忆化搜索式：

   自顶向下递归计算，并且在递归时记录已经算过的值，避免重复计算，适用于高维dp或者状态转移较复杂的情况，但缺点有可能出现栈溢出的情况。

---

一般区间dp的状态f[i][j]都表示从第i个元素到第j个元素的一个区间

举例应用：

题目1：石子合并（线形区间dp）

设有N堆石子排成一排，其编号为1, 2, 3, 4 …… , N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这N堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有4堆石子分别为 1 3 5 2， 我们可以先合并 1、2堆，代价为 4，得到 4 5 2， 又合并 1、2堆，代价为 9，得到 9 2 ，再合并得到 11，总代价为 4+9+11=24；

如果第二步是先合并2、3堆，则代价为 7，得到 4 7，最后一次合并代价为 11，总代价为 4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式

第一行一个数N表示石子的堆数 N。

第二行N个数，表示每堆石子的质量(均不超过 1000)。

输出格式

输出一个整数，表示最小代价。

数据范围

1 <= N <= 300

---

分析：

dp

• 状态表示：f[i][j]

  • 集合：f[i][j]表示所有将第i堆石子到第j堆石子合并成一堆的方案的集合

  • 属性：所有合并方式中的最小代价min

• 状态计算：

  划分依据：以最后一次合并时两堆石子的分界线的位置进行划分集合

  f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[i ~ j]);

  其中s[i ~ j]表示第i ~ j堆石子的质量总和，可以用前缀和来计算：s[j] - s[i - 1]

  最终答案即为f[1][n]

代码：

一共有n^2个状态，计算每个状态所需时间为n

时间复杂度为：O(n^3)

#include <iostream>
#include <cstring>
​
using namespace std;
​
const int N = 310;
​
int n;
int a[N]; // 记录每堆石子的质量
int s[N]; // 记录石子质量的前缀和
​
int f[N][N]; // dp
​
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
    
    // 初始化f数组
    memset(f, 0x3f, sizeof f);
    for (int i = 1; i <= n; i ++ ) f[i][i] = 0;
    
    // dp
    // 要保证按照这样的顺序算时，每个状态所依赖的状态都已经算好了
    // 所以要按照区间的长度从小到大来枚举所有的区间，确保区间都是从小到大枚举的
    for (int len = 2; len <= n; len ++ ) // 枚举区间长度
        for (int i = 1; i + len - 1 <= n; i ++ ) // 枚举区间起点
        {
            // 根据区间长度和区间起点的坐标，可以计算出区间终点的坐标
            int j = i + len - 1; // 区间终点
            for (int k = i; k < j; k ++ )
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
                // 合并到左子堆的代价 + 合并到右子堆的代价 + 合并左右子堆的代价
        }
    
    printf("%d\n", f[1][n]);
    
    return 0;
}

本题的石子合并是对给定序列进行合并，是线形的。在本题的基础上，可以扩展出环形石子合并：

题目二：环形石子合并（环形区间dp）

将n堆石子绕圆形操场排放，现要将石子有序地合并成一堆。

规定每次只能选相邻的两堆合并成新的一堆，并将新的一堆的石子数记做该次合并的得分。

请编写一个程序，读入堆数n及每堆的石子数，并进行如下计算：

• 选择一种合并石子的方案，使得做 n - 1次合并得分总和最大。

• 选择一种合并石子的方案，使得做n - 1次合并得分总和最小。

输入格式

第一行包含整数n，表示共有n堆石子。

第二行包含n个整数，分别表示每堆石子的数量。

输出格式

输出共两行：

第一行为合并得分总和最小值，

第二行为合并得分总和最大值。

数据范围

1 <= n <= 200

---

分析：

环形石子合并的方法一般是将环拆开成一条链，然后在此基础上做线形的区间dp

如何把环变成链？

对于环形摆放的石子，每合并相邻的两堆石子就相当于在它们之间连一条线，n堆石子的合并只需要连n - 1条线

那么在n堆相邻石子间连n - 1条线，必定存在相邻的两堆石子之间没有线连接，也就是所谓的缺口，我们可以枚举缺口的位置而将环环形石子的合并变线形石子的合并，本质上就是求n条不同的链上的石子合并问题

由于一共有n个缺口可以枚举，计算每个缺口所产生的线形石子合并问题需要O(n3)的时间复杂度，所以计算本题的时间复杂度为O(n4)。显然会超时

但如果我们将环形上的节点依次排列两遍，形成一条长度为2n的链，如：

1， 2， 3， 1， 2， 3

那么我们可以发现，在环形节点1， 2， 3中，无论枚举哪个缺口，它们所产生的链都在这条长为2n的链上

1， 2， 3， 1， 2， 3

1， 2， 3

------2， 3， 1

------------3， 1， 2

所以我们可以对这条长为2n的链做线形石子合并，得到这条链上的每个区间合并的最小代价，然后再枚举这条长为2n的链上的每一个长为n的区间就可以把上面要求的n条不同的链的最小合并代价都求出来了，最后我们再看哪种拆开方式的合并代价最小，就可以得到答案了，时间复杂度为：O((2n)^3) -> O(n^3)，不会超时

dp思路和上一题一样，在此不再赘述。

代码：

#include <iostream>
#include <cstring>
​
using namespace std;
​
const int N = 410, INF = 0x3f3f3f3f;
​
int n;
int s[N]; // 开始时存放每堆石子数量，之后存放狮子数量的前缀和
​
int f[N][N]; // 求得分最大值
int g[N][N]; // 求得分最小值
​
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);
    for (int i = n + 1; i <= n + n; i ++ ) s[i] = s[i - n];
    
    // 求前缀和
    for (int i = 1; i <= 2 * n; i ++ ) s[i] += s[i - 1];
    
    // f数组求最大值，开始时f数组中的元素默认为0，无需初始化
    
    // g数组求最小值，需要初始化
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= 2 * n; i ++ ) g[i][i] = 0;
    
    for (int len = 2; len <= 2 * n; len ++ )
        for (int i = 1; i + len - 1 <= 2 * n; i ++ )
        {
            int j = i + len - 1;
            for (int k = i; k < j; k ++ )
            {
                f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
                g[i][j] = min(g[i][j], g[i][k] + g[k + 1][j] + s[j] - s[i - 1]);
            }
        }
    
    // 遍历所有的长度为n的区间，求最终答案
    int maxn = -INF, minn = INF;
    for (int i = 1; i <= n; i ++ ) // 枚举区间起点
    {
        maxn = max(maxn, f[i][i + n - 1]);
        minn = min(minn, g[i][i + n - 1]);
    }
    
    printf("%d\n%d\n", minn, maxn);
    
    return 0;
}

题目三：凸多边形的划分（区间dp + 高精度）

本题是区间dp和高精度的结合

给定一个具有N个顶点的凸多边形，将顶点从1至N标号，每个顶点的权值都是一个正整数。

将这个凸多边形划分成N - 2个互不相交的三角形，对于每个三角形，其三个顶点的权值相乘都可得到一个权值乘积，试求所有三角形的顶点权值乘积之和至少为多少。

输入格式

第一行包含整数N，表示顶点数量。

第二行包含N个整数，依次为顶点1至顶点N的权值。

输出格式

输出仅一行，为所有三角形的顶点权值乘积之和的最小值。

数据范围

N <= 50 数据保证所有顶点的权值都小于1e9

---

分析：

可以选取多边形的每一条边作为三角形的底边来划分多边形，然后枚举其他不同的点作为三角形的顶点。由于要求三角形互不相交，所以可以以此三角形将多边形划分为两个不同的多边形，再在此基础上对划分出的不同的多边形做以上同样的操作，就可以得出以这条边作为三角形的底边的权值之和了。

因为对于每一种划分方式，1和n之间的边最终必然属于某个小三角形，一定会被f[1][n]包含，所以只需要枚举其中的一种情况，也就是只计算以其中某一条边作为初始底边的情况就可以计算出f[1][n]了，因此这道题本质上不属于环形问题，是线形的。

dp

• 状态表示：f[L, R]

  • 集合：所有将(L, L + 1), (L + 1, L + 2), ……, (R - 1, R), (R, L)这个多边形划分成三角形的方案

  • 属性：所有三角形顶点权值乘积之和的最小值min

• 状态计算：

  在以(L, R)为初始底边的情况中：

  f[L][R] = min(f[L][R], f[L][K] + f[K][R] + w[L] * w[K] * w[R])

本题中每个三角形的权值最大为1e27，而最多可能有48个三角形出现，因此估算数据的最大位数为30位，需要使用高精度

对于需要使用高精度的题目的做法：

先不写高精度的代码，把样例做对，然后再把其中需要用到高精度的部分换成高精度的代码

这样写代码时可以有效避免错误的发生

对于高精度的计算，我们可以用vector存储数据，定义：vector<int> f[N][N]。但用vector的效率较低，我们在动态规划中使用高精度代码时，可以不用vector存储数据，而将f数组多定义一维f[N][N][M]，用新一维数组的每一位存储实际数据的每一位。

例如：对于f[1][2] = 123，我们可以定义f[N][N][3]，使得f[1][2][0] = 1, f[1][2][1] = 2, f[1][2][2] = 3，也就相当于将f数组的数据类型定义为了一个数组，数组的每一位存储数据的每一位。

这样我们在此基础上使用高精度代码，就可以进行高精度计算了。

代码：

一共有n^2个状态，计算每个状态所需时间为n

时间复杂度为：O(n^3)

#include <iostream>
#include <cstring>
​
using namespace std;
​
const int N = 55, M = 35, INF = 0x3f3f3f3f;
​
typedef long long LL;
​
int n;
int w[N]; // 记录每个顶点的权值
​
LL f[N][N][M]; // dp, 第三维M的每一位记录f[i][j]中保存的数的每一位
​
void add(LL a[], LL b[])
{
    static LL c[M]; // 用static将c数组开在全局区而不是栈区，全局区空间较大
    // 相当于开了一个全局变量，每次使用时不会重新分配空间，效率高了一点点
    memset(c, 0, sizeof c);
    
    LL t = 0;
    for (int i = 0; i < M; i ++ )
    {
        t += a[i] + b[i];
        c[i] = t % 10;
        t /= 10;
    }
    // 由于M大于数组a的位数，所以结束时t == 0，不需要考虑进位
    
    memcpy(a, c, sizeof c);
}
​
void mul(LL a[], LL b) // 高精度乘低精度
{
    static LL c[M];
    memset(c, 0, sizeof c);
    
    LL t = 0;
    for (int i = 0; i < M; i ++ )
    {
        t += a[i] * b;
        c[i] = t % 10;
        t /= 10;
    }
    // 由于M大于数组a的位数，所以结束时t == 0，不需要考虑进位
    
    memcpy(a, c, sizeof c);
}
​
int cmp(LL a[], LL b[])
{
    for (int i = M - 1; i >= 0; i -- )
        if (a[i] > b[i]) return 1;
        else if (a[i] < b[i]) return -1;
    return 0;
}
​
void print(LL a[])
{
    int k = M - 1;
    while (k > 0 && a[k] == 0) -- k;
    for (int i = k; i >= 0; i -- )
        printf("%ld", a[i]);
    puts("");
}
​
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    
    LL temp[M]; // 临时数组，计算新增状态的权值
    for (int len = 3; len <= n; len ++ )
        for (int i = 1; i + len - 1 <= n; i ++ )
        {
            int j = i + len - 1;
            f[i][j][M - 1] = 1; // f[i][j] = INF;
            for (int k = i + 1; k < j; k ++ )
            {
                // 每次计算之前要初始化temp数组元素值为0
                memset(temp, 0, sizeof temp);
                
                // 这里直接将temp[0]初始化为w[i]，并且有乘法操作，所以temp要用LL定义
                temp[0] = w[i]; 
                
                mul(temp, w[k]);
                mul(temp, w[j]);
                add(temp, f[i][k]);
                add(temp, f[k][j]);
                if (cmp(f[i][j], temp) > 0) // temp < f[i][j]
                    memcpy(f[i][j], temp, sizeof temp);
            }
        }
    
    print(f[1][n]);
    
    return 0;
}

题目四：加分二叉树 （区间dp求方案数）

区间dp记录方案数

设一个n个节点的二叉树 tree 的中序遍历为（1,2,3,…,n)，其中数字 1,2,3,…,n为节点编号。

每个节点都有一个分数（均为正整数），记第i个节点的分数为 di，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：     

subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数 

若某个子树为空，规定其加分为1。

叶子的加分就是叶节点本身的分数，不考虑它的空子树。

试求一棵符合中序遍历为（1,2,3,…,n）且加分最高的二叉树 tree。

要求输出： 

（1）tree的最高加分 

（2）tree的前序遍历

输入格式

第1行：一个整数n，为节点个数。 

第2行：n个用空格隔开的整数，为每个节点的分数（0<分数<100）。

输出格式

第 1行：一个整数，为最高加分（结果不会超过int范围）。     

第2行：n个用空格隔开的整数，为该树的前序遍历。如果存在多种方案，则输出字典序最小的方案。

数据范围

n < 30

---

分析：

dp

• 状态表示：f[L, R]

  • 集合：所有中序遍历是[L, R]这一段的二叉树的集合

  • 属性：所有这些二叉树的分值的最大值max

• 状态计算：

  划分依据：找到最后一个不同点，依据这些不同点来划分子集

  不同点：中序遍历中根节点的位置

  根节点位置为k时的二叉树的分值：w[k] + f[L, k - 1] * f[k + 1, R]

求方案数的过程就是记录每次决策的过程

用g[L, R]存储当二叉树的分值取得最大值时，这个区间的根节点的编号

要输出前序遍历（根左右）的字典序最小的序列，那么根节点的编号要尽可能小，故在dp时要从小到大枚举根节点的值以保证答案的根节点最小，在比较得出二叉树最大分值时，判断语句if (score > f[l][r])，不能等于。

如果判断语句if (score > f[l][r])或者从大到小枚举根节点的值，得到的序列都为字典序最大的序列

代码：

一共有n^2个状态，计算每个状态所需时间为n

时间复杂度为：O(n^3)

#include <iostream>
#include <cstring>
​
using namespace std;
​
const int N = 30;
​
int n;
int w[N]; // 记录每个节点的分数
​
int f[N][N]; // dp
int g[N][N]; // 记录当分数取得最大值时，每个区间的根节点的编号
​
void dfs(int l, int r)
{
    if (l > r) return;
    printf("%d ", g[l][r]); // 遍历根节点
    
    int root = g[l][r];
    dfs(l, root - 1); // 遍历左子树
    dfs(root + 1, r); // 遍历右子树
}
​
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    
    for (int len = 1; len <= n; len ++ )
        for (int l = 1; l + len - 1 <= n; l ++ )
        {
            int r = l + len - 1;
            if (len == 1) // 说明此节点是叶节点
            {
                f[l][r] = w[l]; // 没有左右子树
                g[l][r] = l; // 根节点就是它本身
            }
            else
            {
                for (int k = l; k <= r; k ++ ) // 存在左右子树为空的情况，故k从l遍历到r
                {
                    // 当k == l时，k - 1 < l，必须特判left = 1，
                    int left = k == l ? 1 : f[l][k - 1];
                    // 当k == r时，k + 1 > r，必须特判right = 1
                    int right = k == r ? 1 : f[k + 1][r];
                    
                    int score = left * right + w[k];
                    if (score > f[l][r]) // score必须 > f[l][r]，不能等于
                    {
                        f[l][r] = score;
                        g[l][r] = k; // 记录区间[l, r]的根节点的编号
                    }
                }
            }
        }
    
    printf("%d\n", f[1][n]);
    
    dfs(1, n);
    
    return 0;
}

题目五：棋盘分割（二维区间dp）

二维区间dp问题

将一个8×8的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n−1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

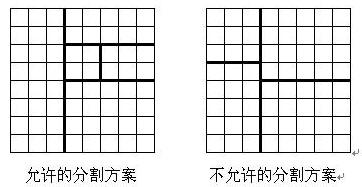
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。

现在需要把棋盘按上述规则分割成 nn 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差

，其中平均值

，xixi 为第 ii 块矩形棋盘的总分。

请编程对给出的棋盘及n，求出均方差的最小值。

输入格式

第1行为一个整数 n。

第2行至第9行每行为8个小于 100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式

输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围

1 < n < 15

---

分析：

如果题目中要进行复杂表达式的比较，可以先对表达式进行化简，然后对化简后的表达式进行求值比较，可以简化比较过程的代码。

dp

• 状态表示：f[x1][y1][x2][y2][k]

  • 集合：将子矩阵(x1, y2)(x2, y2)切分成k部分的所有方案

  • 属性：

    

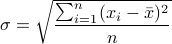
    的最小值

• 状态计算：

  划分集合：可以根据每次切分棋盘时是横切还是纵切对切分方式进行划分，由于题中要不断切割棋盘剩下的部分，那么我们可以在每次切分后对保留两块棋盘中的哪一部分再次进行划分，对保留的棋盘继续切分。

  横切和纵切一共有14种切法，每种切法有两种保留方法，故对于每个集合可以划分成28个子集

由于本题的集合状态有5维，所以用记忆化搜索的方式计算：

由于本题涉及到double类型的计算，要注意：

对于double类型的数组：

memset(f, 127, sizeof f); // 将数组中的double类型元素全部初始化为正无穷 memset(f, 0, sizeof f); // 将数组中的double类型元素全部初始化为0 memset(f, 128, sizeof f); // 将数组中的double类型元素全部初始化为负无穷

代码：

#include <iostream>
#include <cstring>
#include <cmath>
​
using namespace std;
​
const int N = 15, M = 9;
​
const double INF = 1e9;
​
int n, m = 8;
double s[M][M]; // 由于参与的都是浮点型的运算，所以将前缀和数组定义为double类型
double f[M][M][M][M][N];
​
// 棋盘分值平均值
double ave;
​
// 计算 (xi - ave)^2 / n
double get(int x1, int y1, int x2, int y2)
{
    double sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] - ave;
    return sum * sum / n;
}
​
// 求得的结果是均方差的平方值，最后需要开方
// 自顶向下记忆化搜索
double dp(int x1, int y1, int x2, int y2, int n)
{
    // 数组表示太长，用引用替代
    double& v = f[x1][y1][x2][y2][n]; 
    if (v >= 0) return v; // 说明已经被计算过了
    
    // n为分割成的块数，当n == 1时无需再分割，在返回分值的同时记得给v赋值
    if (n == 1) return v = get(x1, y1, x2, y2);
    
    v = INF; // 由于要求最小方差，所以要初始化为INF
    // 横切
    for (int i = 1; i < 8; i ++ )
    {
        // 保留上半部分
        v = min(v, dp(x1, y1, i, y2, n - 1) + get(i + 1, y1, x2, y2));
        // 保留下半部分
        v = min(v, dp(i + 1, y1, x2, y2, n - 1) + get(x1, y1, i, y2));
    }
    // 纵切
    for (int i = 1; i < 8; i ++ )
    {
        // 保留左半部分
        v = min(v, dp(x1, y1, x2, i, n - 1) + get(x1, i + 1, x2, y2));
        // 保留右半部分
        v = min(v, dp(x1, i + 1, x2, y2, n - 1) + get(x1, y1, x2, i));
    }
    
    return v;
}
​
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= m; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            scanf("%lf", &s[i][j]);
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    
    // s数组为double类型，不需要强制类型转换
    ave = s[m][m] / n;
    
    // double数组全部初始化成-INF
    // 作用是判断f数组中的值是否已经被计算过
    memset(f, 128, sizeof f);
    // memset(f, 127, sizeof f); 初始化为INF
    
    // 记忆化搜索dp
    double res = dp(1, 1, 8, 8, n);
    
    // 记得开平方和保留三位小数
    printf("%.3lf\n", sqrt(res));
    
    return 0;
}