多目标问题
即非单目标问题,目标函数由多个(2+)子目标函数组成,一个X对应多个Y。
例如X(2,3)->Y=(3,2,4),X(44,7)->Y=(1,5,1),X(9,9)->Y=(6,2,9).即点x(2,3)对应的y值为(3,2,4),有3个目标需要优化。如下图目标空间有f1,f2两个目标需要优化,是个两目标优化问题:

多峰问题
即存在多个局部最优点。如下图所示(越大越好,Z轴为目标函数值):

又比如下图(越小越好):
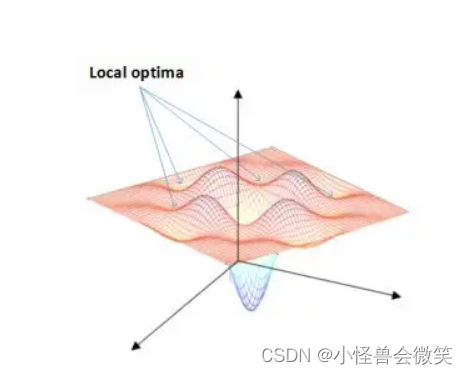
该问题的挑战是:容易陷入局部最优,难以发现全局最优。
多模态问题
即多个X对应一个目标函数Y的值。
例如:X(2,3)->Y=0.45,X(44,7)->Y=0.45,X(9,9)->Y=0.45.即点(2,3)、(44,7)和(9,9)对应的y值均为0.45.
给出了一个多模态双目标优化问题,该问题有两个全局最优解集。
其中左边决策空间即X,右边Y是f1和f2共同构成的两目标pareto front。

该问题的挑战是:决策空间的多个区域的点可能会相互干扰,造成收敛困难。以及最终可能多样性不强,如上图可能最后的解集只有PS1中解。
动态问题
即问题的目标函数随时间会发生变化,pareto解会随时间而改变。如下图,从左到右,PS从p1一直变化到p8。

该问题的挑战是:需要实时评估、学习Pareto front。
噪声环境问题
即目标函数计算时存在噪音,多次评估的结果可能不同(但一般偏离不大)。
该问题的挑战是:噪声会影响性能。
超多目标问题
即多目标问题中目标数m>>3(远远大于3)。
该问题的挑战是:通常我们是重组目标函数,使得目标数目下降到一定的个数,例如原问题有300个目标,重组后降到10个进行优化。所以挑战是重组的效率不高。








 本文探讨了多目标优化问题,包括其特点如多峰、多模态、动态和噪声环境问题,以及超多目标问题。这些挑战在于寻找全局最优、避免局部最优、处理目标函数变化和噪声干扰等。解决策略涉及动态适应、目标重组及优化算法的应用。
本文探讨了多目标优化问题,包括其特点如多峰、多模态、动态和噪声环境问题,以及超多目标问题。这些挑战在于寻找全局最优、避免局部最优、处理目标函数变化和噪声干扰等。解决策略涉及动态适应、目标重组及优化算法的应用。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










