渐进分析-时间复杂度

众所周知，数据结构是一种有效组织数据的方式，效率是用时间或空间来衡量的。因此，理想的数据结构是一种占用尽可能少的时间来执行其所有操作和内存空间的结构。我们的重点是找到时间复杂度而不是空间复杂度，通过找到时间复杂度，我们可以决定哪种数据结构最适合算法。

本文主要参考 数据结构可视化动画版-图码

我们脑海中出现的主要问题是，我们应该在什么基础上比较数据结构的时间复杂度？可以根据对它们执行的操作来比较时间复杂度。让我们考虑一个简单的例子。

假设我们有一个包含 100 个元素的数组，并且我们想要在数组的开头插入一个新元素。这成为一项非常繁琐的任务，因为我们首先需要将元素向右移动，然后在数组的开头添加新元素。

假设我们将链表视为一种数据结构，在开头添加元素。链表包含两部分，即数据和下一个节点的地址。我们只需将第一个节点的地址添加到新节点中，头指针现在将指向新添加的节点。因此，我们得出结论，在链表的开头添加数据比在数组中添加数据要快。通过这种方式，我们可以比较数据结构并选择最佳的数据结构来执行操作。

如何找到执行操作的时间复杂度或运行时间？

实际运行时间的测量根本不切实际。执行任何操作的运行时间取决于输入的大小。我们通过一个简单的例子来理解这个说法。

假设我们有一个包含五个元素的数组，并且我们想在数组的开头添加一个新元素。为了实现这一点，我们需要将每个元素向右移动，并假设每个元素需要一个时间单位。有五个元素，因此需要五个时间单位。假设数组中有 1000 个元素，那么移位需要 1000 个单位的时间。结论是时间复杂度取决于输入大小。

因此，如果输入大小为 n，则 f(n) 是表示时间复杂度的 n 的函数。

如何计算f(n)？

对于较小的程序，计算 f(n) 的值很容易，但对于较大的程序，就没那么容易了。我们可以通过比较它们的 f(n) 值来比较数据结构。我们可以通过比较它们的 f(n) 值来比较数据结构。我们将找到 f(n) 的增长率，因为可能存在较小输入大小的一种数据结构优于另一种数据结构，但对于较大输入大小则不然。现在，如何求 f(n)。

让我们看一个简单的例子。

f(n) = 5n 2 + 6n + 12

其中 n 是执行的指令数，它取决于输入的大小。

当n=1时

所占的运行时间百分比= * 100 = 21.74%

6n 所占的运行时间百分比 = * 100 = 26.09%

运行时间百分比 12 = * 100 = 52.17%

从上面的计算可以看出，大部分时间都被12占用了。但是，我们必须找到f(n)的增长率，我们不能说最大时间被12占用。让我们假设n的不同值来找到f(n)的增长率。

n		6n	12
1	21.74%	26.09%	52.17%
10	87.41%	10.49%	2.09%
100	98.79%	1.19%	0.02%
1000	99.88%	0.12%	0.0002%

从上表中我们可以看出，随着n值的增加，的运行时间增加，而6n和12的运行时间也减少。因此，可以观察到，对于较大的 n 值，平方项消耗了几乎 99% 的时间。由于 项贡献最多，因此我们可以消除其余两项。

所以，

f(n) =

在这里，我们得到了近似时间复杂度，其结果非常接近实际结果。这种时间复杂度的近似度量称为渐近复杂度。在这里，我们不计算确切的运行时间，我们正在消除不必要的项，我们只是考虑占用最多时间的项。

在数学分析中，算法的渐近分析是一种定义其运行时性能的数学边界的方法。使用渐近分析，我们可以轻松得出算法的平均情况、最佳情况和最坏情况。

它用于以数学方式计算算法内任何操作的运行时间。

示例：一个操作的运行时间为 x(n)，另一操作的运行时间计算为 f(n2)。它是指对于第一个操作，运行时间将随着“n”的增加而线性增加，而对于第二个操作，运行时间将呈指数增加。类似地，如果 n 非常小，则两个操作的运行时间将相同。

通常，算法所需的时间分为三种类型：

最坏的情况：它定义了算法需要花费大量时间的输入。

平均情况：程序执行所需的平均时间。

最佳情况：它定义了算法花费最短时间的输入

渐近符号

用于计算算法运行时间复杂度的常用渐近符号如下：

• 大 oh 符号 (?)
• 欧米茄表示法 (Ω)
• Theta 表示法 (θ)

大 oh 表示法 (O)

• Big O 表示法是一种渐近表示法，它通过简单地提供函数的增长阶数来衡量算法的性能。
• 该表示法提供了函数的上限，确保函数的增长速度永远不会超过上限。因此，它给出了函数的最小上限，以便函数的增长速度永远不会超过该上限。

它是表达算法运行时间上限的正式方式。它测量时间复杂度的最坏情况或算法完成其操作的最长时间。其表示如下图所示：

例如：

如果f(n)和g(n)是为正整数定义的两个函数，

那么f(n) = O(g(n))因为f(n) 是 g(n) 的大 oh或 f(n) 的量级为 g(n)) 如果存在常量 c 并且不存在这样的常数：

f(n)≤cg(n) 对于所有 n≥no

这意味着 f(n) 的增长速度不会快于 g(n)，或者 g(n) 是函数 f(n) 的上限。在这种情况下，我们计算的是函数的增长率，最终计算出函数的最差时间复杂度，即算法可以执行的最差程度。

我们通过例子来理解

示例 1：f(n)=2n+3 、g(n)=n

现在，我们必须找到f(n)=O(g(n)) 吗？

要检查 f(n)=O(g(n))，它必须满足给定条件：

f(n)<=cg(n)

首先，我们将 f(n) 替换为 2n+3，g(n) 替换为 n。

2n+3 <= cn

假设 c=5, n=1 那么

2*1+3<=5*1

5<=5

当n=1时，上述条件成立。

如果n=2

2*2+3<=5*2

7<=10

对于n=2，上述条件成立。

我们知道，对于n的任何值，都会满足上述条件，即2n+3<=cn 如果c的值等于5，那么就会满足条件2n+3<=cn 我们可以从1开始取n的任何值，它总是满足。因此，我们可以说，对于某些常数 c 和某些常数 n0，总是满足 2n+3<=cn 由于满足上述条件，所以 f(n) 是 g(n) 的大 oh 或者我们可以说 f(n) 线性增长。因此，得出cg(n)是f(n)的上限的结论。它可以图形化地表示为：

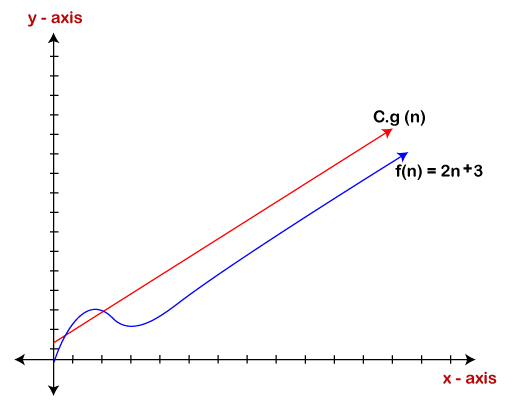
使用大符号的想法是给出特定函数的上限，最终导致给出最坏时间复杂度。它保证了特定函数不会突然表现为二次或三次形式，它只是在最坏情况下以线性方式表现。

欧米茄表示法 (Ω)

• 它基本上描述了与大符号相反的最佳情况。
• 它是表示算法运行时间下限的正式方法。它衡量算法完成所需的最佳时间或最佳情况的时间复杂度。
• 它决定了算法可以运行的最快时间。

如果我们要求算法至少花费一定的时间而不使用上限，我们使用大Ω表示法，即希腊字母“omega”。它用于限制大输入大小的运行时间的增长。

如果f(n)和g(n)是为正整数定义的两个函数，

那么f(n) = Ω (g(n))因为f(n) 是 g(n) 的 Omega或 f(n) 的量级为 g(n)) 如果存在常数 c 并且不存在这样的常数：

f(n)>=cg(n) 对于所有 n≥no 且 c>0

让我们考虑一个简单的例子。

如果 f(n) = 2n+3, g(n) = n，

f(n)= Ω (g(n)) 吗？

它必须满足条件：

f(n)>=cg(n)

为了检查上述条件，我们首先将 f(n) 替换为 2n+3，将 g(n) 替换为 n。

2n+3>=c*n

假设c=1

2n+3>=n（对于从 1 开始的任何 n 值，该方程都成立）。

由此证明g(n)是2n+3函数的大omega。

从上图中我们可以看出，当 c 的值等于 1 时，g(n) 函数是 f(n) 函数的下界。因此，这种表示法给出了最快的运行时间。但是，我们对找到最快的运行时间更感兴趣，我们感兴趣的是计算最坏的情况，因为我们想检查我们的算法是否有更大的输入，即最坏的时间是多少，以便我们可以在进一步的过程中做出进一步的决定。

Theta 表示法 (θ)

• theta 表示法主要描述平均情况场景。
• 它代表算法的实际时间复杂度。每次，算法都不会表现最差或最好，在现实世界的问题中，算法主要在最坏情况和最好情况之间波动，这给了我们算法的平均情况。
• 大theta主要用于最坏情况和最好情况的值相同的情况。
• 它是表达算法运行时间的上限和下限的正式方式。

让我们从数学上理解大θ符号：

令 f(n) 和 g(n) 为 n 的函数，其中 n 是执行程序所需的步骤：

f(n)=θg(n)

仅当当

c1.g(n)<=f(n)<=c2.g(n)

其中函数有两个极限，即上限和下限，f(n) 介于两者之间。当且仅当c1.g(n)小于或等于 f(n) 并且 c2.g(n) 大于或等于 f(n) 时，条件 f(n)= θg(n) 才成立。theta 表示法的图形表示如下：

让我们考虑相同的例子，其中
f(n)=2n+3
g(n)=n

由于 c1.g(n) 应小于 f(n)，因此 c1 必须为 1，而 c2.g(n) 应大于 f(n)，因此 c2 等于 5。 c1.g(n) 是 f(n) 的下限，而 c2.g(n) 是 f(n) 的上限。

c1.g(n)<=f(n)<=c2.g(n)

将 g(n) 替换为 n，将 f(n) 替换为 2n+3

c1.n <=2n+3<=c2.n

如果c1=1，c2=2，n=1

1*1 <=2*1+3 <=2*1

1 <= 5 <= 2 // 对于 n=1，满足条件 c1.g(n)<=f(n)<=c2.g(n)

如果n=2

1*2<=2*2+3<=2*2

2<=7<=4 // 对于 n=2，满足条件 c1.g(n)<=f(n)<=c2.g(n)

因此，我们可以说，对于任何n值，它都满足条件c1.g(n)<=f(n)<=c2.g(n)。由此证明f(n)是g(n)的大θ。因此，这是提供实际时间复杂度的平均情况场景。

为什么我们有三种不同的渐近分析？

我们知道，大 omega 代表最好的情况，大 oh 代表最坏的情况，而大 theta 代表平均情况。现在，我们将找出线性搜索算法的平均情况、最差情况和最佳情况。

假设我们有一个包含 n 个数字的数组，并且我们想要使用线性搜索来查找数组中的特定元素。在线性搜索中，每个元素都会在每次迭代时与搜索到的元素进行比较。假设，如果仅在第一次迭代中找到匹配，那么最好的情况将是 Ω(1)，如果该元素与最后一个元素（即数组的第 n 个元素）匹配，那么最坏的情况将是 O(n)。平均情况是最好情况和最坏情况的中间，因此变成θ(n/1)。在时间复杂度中可以忽略常数项，因此平均情况为 θ(n)。

因此，三种不同的分析提供了实际函数之间的适当界限。这里，边界意味着我们有上限和下限，这确保算法仅在这些限制之间运行，即不会超出这些限制。

常见渐近符号

constant	-	?(1)
linear	-	?(n)
logarithmic	-	?(log n)
n log n	-	?(n log n)
exponential	-	2?(n)
cubic	-	?(n3)
polynomial	-	n?(1)
quadratic	-	?(n2)