在本科的时候就学过数据结构，那时候用的是清华大学C++版本的教材。上研究生之后，在实际学习与工程中愈发发觉数据结构的重要性，所以重新进行了数据结构的再学习，采用了清华大学邓俊辉副教授的视频课程，同时在学习中整理笔记如下。
1、绪论
- （a）计算
两个重要方面： 正确性：算法功能与问题要求一致？数学证明？
成本：运行时间，所需存储空间 如何度量，如何比较？
进行归纳概括：划分等价类 观察：问题实例的规模
特定算法+不同实例
在规模同为n的所有实例中，只关注最坏（成本最高）者
对象：规律、技巧
目标：高效，低耗
- （b）计算模型 定义一个公共的、理想的尺子
算法，在特定计算模型下，旨在解决特定问题的指令序列：输入、输出、正确性、确定性、可行性、有穷性
Hailstone序列（对有穷性的讨论）
// HailStone.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "iostream"
#include "windows.h"
using namespace std;
int hailstone(long n)
{
int length=1;
while (1<n)
{
n=(n%2)?n*3+1:n/2;
length++;
}
return length;
}
int _tmain(int argc, _TCHAR* argv[])
{
long n;
cin>>n;
int length = hailstone(n);
cout<<length ;
system("pause");
return -1;
}
输入：7 输出：17
输入：27 输出：112
有穷性不确定，所以该程序未必是一个算法，程序≠算法
算法：如何设计、优化？
什么是一个好的算法？
正确：能够从正确处理各种输入
健壮：能够辨别不合法的输并做适当处理
可读：结构化+命名准确+注释+……
效率：速度尽可能快，存储空间尽可能少
- （c）大O记号
渐进分析，当n>>2后，对于规模为n的输入，算法T（n），S（n）（通常不关心）
大O记号
常系数可忽略
低次项可忽略
其它记号：大Ω 大Θ
O（1） 常数复杂度
常数、较大的常数、常数的四则计算的常数，甚至常数的常数次幂，都可以记做O（1）
这类算法的效率最高
什么样的代码段符合？
不含转向：循环、调用、递归等，必顺序执行
O（logn） 对数复杂度
常底数无所谓，常数次幂无所谓，对数多项式（低次项可以忽略）
这类算法非常有效，复杂度无限接近于常数
O（n^c） 多项式复杂度
一般的，可以记做最高次的复杂度
@线性复杂度：O（n）类
@从O（n）到O（n^2）
@幂：O（n^c） 这类算法的效率通常认为已经可以令人满意 （可解问题，不是难解问题）
O（2^n） 指数复杂度
T（n）=a^n 这类算法的计算成本增长极快，通常认为不可忍受
从O（n^c）到O（2^n），是从有效算法到无效算法的分水岭
很多问题O（2^n）算法往往是显而易见的，但是写成O（n^c）十分困难，甚至徒劳
美国大选模型：
直觉算法：逐一枚举S的每一自己，并统计其中元素的总和 2^n 指数规模 直觉算法需要迭代2^n轮，并（在最坏的情况下）至少需要花费这么多的时间，不甚理想！
有更好的算法吗？ 没有！！！！ 2-subeet is NP-complete ：
就目前的计算模型而言，不存在可在多项式时间内回答此问题的算法，就此意义而言，上述的直觉算法已属最优
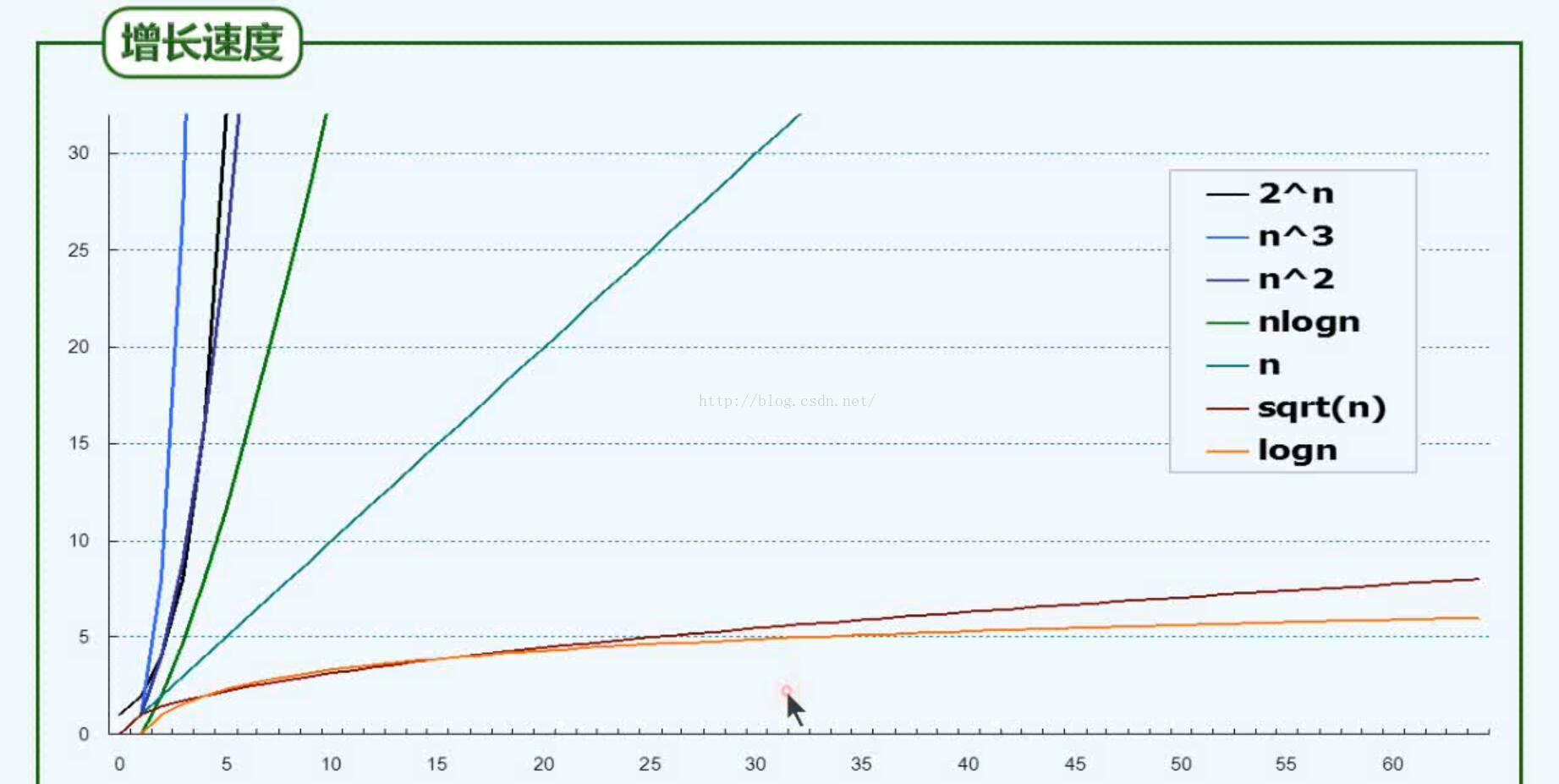
增长速度：
- （d）算法分析 去粗存精的估算
</pre><pre name="code" class="cpp">for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
O1Operation(i,j);
}
}for (int i = 0; i < n; i++)
{
for (int j = 0; j < i;j++)
{
O1Operation(i,j);
}
}for (int i = 0; i < n; i++)
{
for (int j = 0; j < i;j+=2013)
{
O1Operation(i,j);
}
}算术级数
for (int i = 0; i < n; i<<=1)
{
for (int j = 0; j < i; j += 2013)
{
//O1Operation(i,j);
}
}
问题：
对于某些问题，无论输入n多么大，其计算复杂度都是不变的
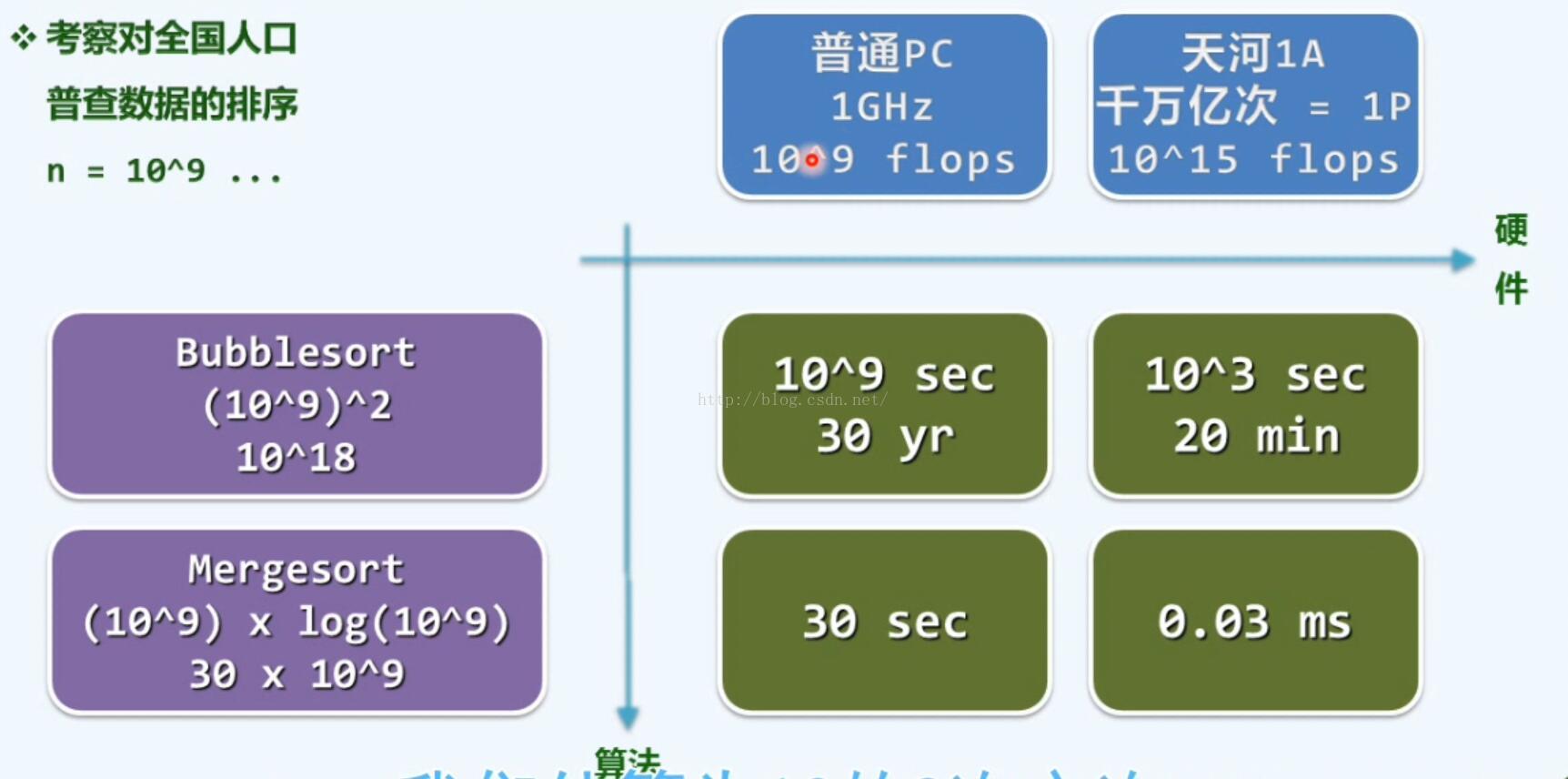
冒泡排序算法：给定n个证书，将他们按非降序排列
扫描交换：反复扫描序列，依次比较每一对相邻元素，如有必要，交换值，若正堂扫描都没有进行交换，则排序完成，否则，再做一趟扫描交换
void bubblesort (int A[],int n) //今后将进行进一步改进
{
for (bool sorted = false ;sorted =!sorted ; n--)//逐趟扫描脚环，直至完全有序
{
for ( int i = 1; i<n;i++) //自左向右，逐对检查数组内各相邻元素
{
if(A[i-1]>A[i]) //若逆序，则
{
swap(A[i-1],A[i]); //令其互换，同时
sorted = false; //清除（全局）有序标志
}
}
}
}对该算法的证明：
问题：该算法必然会结束？至多需迭代多少趟？
不变性，经过K轮扫描交换后，最大的k个元素必然就位
单调性：经过k轮扫描交换后，问题规模缩减至n-k
正确性：经过至多n趟扫描后，算法必然终止，且能给出正确解答
Back-Of-The-Envelop-Calculation 封底分析
直观的概念： 1天 = 24h * 60 min * 60sec ≈ 25*4000 = 10^5 sec
1生≈1世纪 = 100yr *365 = 3*10^9 sec
为祖国健康工作50年 ≈ 1.6 * 10^9 sec
三生三世 10^10 sec
宇宙大爆炸至今 10^21sec
-
- e）迭代与递归 如何设计一个高效的DSA ：凡治众如治寡，分数是也 减而治之/分而治之
问题1：计算任意n个整数之和：实现：逐一取出每个元素，累加之 O（n） 空间复杂度：考量除了输入空间之外用于算法的空间总量 O（2）
减而治之：为求解一个大规模的问题，可以——将其分为两个子问题，其一平凡，另一规模所见 分别求解子问题
数组求和：线性递归
//数组求和，递归算法 int sum(int A[] , int n) { return (n<2)?0:sum(A,n-1)+A[n-1]; }
分而治之：数组求和，二分递归
递归跟踪分析：直观形象，仅适用于简明的递归模式 检查每个递归实例，累计所需时间，（调用语句本身，计入对应的子实例），其总和即算法执行时间
递推方程：简洁抽象，更适用于更加复杂的递归
T（n） = T（n-1） + O（1）
T（0） = O（1）
问题2：任意数组A，将其前后倒置 统一接口：void reverse(int *a , int lo, int hi)
递归版
//数组倒置，递归算法 void reverse(int *A, int lo, int hi) { if(lo < hi) { swap(A[lo],A[hi]); reverse(A,lo +1,hi -1); } }
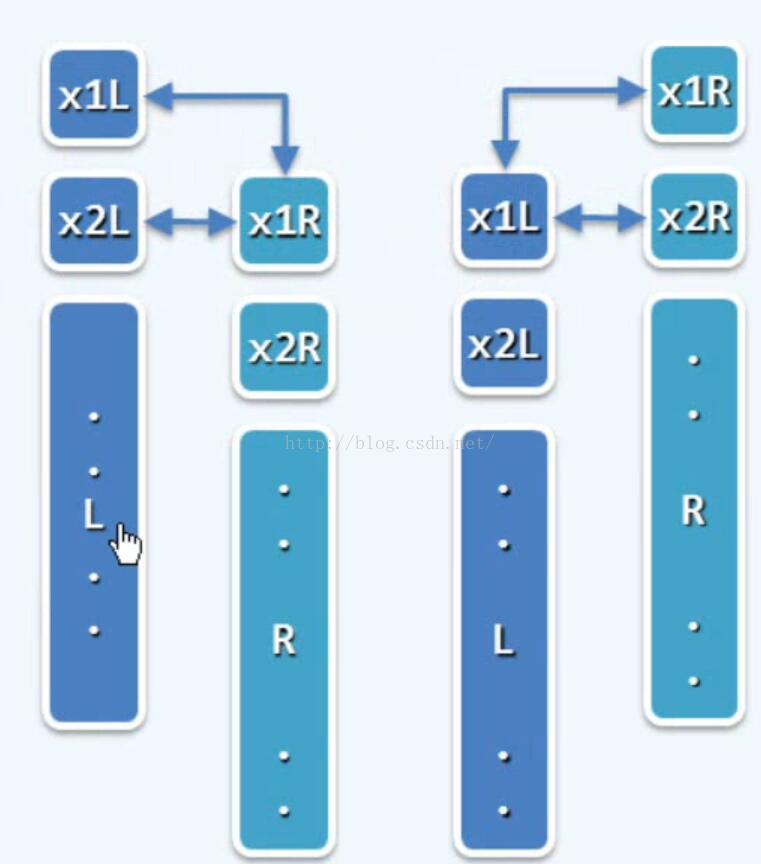
Max2:迭代1：从数组去见A[lo,hi)中找出最大的两个正式A[X1]和A[x2]，元素比较的次数要求尽可能地少
//递归，分而治之 T(n)=2*T(n/2)+2<=5n/3 -2 void max2(int A[] , int lo , int hi, int &x1 , int &x2) { if (lo +2 ==hi){;return;} if (lo +3 == hi){;return;} int mi = (lo+hi)/2; int x1L,x2L; max2(A, lo, mi, x1L, x2L); int x1R,x2R; max2(A, lo, mi, x1R, x2R); if(A[x1L]>A[x1R]) { x1=x1L; x2 = (A[x2L]>A[x1R])?x2L:x1R; } else { x1=x1R; x2 = (A[x1L]>A[x2R])?x1L:x2R; } }
- （f）动态规划 make it work make it right make it fast
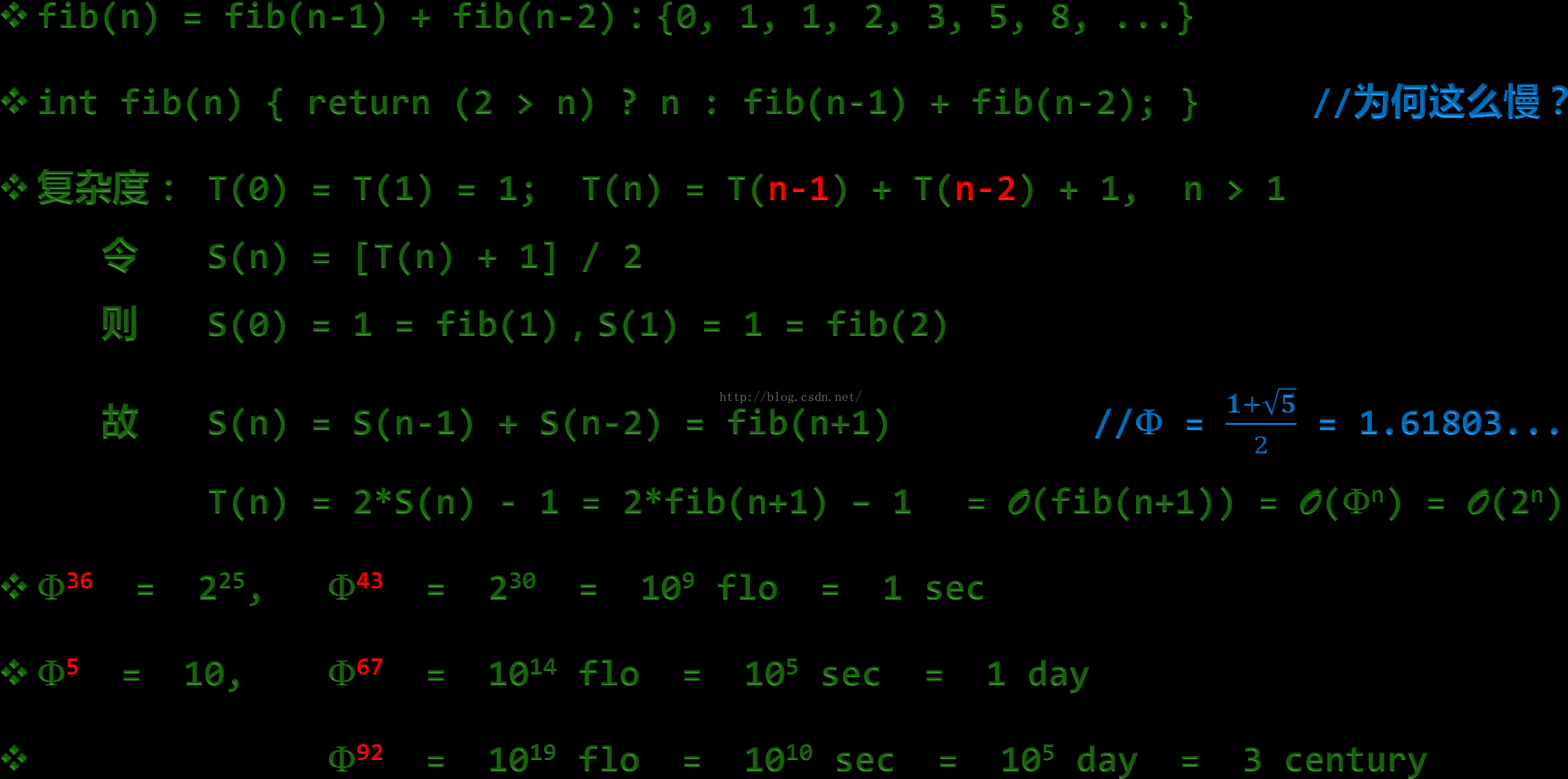
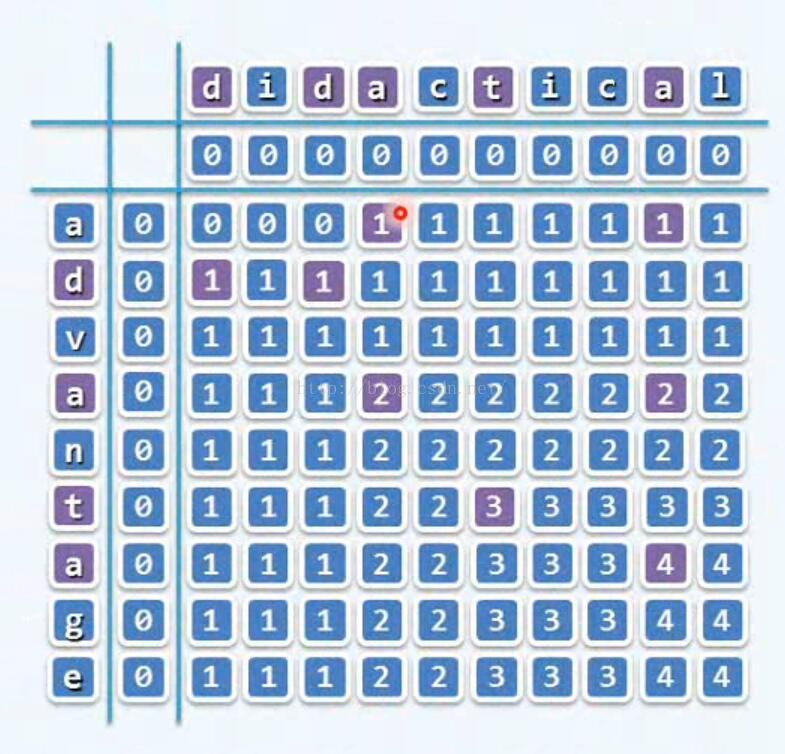
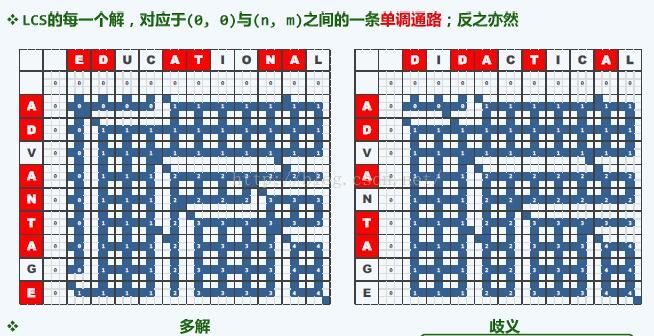算法的效率并不是很高
- （e）迭代与递归 如何设计一个高效的DSA ：凡治众如治寡，分数是也 减而治之/分而治之
数组求和：线性递归
//数组求和，递归算法
int sum(int A[] , int n)
{
return (n<2)?0:sum(A,n-1)+A[n-1];
}分而治之：
数组求和，二分递归
递归跟踪分析：直观形象，仅适用于简明的递归模式 检查每个递归实例，累计所需时间，（调用语句本身，计入对应的子实例），其总和即算法执行时间
递推方程：简洁抽象，更适用于更加复杂的递归
T（n） = T（n-1） + O（1）
T（0） = O（1）
问题2：任意数组A，将其前后倒置 统一接口：void reverse(int *a , int lo, int hi)
递归版
//数组倒置，递归算法
void reverse(int *A, int lo, int hi)
{
if(lo < hi)
{
swap(A[lo],A[hi]);
reverse(A,lo +1,hi -1);
}
}Max2:迭代1：从数组去见A[lo,hi)中找出最大的两个正式A[X1]和A[x2]，元素比较的次数要求尽可能地少
//递归，分而治之 T(n)=2*T(n/2)+2<=5n/3 -2
void max2(int A[] , int lo , int hi, int &x1 , int &x2)
{
if (lo +2 ==hi){;return;}
if (lo +3 == hi){;return;}
int mi = (lo+hi)/2;
int x1L,x2L; max2(A, lo, mi, x1L, x2L);
int x1R,x2R; max2(A, lo, mi, x1R, x2R);
if(A[x1L]>A[x1R])
{
x1=x1L;
x2 = (A[x2L]>A[x1R])?x2L:x1R;
}
else
{
x1=x1R;
x2 = (A[x1L]>A[x2R])?x1L:x2R;
}
}
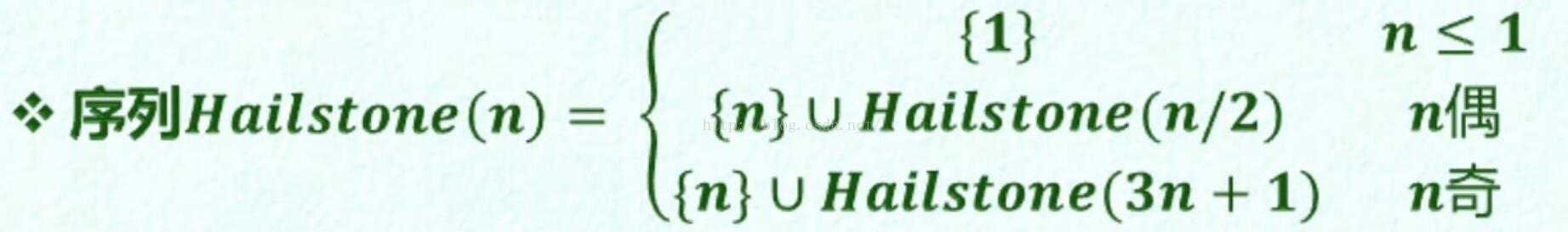
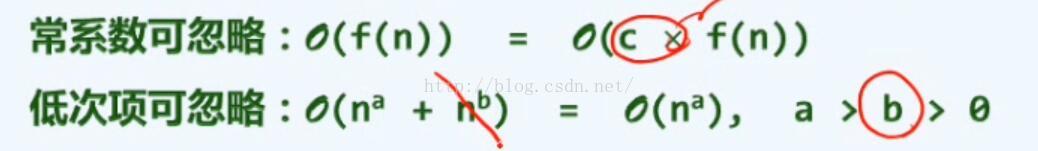
366
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
