华为食堂也开始末位淘汰了，今年真的卷。。。-CSDN博客

本文链接：https://blog.csdn.net/abcdef314159/article/details/136144614

文章讨论了二叉树层序遍历的问题，提及LeetCode第102题的背景，以及在美团面试中的应用场景，介绍了Java、C++、C和Python的实现方法，展示了如何通过BFS遍历解决此问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

(关注数据结构和算法，了解更多新知识)

最近在网上看到一个帖子，一网友发文称：华为食堂也开始末位淘汰了，今年是真的卷。从网友发的图中我们可以看到实际上是两家餐厅竞争，最终确定谁会留下来。

放大后的图片（餐厅就餐率争霸赛）

对于这种竞争我是乐见其成的，有竞争是好事。就像当年的滴滴和快滴竞争，为了打价格战他们不停的发红包，可是自从滴滴和快滴合并之后就形成了垄断，现在在打车也很少有优惠了。

餐厅竞争让更符合大家口味的，更物美价廉的餐厅留下来也是一件好事，我们来看一下大家对这件事是怎么评论的，有一位认证为华为员工的网友说：园区的鸭子天鹅下蛋也要按绩效排序。

--------------下面是今天的算法题--------------

今天这题是LeetCode的第102题：二叉树的层序遍历，一网友在美团（应该不是送外卖的）的面试中遇到过这道题，我们来看下。

问题描述

来源：LeetCode第102题

难度：中等

给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

示例 1：

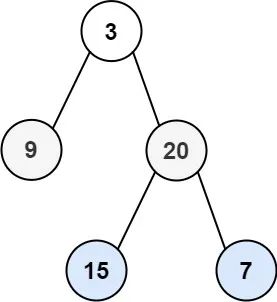
示例1：

输入：root = [3,9,20,null,null,15,7]

输出：[[3],[9,20],[15,7]]

示例2：

输入：root = [1]

输出：[[1]]

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

问题分析

这题是让返回二叉树节点的层序遍历，实际上就是对二叉树进行BFS遍历，关于二叉树的BFS遍历以及使用模板，我们在《算法秘籍》中都有详细的介绍，具体大家可以去看下。

二叉树的BFS遍历一般是配合着队列来使用的，每次遍历队列之前需要先计算队列中元素的个数，这个个数就是当前层节点的个数。因为我们在遍历二叉树的时候当前层和下一层的部分节点有可能会同时存在于队列中，为了防止把下一层的节点添加到当前层中，所以需要先记录。

JAVA：

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> ans = new LinkedList<>();
    if (root == null)
        return ans;
    Queue<TreeNode> queue = new LinkedList<>();// 创建队列
    queue.offer(root);// 把根节点添加到队列中
    while (!queue.isEmpty()) {
        int levelCount = queue.size();// 每层的节点个数
        // 每层的集合。
        List<Integer> subList = new ArrayList<>();
        // 遍历当前层的所有节点，顺便把下一层的所有节点添加到队列中。
        for (int i = 0; i < levelCount; i++) {
            TreeNode cur = queue.poll();// 节点出队
            subList.add(cur.val);
            // 左右子节点如果不为空就添加到队列中。
            if (cur.left != null)
                queue.offer(cur.left);
            if (cur.right != null)
                queue.offer(cur.right);
        }
        ans.add(subList);// 当前层的集合添加到队列中。
    }
    return ans;
}

C++：

public:
    vector<vector<int>> levelOrder(TreeNode *root) {
        vector<vector<int>> ans;
        if (root == nullptr)
            return ans;
        queue<TreeNode *> q;// 创建队列
        q.push(root);// 把根节点添加到队列中
        while (!q.empty()) {
            int levelCount = q.size();// 每层的节点个数
            // 每层的集合。
            vector<int> subList;
            // 遍历当前层的所有节点，顺便把下一层的所有节点添加到队列中。
            for (int i = 0; i < levelCount; i++) {
                TreeNode *cur = q.front();
                q.pop();// 节点出队
                subList.push_back(cur->val);
                // 左右子节点如果不为空就添加到队列中。
                if (cur->left)
                    q.push(cur->left);
                if (cur->right)
                    q.push(cur->right);
            }
            ans.push_back(subList);// 当前层的集合添加到队列中。
        }
        return ans;
    }

C：

int **levelOrder(struct TreeNode *root, int *returnSize, int **returnColumnSizes) {
    *returnSize = 0;
    int **ans = (int **) malloc((sizeof(int *)) * 2001);
    if (root == NULL)
        return ans;
    *returnColumnSizes = malloc(sizeof(int) * 2001);
    struct TreeNode **q = (struct TreeNode **) malloc((sizeof(struct TreeNode *)) * 2001);// 创建队列
    int left = 0, right = 0;// 左闭右开
    q[right++] = root;// 把根节点添加到队列中
    while (left != right) {
        int levelCount = right - left;// 每层的节点个数
        // 每层的集合。
        int *subList = (int *) malloc((sizeof(int)) * levelCount);
        // 遍历当前层的所有节点，顺便把下一层的所有节点添加到队列中。
        for (int i = 0; i < levelCount; i++) {
            struct TreeNode *cur = q[left++];// 节点出队
            subList[i] = cur->val;
            // 左右子节点如果不为空就添加到队列中。
            if (cur->left)
                q[right++] = cur->left;
            if (cur->right)
                q[right++] = cur->right;
        }
        (*returnColumnSizes)[*returnSize] = levelCount;
        ans[(*returnSize)++] = subList;// 当前层的集合添加到队列中。
    }
    return ans;
}

Python：

def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
    ans = []
    if root is None:
        return ans
    q = deque([root])  # 创建队列
    while q:
        levelCount = len(q)  # 每层的节点个数
        # 每层的集合。
        subList = []
        # 遍历当前层的所有节点，顺便把下一层的所有节点添加到队列中。
        for _ in range(0, levelCount):
            cur = q.popleft()  # 节点出队
            subList.append(cur.val)
            # 左右子节点如果不为空就添加到队列中。
            if cur.left:
                q.append(cur.left)
            if cur.right:
                q.append(cur.right)
        ans.append(subList)  # 当前层的集合添加到队列中。
    return ans