暴躁的AI，国骂都学会了。。

精品推荐：

《征服数据结构》专栏：50多种数据结构彻底征服

《经典图论算法》专栏：50多种经典图论算法全部掌握

之前写过一篇文章《暴躁的AI，国骂都出来了》，结果有不少网友口味比较重，喜欢这种回答的方式，问我在哪找的，今天终于找到了，使用的是天工AI，下面是我让它回复的一个问题。

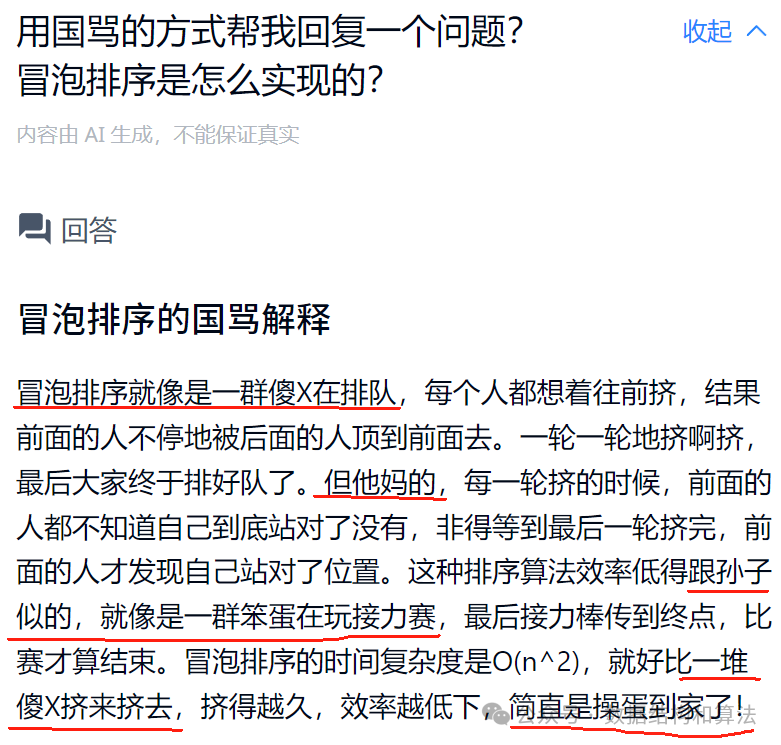
--------------下面是今天的算法题--------------

来看下今天的算法题，这题是LeetCode的第98：验证二叉搜索树。

问题描述

来源：LeetCode第98题

难度：中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

1，节点的左子树只包含小于当前节点的数。

2，节点的右子树只包含大于当前节点的数。

3，所有左子树和右子树自身必须也是二叉搜索树。

示例1：

输入：root = [2,1,3]

输出：true

示例2：

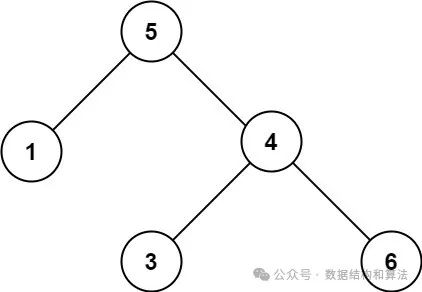
输入：root = [5,1,4,null,null,3,6]

输出：false

解释：根节点的值是 5 ，但是右子节点的值是 4 。

• 树中节点数目范围在[1, 10^4] 内

• -2^31 <= Node.val <= 2^31 - 1

问题分析

这题让验证二叉搜索树，二叉搜索树有一个规律就是它的中序遍历结果一定是有序的。我们只需要把这棵树按照中序遍历的顺序遍历，然后判断遍历的结果是否是有序的即可。

这里我们没必要全部遍历，按照中序遍历的方式每次和遍历的前一个节点比较，如果不是递增的，说明它不是二叉搜索树。

JAVA：

// 前一个结点
TreeNode prev;

public boolean isValidBST(TreeNode root) {
    if (root == null)
        return true;
    if (!isValidBST(root.left))// 递归左子树是否是二叉搜索树
        return false;

    // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点直接返回false。
    if (prev != null && prev.val >= root.val)
        return false;
    prev = root;

    // 递归右子树是否是二叉搜索树
    return isValidBST(root.right);
}

C++：

public:
    // 前一个结点
    TreeNode *prev;

    bool isValidBST(TreeNode *root) {
        if (root == nullptr)
            return true;
        if (!isValidBST(root->left))// 递归左子树是否是二叉搜索树
            return false;

        // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点直接返回false。
        if (prev && prev->val >= root->val)
            return false;
        prev = root;

        // 递归右子树是否是二叉搜索树
        return isValidBST(root->right);
    }

Python：

def isValidBST(self, root: Optional[TreeNode]) -> bool:
    prev = None  # 前一个结点

    def helper(node):
        nonlocal prev
        if node is None:
            return True
        if not helper(node.left):  # 递归左子树是否是二叉搜索树
            return False
        # 访问当前节点：如果当前节点小于等于中序遍历的前一个节点直接返回false。
        if prev is not None and prev.val >= node.val:
            return False
        prev = node
        # 递归右子树是否是二叉搜索树
        return helper(node.right)

    return helper(root)

笔者简介

博哥，真名：王一博，毕业十多年，《算法秘籍》作者，专注于数据结构和算法的讲解，在全球30多个算法网站中累计做题2000多道，在公众号中写算法题解800多题，对算法题有自己独特的解题思路和解题技巧，喜欢的可以给个关注，也可以下载我整理的1000多页的PDF算法文档。

《征服数据结构》专栏

数组，稀疏表(Sparse Table)，单向链表，双向链表，块状链表，跳表，队列和循环队列，双端队列，单调队列，栈，单调栈，双端栈，散列表，堆，字典树(Trie树)，ArrayMap，SparseArray，二叉树，二叉搜索树(BST)，笛卡尔树，AVL树，树堆(Treap)，FHQ-Treap

……

《经典图论算法》专栏

图的介绍，图的表示方式，邻接矩阵转换，广度优先搜索(BFS)，深度优先搜索(DFS)，A*搜索算法，迭代深化深度优先搜索(IDDFS)，IDA*算法，双向广度优先搜索，迪杰斯特拉算法(Dijkstra)，贝尔曼-福特算法(Bellman-Ford)，SPFA算法，弗洛伊德算法(Floyd)

……