重新思考推荐中的平均准确率指标优化-CSDN博客

TLDR:针对现有优化平均准确率方法存在的冗余和次优梯度分配问题，作者提出了一种新的损失来直接最小化每个正面实例之前的负面实例的数量。祝大家五四青年节快乐。

论文： https://ojs.aaai.org/index.php/AAAI/article/view/20042
代码： https://github.com/interestingzhuo/PNPloss

最近一些研究提出直接优化Average Precision (AP)来实现端到端的训练。尽管这些方法极大地促进了检索的发展，但是仍然存在两大问题。

(1) Redundancy exists in the optimization of AP.

这里，我们先给出的定义：

其中为排在正样本前面的正样本个数，为排在正样本前面的负样本个数。

如图所示，最小化AP等同于最小化，是因为只有当时，。因此计算是冗余的。

(2) Sub-optimal gradient assignment strategy.

如图1所示，基于AP的损失给较大的分配更小的梯度。然而不同的梯度分配策略会导致不同的性能。

针对第一个问题，作者提出了一种新的损失，即Penalizing Negative instances before Positive ones(PNP)，它直接最小化每个正面实例之前的负面实例的数量。

其中

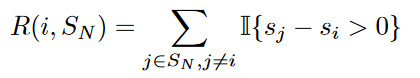
为了保证损失函数的可微性，作者利用sigmoid函数替代指示函数。其函数图像和导函数图像如图3(a)所示。

针对第二个问题，作者提出了多种PNP的变体。其中有PNP-Increasing (PNP-I) with increasing derivative functions and PNP-Decreasing (PNP-D) with decreasing ones.

不失一般性，作者将PNP-I分为 with unbounded derivative function 和 with bounded derivative functions.

其中的导函数和损失函数如下：

可以看出，当损失为0时，导函数也将为0；当函数趋于无穷时，导函数也趋于无穷。另外，并未增加额外的参数，因此并未增加训练的困难。其函数图像和导函数图像如图3(b)所示。

的导函数和损失函数如下：

参数b为一个可调的边界值。其函数图像和导函数图像如图3(c)所示。

同样，作者提出了两种导函数 with slow speed 和 with fast speed. 其函数和导函数如下所示：

这两个函数的导数函数都是递减的，这意味着有较少负样本排在前面的正样本会受到更多的惩罚，这两个损失函数会迅速纠正这种情况。

PNP-I对于排名前有较多负样本的正样本的梯度越大，而PNP-D对该类正样本的梯度越小。PNP-I尝试将所有相关样本放在一起。相比之下，PNP-D只会快速纠正排名前负样本个数较少的正样本，因为这样的样本被认为与query属于同一个中心。

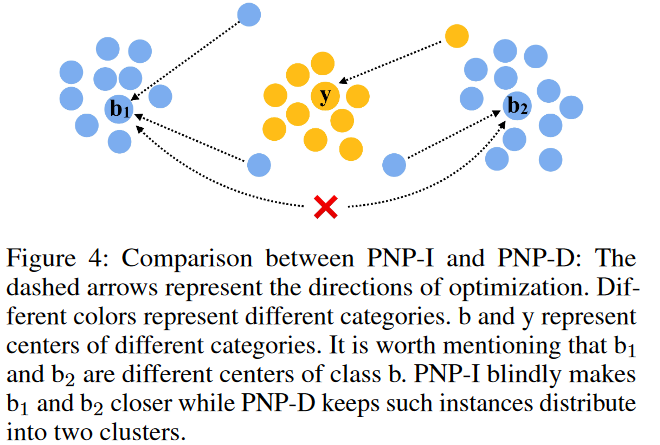
如图4所示，若和在同一个batch里被采样到，则PNP-I会分配更大的权重给和，从而使得和距离更近。相反，考虑到和之间有较多的负样本，PNP-D会分配较小的梯度，并为蓝色类保留多中心分布。

AP关于的导函数如下，

其函数图像如图5所示

从图中可以看出，AP与PNP-D有着相似的梯度曲线。然而，当有太多正样本排在目标正样本前时，对于不同的，其梯度几乎相同。这说明当考虑排在目标正样本前的正样本数目时会削弱梯度优势，从而降低检索性能。

-- Recall@k

-- dists@intra (Mean Intraclass Distance)

-- dists@inter (Mean Interclass Distance)

-- Normalized Mutual Information (NMI)

可以看出，PNP-D一致优于PNP-O和PNP-I。并且，PNP-D相比于PNP-I有更大的dist@intra，dists@inter和NMI，因此有着更好的泛化性。如图6所示，PNP-I难以将测试集中的类别区分开，而PNP-D可以。

实验表明，PNP-D展现出了优异的性能。

更多实验及其相关细节参考原文。

在本文中，作者提出了一种新的PNP损失，它通过惩罚排在正样本之前的负样本来提高检索性能。此外，作者发现不同损失的导数函数对应不同的梯度赋值。因此，通过构造损失的导数函数，系统地研究了不同的梯度赋值解，得到了PNP-I和PNP-D。PNP-D在三个基准数据集上始终实现最先进的性能。