火鹰优化算法优化支持向量机原理及MATLAB代码构建-CSDN博客

本文链接：https://blog.csdn.net/2403_88401503/article/details/147901192

0 引言

火鹰优化算法（Fire Hawk Optimizer，FHO）是由Mahdi Azizi等人于2022年提出。该算法是模拟火鹰为了控制和捕获猎物，捡起燃烧的木棍并将其丢弃在其他未燃烧的地方，以点燃小火堆，吓跑了待捕猎物，迫使它们以仓促和紧张的方式逃跑，从而更容易被鹰捕捉。如下图所示

1 数学模型

FHO算法的数学模型构建围绕火鹰的觅食行为，同时考虑了火鹰的取火、散火、捕食和猎物移动的过程，其具体模型构建如下：

1）初始化火鹰位置和选择搜索维度空间：确定若干个解候选(X)，作为火鹰和猎物的位置向量。通过随机初始化过程来确定这些向量在搜索空间中的初始位置。具体表达式如下式所示：

其中Xi表示搜索空间中的第i个解候选；d表示所考虑问题的维度；N是搜索空间中解候选的总数；x_j_i是第i个解候选的第j个决策变量，xmin和xmax分别是第i个解候选的第j个决策变量的最小值和最大值；rand是在[0,1]范围内均匀分布的随机数

2）区分火鹰和猎物：为了确定火鹰在搜索空间中的位置，用于在搜索空间中围绕猎物和传播食物选定为火鹰，其余为猎物，具体表达式如下式所示，其围绕猎物和传播食物图如下：

其中PRk是搜索空间中第k个猎物相对于总猎物数m而言；FHi是搜索空间中第l个自由鹰相对于总自由鹰数n而言。这些值选自上述初始向量。

3）确定火鹰和猎物之间总距离：确定具有最佳目标函数值的火鹰最近的猎物，从而进行捕猎，而其他火鹰的领地则通过剩余的猎物来考虑，具体表达式如下式所示：

其中Dl_k是第l只猎鹰与第k只猎物之间的总距离；m是搜索空间中猎物的总数；n是搜索空间中猎鹰的总数；x和y表示搜索空间中猎鹰和猎物的向量。

4）散布火焰：火鹰会到主火位置或者附近其他火鹰领地内取火并返回自己的领地散布火焰，以此让自己领地内的猎物受惊逃窜，便于达到更好捕猎的目的，具体表达式如下式所示：

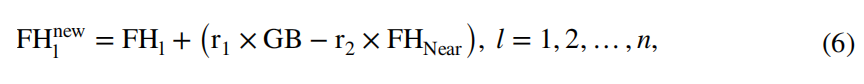
其中，FHnew l是第l只火鹰（FHl）的新位置向量；GB是搜索空间中的全局最优解；FHnear是搜索空间中的另一只火鹰；r1和r2是在（0,1）范围内均匀分布的随机数。

5）猎物移动：当火鹰掉落燃烧的木棍时，猎物会决定隐藏、逃跑或误以为火鹰在向它们跑来。这些行为可以通过以下方程在位置更新过程中考虑：具体表达式如下式所示：

其中，PRnew q是第q只猎物（PRq）被第l只火鹰（FHl）包围的新位置向量，SPl是第l只火鹰领地下的安全区域；r3和r4是在（0,1）范围内均匀分布的随机数，此外，猎物还可能向其他火鹰的领地移动，如式8所示。基于自然中的安全地点是大多数动物为了在危险中保持安全而聚集的地方，SPl和SP的数学表述如下：

2 优化方式

前篇对支持向量机（支持向量机原理及MATLAB代码复现_matlab 支持向量机-CSDN博客）原理讲解，从支持向量机模型运算过程中，可以了解到模型高维映射核函数参数g和处罚因子c对模型预测结果影响最为重要。因此结合上述FHO原理介绍，可以将支持向量机的超参数作为火鹰和猎物个体位置，每一个位置对应支持向量机的预测值，将这个预测值作为适应度作为火鹰和猎物距离位置，模拟上述行为达到收敛状态。

3 MATLAB代码

3.1 伪代码

出自原作者发表期刊。

3.2 主函数代码

%%MATLAB火鹰优化算法主函数
for i=1:nPop
    % 初始化种群
    Pop(i,:)=unifrnd(VarMin,VarMax,[1 VarNumber]);
    
    % 初始化适应度
    Cost(i,1)=SYD(Pop(i,:),net);
    net.trainParam.showWindow = 0;
    FEs=FEs+1;
end
% 种群排序
[Cost, SortOrder]=sort(Cost);
Pop=Pop(SortOrder,:);
BestPop=Pop(1,:);
SP=mean(Pop);

% 火鹰
FHPops=Pop(1:HN,:);

% 猎物
Pop2=Pop(HN+1:end,:);

% 火鹰与猎物之间的距离
for i=1:HN
    nPop2=size(Pop2,1);
    if nPop2<HN
        break
    end
    Dist=[];
    for q=1:nPop2
        Dist(q,1)=distance(FHPops(i,:), Pop2(q,:));

    end
    [ ~, b]=sort(Dist);
    alfa=randi(nPop2);
    PopNew{i,:}=Pop2(b(1:alfa),:);
    Pop2(b(1:alfa),:)=[];

    if isempty(Pop2)==1
        break
    end
end
if isempty(Pop2)==0

    PopNew{end,:}=[PopNew{end,:} ;Pop2];

end

% 更新最佳
GB=Cost(1);
BestPos=BestPop;

%% 开始
while FEs < MaxFes
    Iter=Iter+1;
    PopTot=[];
    Cost=[];
    for i=1:size(PopNew,1)
        PR=cell2mat(PopNew(i));
        FHl=FHPops(i,:);
        SPl=mean(PR);
        
        Ir=unifrnd(0,1,1,2);
        FHnear=FHPops(randi(HN),:);
        FHl_new=FHl+(Ir(1)*GB-Ir(2)*FHnear);
        FHl_new = max(FHl_new,VarMin);
        FHl_new = min(FHl_new,VarMax);
        PopTot=[PopTot ;FHl_new];
        
        for q=1:size(PR,1)
            
            Ir=unifrnd(0,1,1,2);
            PRq_new1=PR(q,:)+((Ir(1)*FHl-Ir(2)*SPl));
            PRq_new1 = max(PRq_new1,VarMin);
            PRq_new1 = min(PRq_new1,VarMax);
            PopTot=[PopTot ;PRq_new1];
            
            Ir=unifrnd(0,1,1,2);
            FHAlter=FHPops(randi(HN),:);
            PRq_new2=PR(q,:)+((Ir(1)*FHAlter-Ir(2)*SP));
            PRq_new2 = max(PRq_new2,VarMin);
            PRq_new2 = min(PRq_new2,VarMax);
            PopTot=[PopTot ;PRq_new2];
        end
    end
    for i=1:size(PopTot,1)
        Cost(i,1)=SYD(PopTot(i,:),net);
        net.trainParam.showWindow = 0;       
    end
   % 种群排列
    [Cost, SortOrder]=sort(Cost);
    PopTot=PopTot(SortOrder,:);
    Pop=PopTot(1:nPop,:);

    HN = randi([1 ceil(nPop/5)],1,1);

    BestPop=Pop(1,:);
    SP=mean(Pop);
    FHPops=Pop(1:HN,:);
    Pop2=Pop(HN+1:end,:);
    clear PopNew
    
    % 火鹰与猎物之间的距离
    for i=1:HN
        nPop2=size(Pop2,1);
        if nPop2<HN
            break
        end
        Dist=[];
        for q=1:nPop2
            Dist(q,1)=distance(FHPops(i,:), Pop2(q,:));
        end
        [ ~, b]=sort(Dist);
        alfa=randi(nPop2);
        PopNew{i,:}=Pop2(b(1:alfa),:);
        Pop2(b(1:alfa),:)=[];
        if isempty(Pop2)==1
            break
        end
    end

    if isempty(Pop2)==0
        PopNew{end,:}=[PopNew{end,:} ;Pop2];
    end

    % 更新最佳适应度
    if Cost(1)<GB
        BestPos=BestPop;
    end
    GB=min(GB,Cost(1));
    
    BestCosts(Iter)=GB;
    FEs = FEs+1;
    Conv_History(FEs)=GB;
    
end